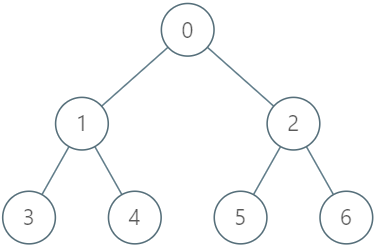
给你一棵 n 个节点的树,编号从 0 到 n - 1 ,以父节点数组 parent 的形式给出,其中 parent[i] 是第 i 个节点的父节点。树的根节点为 0 号节点,所以 parent[0] = -1 ,因为它没有父节点。你想要设计一个数据结构实现树里面对节点的加锁,解锁和升级操作。
数据结构需要支持如下函数:
- Lock:指定用户给指定节点 上锁 ,上锁后其他用户将无法给同一节点上锁。只有当节点处于未上锁的状态下,才能进行上锁操作。
- Unlock:指定用户给指定节点 解锁 ,只有当指定节点当前正被指定用户锁住时,才能执行该解锁操作。
- Upgrade:指定用户给指定节点 上锁 ,并且将该节点的所有子孙节点 解锁 。只有如下 3 个条件 全部 满足时才能执行升级操作:
- 指定节点当前状态为未上锁。
- 指定节点至少有一个上锁状态的子孙节点(可以是 任意 用户上锁的)。
- 指定节点没有任何上锁的祖先节点。
请你实现 LockingTree 类:
LockingTree(int[] parent)用父节点数组初始化数据结构。lock(int num, int user)如果 id 为user的用户可以给节点num上锁,那么返回true,否则返回false。如果可以执行此操作,节点num会被 id 为user的用户 上锁 。unlock(int num, int user)如果 id 为user的用户可以给节点num解锁,那么返回true,否则返回false。如果可以执行此操作,节点num变为 未上锁 状态。upgrade(int num, int user)如果 id 为user的用户可以给节点num升级,那么返回true,否则返回false。如果可以执行此操作,节点num会被 升级 。
示例 1:
输入:
["LockingTree", "lock", "unlock", "unlock", "lock", "upgrade", "lock"]
[[[-1, 0, 0, 1, 1, 2, 2]], [2, 2], [2, 3], [2, 2], [4, 5], [0, 1], [0, 1]]
输出:
[null, true, false, true, true, true, false]
解释:
LockingTree lockingTree = new LockingTree([-1, 0, 0, 1, 1, 2, 2]);
lockingTree.lock(2, 2); // 返回 true ,因为节点 2 未上锁。
// 节点 2 被用户 2 上锁。
lockingTree.unlock(2, 3); // 返回 false ,因为用户 3 无法解锁被用户 2 上锁的节点。
lockingTree.unlock(2, 2); // 返回 true ,因为节点 2 之前被用户 2 上锁。
// 节点 2 现在变为未上锁状态。
lockingTree.lock(4, 5); // 返回 true ,因为节点 4 未上锁。
// 节点 4 被用户 5 上锁。
lockingTree.upgrade(0, 1); // 返回 true ,因为节点 0 未上锁且至少有一个被上锁的子孙节点(节点 4)。
// 节点 0 被用户 1 上锁,节点 4 变为未上锁。
lockingTree.lock(0, 1); // 返回 false ,因为节点 0 已经被上锁了。
提示:
n == parent.length2 <= n <= 2000- 对于
i != 0,满足0 <= parent[i] <= n - 1 parent[0] == -10 <= num <= n - 11 <= user <= 104parent表示一棵合法的树。lock,unlock和upgrade的调用 总共 不超过2000次。
方法一:哈希表 + DFS
class LockingTree:
def __init__(self, parent: List[int]):
self.nums = {}
self.parent = parent
self.children = defaultdict(list)
for i, p in enumerate(parent):
self.children[p].append(i)
def lock(self, num: int, user: int) -> bool:
if num in self.nums:
return False
self.nums[num] = user
return True
def unlock(self, num: int, user: int) -> bool:
if num not in self.nums or self.nums[num] != user:
return False
self.nums.pop(num)
return True
def upgrade(self, num: int, user: int) -> bool:
def dfs(num):
nonlocal find
for child in self.children[num]:
if child in self.nums:
self.nums.pop(child)
find = True
dfs(child)
t = num
while t != -1:
if t in self.nums:
return False
t = self.parent[t]
find = False
dfs(num)
if not find:
return False
self.nums[num] = user
return True
# Your LockingTree object will be instantiated and called as such:
# obj = LockingTree(parent)
# param_1 = obj.lock(num,user)
# param_2 = obj.unlock(num,user)
# param_3 = obj.upgrade(num,user)class LockingTree {
private Map<Integer, Integer> nums;
private int[] parent;
private List<Integer>[] children;
public LockingTree(int[] parent) {
nums = new HashMap<>();
this.parent = parent;
int n = parent.length;
children = new List[n];
for (int i = 0; i < n; ++i) {
children[i] = new ArrayList<>();
}
for (int i = 0; i < n; ++i) {
if (parent[i] != -1) {
children[parent[i]].add(i);
}
}
}
public boolean lock(int num, int user) {
if (nums.containsKey(num)) {
return false;
}
nums.put(num, user);
return true;
}
public boolean unlock(int num, int user) {
if (!nums.containsKey(num) || nums.get(num) != user) {
return false;
}
nums.remove(num);
return true;
}
public boolean upgrade(int num, int user) {
int t = num;
while (t != -1) {
if (nums.containsKey(t)) {
return false;
}
t = parent[t];
}
boolean[] find = new boolean[1];
dfs(num, find);
if (!find[0]) {
return false;
}
nums.put(num, user);
return true;
}
private void dfs(int num, boolean[] find) {
for (int child : children[num]) {
if (nums.containsKey(child)) {
nums.remove(child);
find[0] = true;
}
dfs(child, find);
}
}
}
/**
* Your LockingTree object will be instantiated and called as such:
* LockingTree obj = new LockingTree(parent);
* boolean param_1 = obj.lock(num,user);
* boolean param_2 = obj.unlock(num,user);
* boolean param_3 = obj.upgrade(num,user);
*/class LockingTree {
public:
unordered_map<int, int> nums;
vector<int> parent;
vector<vector<int>> children;
LockingTree(vector<int>& parent) {
this->parent = parent;
int n = parent.size();
children.resize(n);
for (int i = 0; i < n; ++i)
if (parent[i] != -1)
children[parent[i]].push_back(i);
}
bool lock(int num, int user) {
if (nums.count(num)) return false;
nums[num] = user;
return true;
}
bool unlock(int num, int user) {
if (!nums.count(num) || nums[num] != user) return false;
nums.erase(num);
return true;
}
bool upgrade(int num, int user) {
for (int t = num; t != -1; t = parent[t])
if (nums.count(t))
return false;
bool find = false;
dfs(num, find);
if (!find) return false;
nums[num] = user;
return true;
}
void dfs(int num, bool& find) {
for (int child : children[num]) {
if (nums.count(child)) {
nums.erase(child);
find = true;
}
dfs(child, find);
}
}
};
/**
* Your LockingTree object will be instantiated and called as such:
* LockingTree* obj = new LockingTree(parent);
* bool param_1 = obj->lock(num,user);
* bool param_2 = obj->unlock(num,user);
* bool param_3 = obj->upgrade(num,user);
*/type LockingTree struct {
nums map[int]int
parent []int
children [][]int
}
func Constructor(parent []int) LockingTree {
n := len(parent)
nums := make(map[int]int)
children := make([][]int, n)
for i, p := range parent {
if p != -1 {
children[p] = append(children[p], i)
}
}
return LockingTree{nums, parent, children}
}
func (this *LockingTree) Lock(num int, user int) bool {
if _, ok := this.nums[num]; ok {
return false
}
this.nums[num] = user
return true
}
func (this *LockingTree) Unlock(num int, user int) bool {
if this.nums[num] != user {
return false
}
delete(this.nums, num)
return true
}
func (this *LockingTree) Upgrade(num int, user int) bool {
for t := num; t != -1; t = this.parent[t] {
if _, ok := this.nums[t]; ok {
return false
}
}
find := false
var dfs func(int)
dfs = func(num int) {
for _, child := range this.children[num] {
if _, ok := this.nums[child]; ok {
delete(this.nums, child)
find = true
}
dfs(child)
}
}
dfs(num)
if !find {
return false
}
this.nums[num] = user
return true
}
/**
* Your LockingTree object will be instantiated and called as such:
* obj := Constructor(parent);
* param_1 := obj.Lock(num,user);
* param_2 := obj.Unlock(num,user);
* param_3 := obj.Upgrade(num,user);
*/