There is an undirected tree with n nodes labeled from 0 to n - 1, rooted at node 0. You are given a 2D integer array edges of length n - 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.
At every node i, there is a gate. You are also given an array of even integers amount, where amount[i] represents:
- the price needed to open the gate at node
i, ifamount[i]is negative, or, - the cash reward obtained on opening the gate at node
i, otherwise.
The game goes on as follows:
- Initially, Alice is at node
0and Bob is at nodebob. - At every second, Alice and Bob each move to an adjacent node. Alice moves towards some leaf node, while Bob moves towards node
0. - For every node along their path, Alice and Bob either spend money to open the gate at that node, or accept the reward. Note that:
- If the gate is already open, no price will be required, nor will there be any cash reward.
- If Alice and Bob reach the node simultaneously, they share the price/reward for opening the gate there. In other words, if the price to open the gate is
c, then both Alice and Bob payc / 2each. Similarly, if the reward at the gate isc, both of them receivec / 2each.
- If Alice reaches a leaf node, she stops moving. Similarly, if Bob reaches node
0, he stops moving. Note that these events are independent of each other.
Return the maximum net income Alice can have if she travels towards the optimal leaf node.
Example 1:
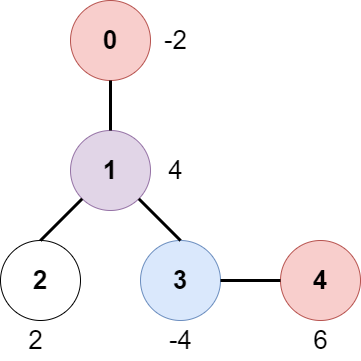
Input: edges = [[0,1],[1,2],[1,3],[3,4]], bob = 3, amount = [-2,4,2,-4,6] Output: 6 Explanation: The above diagram represents the given tree. The game goes as follows: - Alice is initially on node 0, Bob on node 3. They open the gates of their respective nodes. Alice's net income is now -2. - Both Alice and Bob move to node 1. Since they reach here simultaneously, they open the gate together and share the reward. Alice's net income becomes -2 + (4 / 2) = 0. - Alice moves on to node 3. Since Bob already opened its gate, Alice's income remains unchanged. Bob moves on to node 0, and stops moving. - Alice moves on to node 4 and opens the gate there. Her net income becomes 0 + 6 = 6. Now, neither Alice nor Bob can make any further moves, and the game ends. It is not possible for Alice to get a higher net income.
Example 2:
Input: edges = [[0,1]], bob = 1, amount = [-7280,2350] Output: -7280 Explanation: Alice follows the path 0->1 whereas Bob follows the path 1->0. Thus, Alice opens the gate at node 0 only. Hence, her net income is -7280.
Constraints:
2 <= n <= 105edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != biedgesrepresents a valid tree.1 <= bob < namount.length == namount[i]is an even integer in the range[-104, 104].
class Solution:
def mostProfitablePath(self, edges: List[List[int]], bob: int, amount: List[int]) -> int:
def dfs1(i, fa, t):
if i == 0:
ts[i] = min(ts[i], t)
return True
for j in g[i]:
if j != fa and dfs1(j, i, t + 1):
ts[j] = min(ts[j], t + 1)
return True
return False
def dfs2(i, fa, t, v):
if t == ts[i]:
v += amount[i] // 2
elif t < ts[i]:
v += amount[i]
nonlocal ans
if len(g[i]) == 1 and g[i][0] == fa:
ans = max(ans, v)
return
for j in g[i]:
if j != fa:
dfs2(j, i, t + 1, v)
n = len(edges) + 1
g = defaultdict(list)
ts = [n] * n
for a, b in edges:
g[a].append(b)
g[b].append(a)
dfs1(bob, -1, 0)
ts[bob] = 0
ans = -inf
dfs2(0, -1, 0, 0)
return ansclass Solution {
private List<Integer>[] g;
private int[] amount;
private int[] ts;
private int ans = Integer.MIN_VALUE;
public int mostProfitablePath(int[][] edges, int bob, int[] amount) {
int n = edges.length + 1;
g = new List[n];
ts = new int[n];
this.amount = amount;
for (int i = 0; i < n; ++i) {
g[i] = new ArrayList<>();
ts[i] = n;
}
for (var e : edges) {
int a = e[0], b = e[1];
g[a].add(b);
g[b].add(a);
}
dfs1(bob, -1, 0);
ts[bob] = 0;
dfs2(0, -1, 0, 0);
return ans;
}
private boolean dfs1(int i, int fa, int t) {
if (i == 0) {
ts[i] = Math.min(ts[i], t);
return true;
}
for (int j : g[i]) {
if (j != fa && dfs1(j, i, t + 1)) {
ts[j] = Math.min(ts[j], t + 1);
return true;
}
}
return false;
}
private void dfs2(int i, int fa, int t, int v) {
if (t == ts[i]) {
v += amount[i] >> 1;
} else if (t < ts[i]) {
v += amount[i];
}
if (g[i].size() == 1 && g[i].get(0) == fa) {
ans = Math.max(ans, v);
return;
}
for (int j : g[i]) {
if (j != fa) {
dfs2(j, i, t + 1, v);
}
}
}
}class Solution {
public:
int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {
int n = edges.size() + 1;
vector<vector<int>> g(n);
for (auto& e : edges) {
int a = e[0], b = e[1];
g[a].emplace_back(b);
g[b].emplace_back(a);
}
vector<int> ts(n, n);
function<bool(int i, int fa, int t)> dfs1 = [&](int i, int fa, int t) -> bool {
if (i == 0) {
ts[i] = t;
return true;
}
for (int j : g[i]) {
if (j != fa && dfs1(j, i, t + 1)) {
ts[j] = min(ts[j], t + 1);
return true;
}
}
return false;
};
dfs1(bob, -1, 0);
ts[bob] = 0;
int ans = INT_MIN;
function<void(int i, int fa, int t, int v)> dfs2 = [&](int i, int fa, int t, int v) {
if (t == ts[i]) v += amount[i] >> 1;
else if (t < ts[i]) v += amount[i];
if (g[i].size() == 1 && g[i][0] == fa) {
ans = max(ans, v);
return;
}
for (int j : g[i]) if (j != fa) dfs2(j, i, t + 1, v);
};
dfs2(0, -1, 0, 0);
return ans;
}
};func mostProfitablePath(edges [][]int, bob int, amount []int) int {
n := len(edges) + 1
g := make([][]int, n)
for _, e := range edges {
a, b := e[0], e[1]
g[a] = append(g[a], b)
g[b] = append(g[b], a)
}
ts := make([]int, n)
for i := range ts {
ts[i] = n
}
var dfs1 func(int, int, int) bool
dfs1 = func(i, fa, t int) bool {
if i == 0 {
ts[i] = min(ts[i], t)
return true
}
for _, j := range g[i] {
if j != fa && dfs1(j, i, t+1) {
ts[j] = min(ts[j], t+1)
return true
}
}
return false
}
dfs1(bob, -1, 0)
ts[bob] = 0
ans := -0x3f3f3f3f
var dfs2 func(int, int, int, int)
dfs2 = func(i, fa, t, v int) {
if t == ts[i] {
v += amount[i] >> 1
} else if t < ts[i] {
v += amount[i]
}
if len(g[i]) == 1 && g[i][0] == fa {
ans = max(ans, v)
return
}
for _, j := range g[i] {
if j != fa {
dfs2(j, i, t+1, v)
}
}
}
dfs2(0, -1, 0, 0)
return ans
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
func max(a, b int) int {
if a > b {
return a
}
return b
}