TODO 样条

Aglargil · Dec 29, 2024 · 1f8958f · 1f8958f
1 parent cb48e3b
commit 1f8958f
Show file tree

Hide file tree

Showing 2 changed files with 29 additions and 11 deletions.
diff --git a/docs/blog/posts/样条.md b/docs/blog/posts/样条.md
diff --git a/docs/blog/tmp/样条.md b/docs/blog/tmp/样条.md
@@ -0,0 +1,29 @@
+---
+title: 样条
+date:
+  created: 2024-12-21
+  updated: 2024-12-21
+categories:
+  - 数学
+---
+
+!!! quote 
+    本文主要内容参考自 [The Continuity of Splines](https://www.youtube.com/watch?v=jvPPXbo87ds&t=2037s)
+
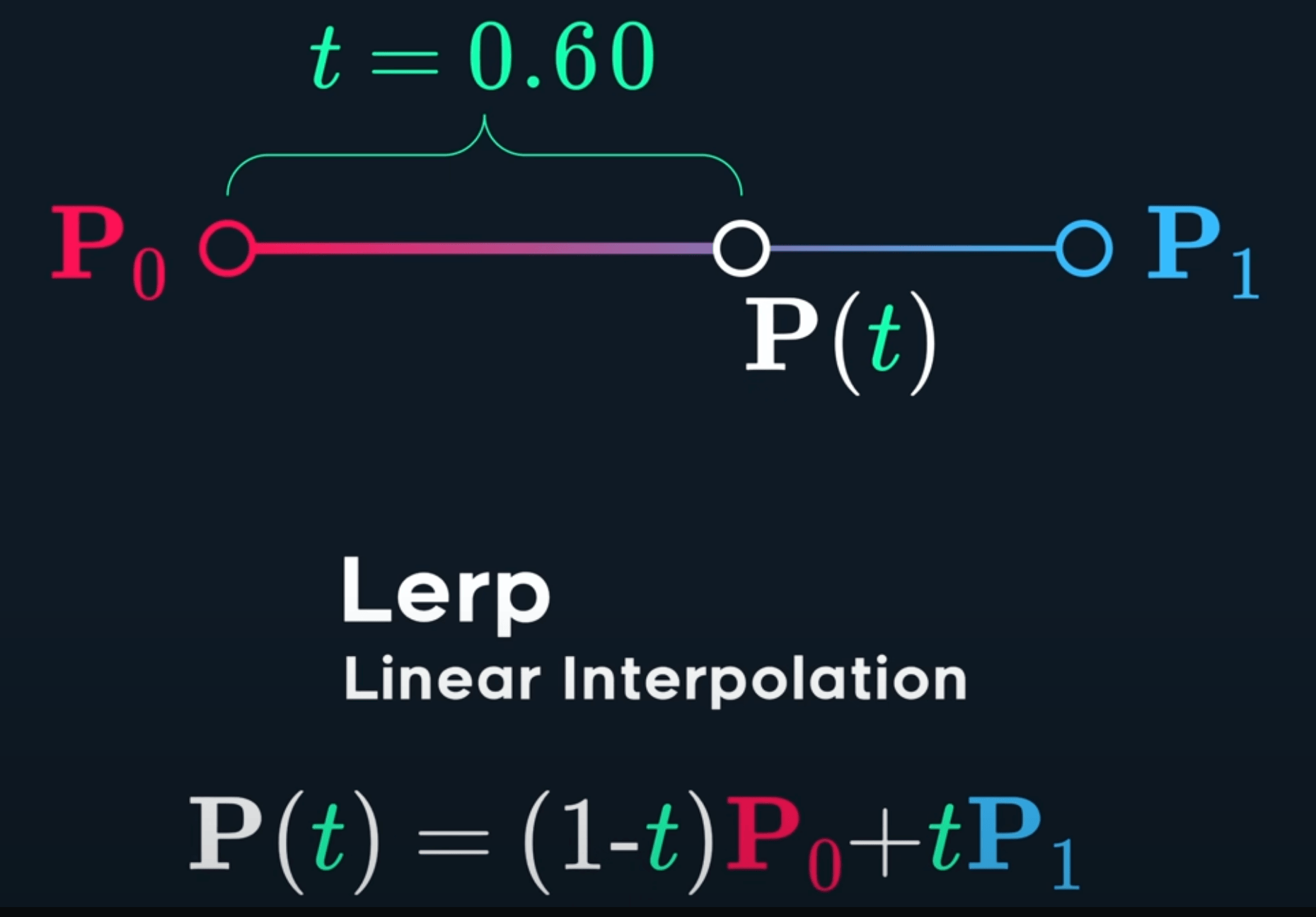
+## 0. 线性插值(Lerp / Linear Interpolation)
+
+![](https://picgo-1257309505.cos.ap-guangzhou.myqcloud.com/20241221180341882.png?imageSlim)
+
+<!-- more -->
+
+Lerp: $Lerp(a, b, t) = (1-t)a + tb$
+
+
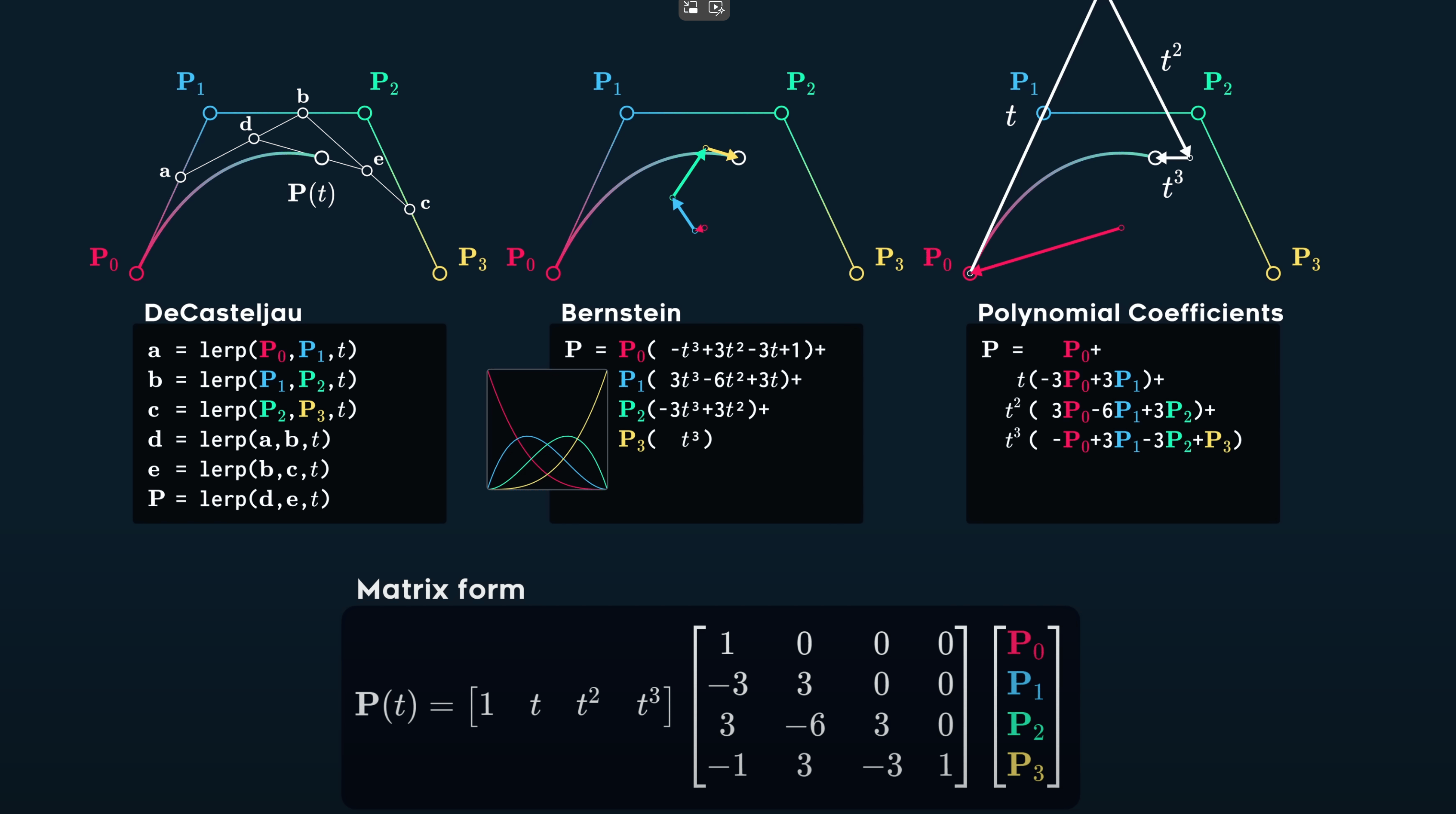
+## 1. 贝塞尔曲线(Bézier Curve)
+
+假设有三个点 $P_0, P_1, P_2$，我们分别对$P_0$和$P_1$进行线性插值，对$P_1$和$P_2$进行线性插值，然后再对这两个结果进行线性插值，得到的结果就是二阶贝塞尔曲线上的点。
+
+即 $B(t) = Lerp(Lerp(P_0, P_1, t), Lerp(P_1, P_2, t), t)$
+
+### 1.1 贝塞尔曲线的表示方式
+![](https://picgo-1257309505.cos.ap-guangzhou.myqcloud.com/20241221181820825.png?imageSlim)