https://blog.jiangyayu.cn/archives/linear-equation.html/
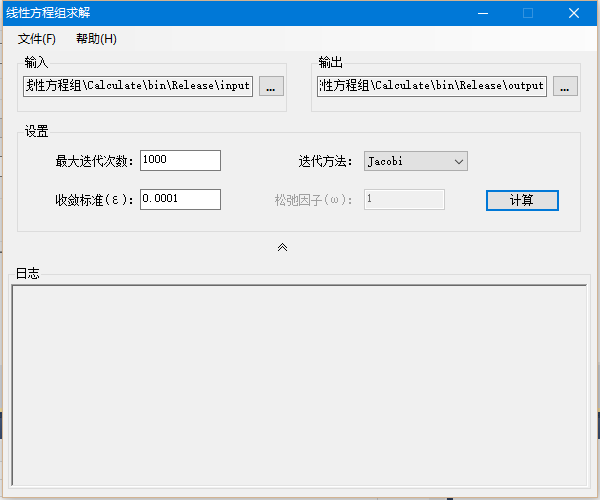
应用程序包含菜单、输入输出、设置和日志模块,如图所示:
- 路径说明
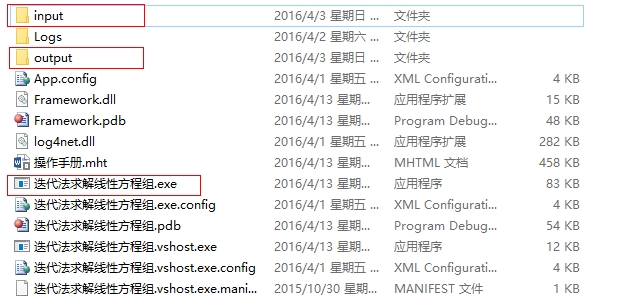
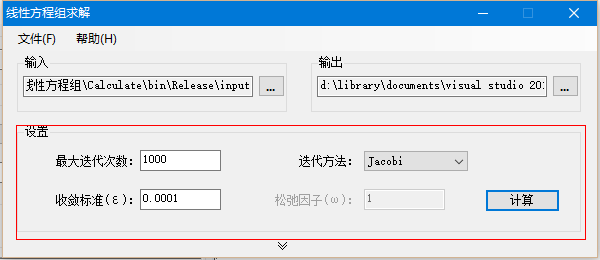
程序启动时,会自动读取所在路径,默认的输入输出路径为应用程序目录下的input和output文件夹(下图所示)。程序计算所需的输入数据存应存放于input文件夹中,最终计算结果将输出到output文件夹中。 也可以通过修改输入输出路径的方法,重新指定输入数据存放的位置和最终计算结果的输出位置。
- 数据格式
(1)输入数据
位于应用程序所在路径下的input文件夹的.txt文本文件,其数据格式为:
第一行为线性方程组的未知数个数; 第二行起的数据代表线性方程组系数的增广矩阵,每一行表示一个线性方程。
(2)输出结果 位于应用程序所在路径下的output文件夹的.txt文本文件,其数据格式为: 从第一行开始分别表示线性方程组的解x1,x2,x3,…的值,最后两行分别标识所使用迭代方法和迭代次数。
如图所示部分为迭代求解过程中的参数数值的设定,
最大迭代次数: 指示迭代过程中,最大迭代的次数。迭代次数超过该值时停止迭代。
收敛标准(ε): 当两次迭代所得数值之差的绝对值均小于某一给定的数ε时,视为已求得近似解。此时停止迭代,输出结果。
( 注: 以上条件满足其一,即停止迭代。)
迭代方法: 求解使用的迭代方法。该程序内置迭代方法有:Jacobi迭代法、Gauss-Seidel迭代法、逐次超松弛迭代法(SOR法)。
松弛因子(ω): SOR迭代法的参数,一般1<ω<2;
0<ω<1时,称为亚松弛法;
ω > 1时,称为超松弛法;
Ω=1时,即为高斯-塞德尔迭代;
(1) 应用程序会遍历输入文件夹中的所有.txt文件,按照指定的数据格式读取文件
读取的输入文件格式为:
第一行为线性方程组的未知数个数; 第二行起的数据代表线性方程组系数的增广矩阵,每一行表示一个线性方程。
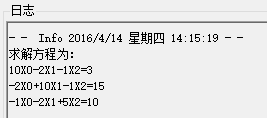
(2) 可以根据文件内容生成并显示方程
(3) 根据指定的参数和迭代方法求解方程组
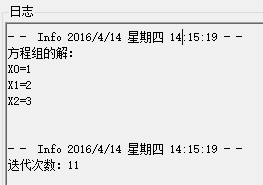
(4) 显示求解结果
(5) 将最终结果存放至输出文件夹中,并命名为xxx_solution.txt
从第一行开始分别表示线性方程组的解x1,x2,x3,…的值,最后两行分别标识所使用迭代方法和迭代次数。
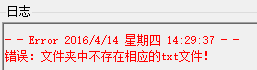
(1) 路径错误
(2) 文件为空
(3) 数据内容错误
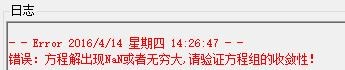
(4) 解不收敛
迭代部分的源码:
/// <summary>
/// 方程组系数增广矩阵等价变换
/// </summary>
/// <param name="c">输入增广矩阵</param>
/// <returns>等价变换后的增广矩阵</returns>
private static List<double[]> matTrans(List<double[]> c)
{
List<double[]> cTrans = new List<double[]>();
for (int i = 0; i < c.Count; i++)
{
double[] ci = new double[c[i].Length];
c[i].CopyTo(ci, 0);
if (ci[i] == 0)
{
ci = c[i];
ci[i] = 1;
ci[ci.Length - 1] = -ci[ci.Length - 1];
}
else
{
for (int j = 0; j < ci.Length ; j++)
{
ci[j] = -ci[j] / c[i][i];
}
ci[i] = 0;
ci[ci.Length - 1] = -ci[ci.Length - 1];
}
cTrans.Add(ci);
}
return cTrans;
}
/// <summary>
/// Jacobi迭代法求解线性方程组
/// </summary>
/// <param name="c">方程组系数的增广矩阵</param>
/// <param name="IterativeTimes">最大迭代次数</param>
/// <param name="Epsilon">收敛标准</param>
/// <param name="t">迭代次数</param>
/// <param name="solution">求解结果</param>
/// <returns>执行结果,0表示求解成功</returns>
public static int Jacobi(List<double[]> c, int IterativeTimes, double Epsilon, out int t, double[] solution)
{
List<double[]> cTrans = matTrans(c);
double[] history = new double[cTrans.Count];
double[] now = new double[cTrans.Count];
int times = 0;
bool isTrueSolution = false;
while (times <= IterativeTimes && !isTrueSolution)
{
//迭代一次
for (int i = 0; i < cTrans.Count; i++)
{
now[i] = 0;
double[] Con = cTrans[i];
for (int j = 0; j < Con.Length - 1; j++)
{
now[i] += Con[j] * history[j];
}
now[i] += Con[Con.Length - 1];
if (Double.IsNaN(now[i]) || Double.IsInfinity(now[i]))
throw new Exception("错误:方程解出现NaN或者无穷大,请验证方程组的收敛性!");
}
times++;
//解是否符合条件
isTrueSolution = true;
for (int i = 0; i < now.Length; i++)
{
if (Math.Abs(now[i] - history[i]) > Epsilon)
{
isTrueSolution = false;
break;
}
}
//更新旧解
now.CopyTo(history, 0);
}
t = times;
now.CopyTo(solution, 0);
//超出迭代次数求解失败
if (times > IterativeTimes) return 1;
else
return 0;
}
/// <summary>
/// SOR迭代法求解线性方程组
/// </summary>
/// <param name="c">方程组系数的增广矩阵</param>
/// <param name="IterativeTimes">最大迭代次数</param>
/// <param name="Epsilon">收敛标准</param>
/// <param name="omega">松弛因子</param>
/// <param name="t">迭代次数</param>
/// <param name="solution">求解结果</param>
/// <returns>执行结果,0表示求解成功</returns>
public static int SOR(List<double[]> c, int IterativeTimes, double Epsilon,double omega, out int t, double[] solution)
{
List<double[]> cTrans = matTrans(c);
double[] history = new double[cTrans.Count];
double[] now = new double[cTrans.Count];
int times = 0;
bool isTrueSolution = false;
while (times <= IterativeTimes && !isTrueSolution)
{ //一次迭代
for (int i = 0; i < cTrans.Count; i++)
{
now.CopyTo(history, 0);
now[i] = (1-omega)*history[i];
double[] Con = cTrans[i];
for (int j = 0; j < Con.Length - 1; j++)
{
now[i] += omega * Con[j] * history[j];
}
now[i] += omega * Con[Con.Length - 1];
if (Double.IsNaN(now[i]) || Double.IsInfinity(now[i]))
throw new Exception("错误:方程解出现NaN或者无穷大,请验证方程组的收敛性!");
}
times++;
//解是否符合条件
isTrueSolution = true;
for (int i = 0; i < now.Length; i++)
{
if (Math.Abs(now[i] - history[i]) > Epsilon)
{
isTrueSolution = false;
break;
}
}
//更新旧解
now.CopyTo(history, 0);
}
//超出迭代次数求解失败
t = times;
now.CopyTo(solution, 0);
if (times > IterativeTimes) return 1;
else
return 0;}
/// <summary>
/// Gauss-Seidel迭代法求解线性方程组
/// </summary>
/// <param name="c">方程组系数的增广矩阵</param>
/// <param name="IterativeTimes">最大迭代次数</param>
/// <param name="Epsilon">收敛标准</param>
/// <param name="t">迭代次数</param>
/// <param name="solution">求解结果</param>
/// <returns>执行结果,0表示求解成功</returns>
public static int Gauss_Seidel(List<double[]> c, int IterativeTimes, double Epsilon, out int t, double[] solution)
{
return SOR(c, IterativeTimes, Epsilon, 1, out t, solution);
}