Here I've implemented a 3D multi-link, rigid-body pendulum simulation from the Newton-Euler equations of motion, using explicit Euler integration, rotational damping, and Baumgarte stabilization of the hinge constraints. 1-8 links are combined into a single matrix representing the linear system of motion and constraints, which is solved using Numpy's linalg.solve function. The link's 3D rotations are stored and manipulated using quaternions.
An optional ground collision plane is placed at y=0 - press 'p' to toggle this on and off. Pendulums with < 3 links are too short to hit this! (Add links by pressing '+')
Requires:
- Python (I use 3.5)
- Numpy
- Pyquaternion
- PyOpenGL
- PyOpenGL-accelerate
- Matplotlib
Run:
python sim.py [-t|--track]
Options:
- -t/--track: Enable energy tracking
Controls:
- 'r' : reset the simulation
- 'SPACE' : toggle pause
- 'p' : toggle ground plane
- '+' : add a link - up to 8
- '-' : remove a link - minimum 1
- 's' : plot energy over time (requires tracking)
- 'q/ESC' : quit
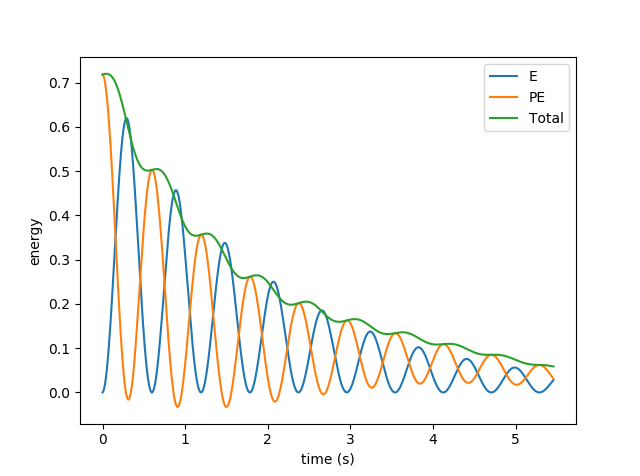
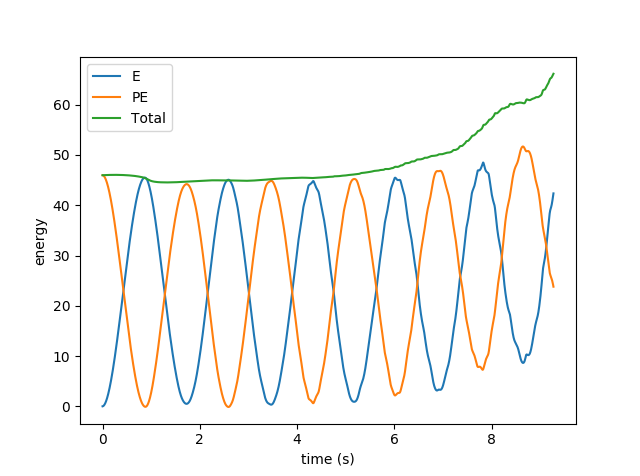
Pressing the 's' key during a tracked (--track command line option) simulation pops up a plot for the simulation's energy over time. This isn't interactive right now, but it gives an idea of how accurate the simulation is (not very!), and shows how kinetic and potential energy are traded off against one another.
Energy plot for fairly highly damped single-link pendulum:
Energy plot for 5-link pendulum colliding with ground plane, which was then removed:
Energy plot showing underdamped 8-link pendulum's energy accumulation (physically inaccurate):