pLam (pure Lambda calculus) is a tool to explore, define and evaluate various λ-expressions. Code written in pLam can be executed interactively within pLam's shell or stored in a file with .plam extension and run anytime.
Inside import/ directory, many useful λ-expressions are already implemented to be used as libraries.
pLam's AUR package is at https://aur.archlinux.org/packages/plam thanks to @Xmgplays.
Git Clone URL: https://aur.archlinux.org/plam.git
(coming soon...)
This project builds using Haskell tool stack documented at https://docs.haskellstack.org/en/stable/README/.
On most Unix systems, you can get stack by typing:
curl -sSL https://get.haskellstack.org/ | sh
or:
wget -qO- https://get.haskellstack.org/ | sh
On Windows, you can download 64-bit installer given at https://docs.haskellstack.org/en/stable/README/.
- clone project repository
git clone https://github.com/sandrolovnicki/pLam.git
- go to project directory
cd pLam
- setup stack on isolated location
stack setup
- use stack to build project
stack build
note: if build was not successful, it may be due to:
- curses library
- the solution is to install it (on Ubuntu:
sudo apt-get install libncurses5-dev libncursesw5-dev)
- the solution is to install it (on Ubuntu:
5.a) use stack to run project executable from project's directory
stack exec plam
5.b) use make_global.sh script to create a global command 'plam' that can be used to start pLam from anywhere in your system. The script will also change your import path in src/Config.hs so you need to build the project again.
sudo ./make_global.sh
stack build
Now, (and anytime in the future!), you can start pLam from anywhere in your system by just typing
plam
λ-variable is required to be lowercase and a single letter. For example, x is a good λ-variable for pLam and X, var,... are not. There are also environment variables (names for defined λ-expressions) which are every string that is not parsed as λ-variable, λ-abstraction or λ-application.
λ-abstraction is written the same as in the language of pure (untyped) λ-calculus, except that pLam treats a symbol \ as λ and it is required to write a space after .. For example, λx.λy.x would be written \x. \y. x in pLam. One can also write λ-abstraction in the "uncurried" form: \xy. x or \x y. x.
λ-application is written like 2 λ-expressions separated by a space, for example (\x. x) (\xy.x) or (\x. x) MyExpression or myexp1 myexp2. Brackets ( and ) are used as usual and are not required to be written for application association; the default association is to the left, so M N P is parsed as (M N) P and one only needs to specify with brackets if the intended expression should be M (N P).
A block of code in pLam is a line, and possible lines (commands) are the following:
- syntax:
<string> = <λ-expression> - semantics: let the
<string>be a name for<λ-expression>. - examples:
T = \x y. x,myexpression = T (T (\x. x) T) T - restriction:
<string>needs to be of length>1 or starting with uppercase letter
- syntax:
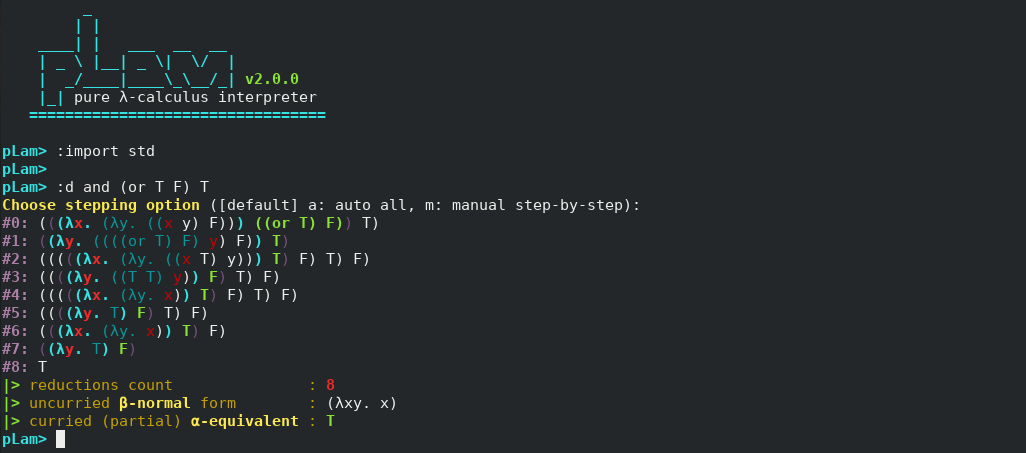
?<evop> ?<evop> <λ-expression>where<evop>s are evaluation options;:dand/or:cbv - semantics: reduce the
<λ-expression>to β-normal form. If:dis chosen as option, all the reduction steps will be shown. If:cbvis chosen as option, reductions will be performed in a call-by-value manner, first reducing the argument before substituting it for bound variable. That is, call-by-name is the default reduction option if:cbvis not chosen. - example:
\x y. x,:d T (T (\x. x) T) T,:d :cbv T (T (\x. x) T) T,:cbv and (or T F) T - example 2:
F omega Twill reduce toT, but:cbv F omega Twill run forever - restriction: none
- syntax:
:import <string> - semantics: put all the expressions defined in the file
import/<string>.plaminto the list of environment variables. - example:
:import std - restriction:
<string>.plamhas to be insideimport/directory within the pLam project directory
- syntax
:export <string> - semantics: put all the expressions in the list of environment variables into the file
import/<string>.plam - example:
:export test - restriction:
<string>.plamcannot already exist
- syntax:
--<string> - semantics: a comment line
- example:
-- this is a comment - restriction: none
- syntax:
:run <string> - semantics: runs a
.plamfile with relative path<string>.plam - example:
:run <relative-path-to-plam>/examples/2.5.2 - restrictions:
~for home does not work
- syntax:
:print <string> - semantics: prints
<string>to a new line. It mostly makes sense to use it in .plam programs to be executed, not in interactive mode where a comment should do the job better. - example:
:print this is a message - restrictions: none
pLam is equipped with some (optional) shortcuts to work with often used expressions.
Church numerals can be typed as 0, 1, 2,... and pLam parses those integers as λfx. x, λfx. f x, λfx. f (f x), ...
Similar to handling Church numerals, pLam also handles binary numerals from binary.plam library. You can type them as 0b, 1b, 2b, ... which is them parsed as λp. p (λxy. y) (λexy.x), λp. p (λxy. x) (λexy.x), λp. p (λxy. y) (λp. p (λxy. x) (λexy.x)), ...
Note that binary numerals are nothing standard, but something I implemented, so I suppose the only documentation for them is here.
List encoding is pretty standard; empty = T, append = λhtfl. l h t, and you can use syntact sugar which parses [1,2] into λfl. l 1 (λfl. l 2 empty), [T,\x.x] into λfl. l T (λfl. l (λx.x) empty) and so on...
NOTE: Output might be slightly different due to constant fixes and changes. Fully updated examples will be put each time they diverge too far from current.
All the examples can be found in examples/ directory.
pLam> :import booleans
pLam>
pLam> and (or F (not F)) (xor T F)
|> reductions count : 18
|> uncurried β-normal form : (λxy. x)
|> curried (partial) α-equivalent : T
pLam> :import std
pLam>
pLam> mul (add 2 (S 2)) (sub (exp 2 3) (P 8))
|> reductions count : 762
|> uncurried β-normal form : (λfx. f (f (f (f (f x)))))
|> curried (partial) α-equivalent : 5
pLam> :import std
pLam>
pLam> fFact = \f. \x. (isZ x) 1 (mul x (f (P x)))
pLam> Fact = Y fFact
pLam>
pLam> Fact 3
|> reductions count : 646
|> uncurried β-normal form : (λfx. f (f (f (f (f (f x))))))
|> curried (partial) α-equivalent : 6
pLam> :import std
pLam> :import comp
pLam>
pLam> fact = PR0 1 (C22 mul (C2 S I12) I22)
pLam> fact 3
|> reductions count : 898
|> uncurried β-normal form : (λfx. f (f (f (f (f (f x))))))
|> curried (partial) α-equivalent : 6
pLam> :import binary
pLam>
pLam> 0b
|> reductions count : 2
|> uncurried β-normal form : (λp.((p (λxy. y)) (λexy.x)))
|> curried (partial) α-equivalent : 0b
pLam>
pLam> 2048b
|> reductions count : 24
|> uncurried β-normal form : (λp.((p (λxy. y)) (λp.((p (λxy. y)) (λp.((p (λxy. y)) (λp.((p (λxy. y)) (λp.((p (λxy. y)) (λp.((p (λxy. y)) (λp.((p (λxy. y)) (λp.((p (λxy. y)) (λp.((p (λxy. y)) (λp.((p (λxy. y)) (λp.((p (λxy. y)) (λp.((p (λxy. x)) (λexy.x)))))))))))))))))))))))))
|> curried (partial) α-equivalent : (λp. ((p F) 1024b))
pLam>
pLam> addB 7b (subBs 2b 3b)
|> reductions count : 9458
|> uncurried β-normal form : (λp.((p (λxy. x)) (λp.((p (λxy. x)) (λp.((p (λxy. x)) (λexy.x)))))))
|> curried (partial) α-equivalent : 7b
pLam> :import list
pLam>
pLam> list = Merge [3,1] [2]
pLam> rlist = Reverse list
pLam>
pLam> Get 0 rlist
|> reductions count : 243
|> uncurried β-normal form : (λfx. f (f x))
|> curried (partial) α-equivalent : 2
pLam> Get 0 list
|> reductions count : 50
|> uncurried β-normal form : (λfx. f (f (f x)))
|> curried (partial) α-equivalent : 3
pLam>
pLam> QSort list
|> reductions count : 459
|> uncurried β-normal form : (λfl. (l (λfx. f x)) (λfl. (l (λfx. f (f x))) (λfl. (l (λfx. f (f (f x)))) (λfl. f))))
|> curried (partial) α-equivalent : (λf. (λl. ((l 1) (λf. (λl. ((l 2) (λf. (λl. ((l 3) empty)))))))))
pLam> :run examples/2.5.2
=================================
< zero
=================================
|> reductions count : 114
|> uncurried β-normal form : (λfx. f (f x))
|> curried (partial) α-equivalent : 2
plam ~/Projects/pLam/examples/2.5.2.plam
=================================
< zero
=================================
|> reductions count : 114
|> uncurried β-normal form : (λfx. f (f x))
|> curried (partial) α-equivalent : 2
Done.
I am not a Haskell expert. In fact, this is my first and only Haskell project. It is inevitable that existing code could be written better and I wish to do it in the upcoming future.
The goal of the project was to create an environment for easy building of new expressions from previously defined ones, so that one could explore λ-calculus. It was a helper tool so I could define and test a new numeral system in λ-calculus, for my master thesis. Now, when this all went well, the time is coming for me to get back to Haskell code.
If you would like to see some improvements or new features, you can open an issue. I will sort issues into milestones and you will know pretty quickly when to expect it to be done. If you can implement your ideas yourself, great! Pull requests are welcome.



