How to compute the Student's t-Distribution.
t分布の確率密度関数は ベータ関数(Beta function) を用いて以下のように定義される。
ベータ関数は ガンマ関数(Beta function) を用いて以下のように定義される。
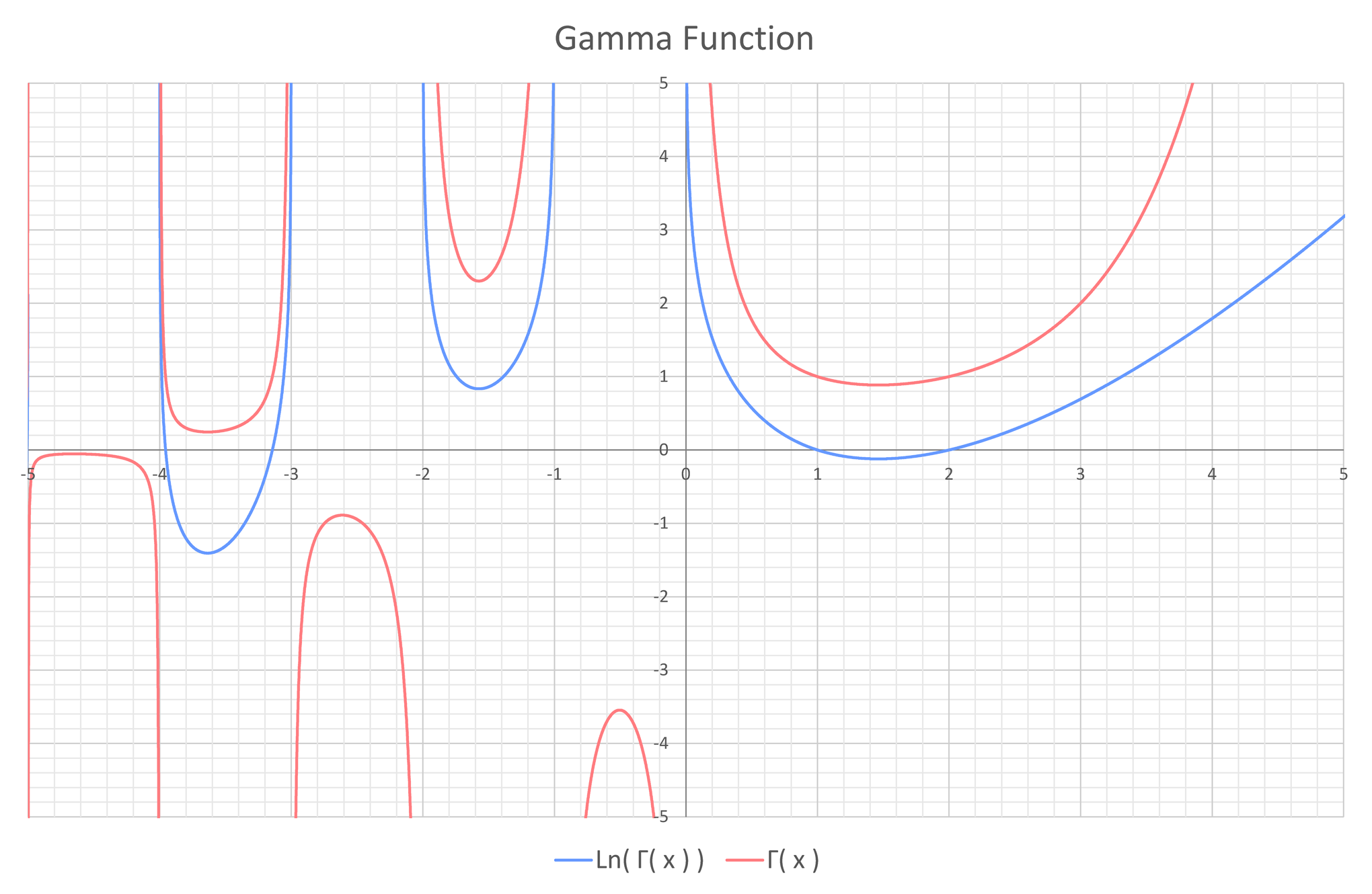
ガンマ関数の計算方法は以下を参照のこと。
* GammaFunc: How to compute the Gamma function.:LUXOPHIA:GitHub
t分布の累積分布関数は、下側確率(Lower tailed probability) とも呼ばれ、正則不完全ベータ関数(Regularized incomplete beta function) を用いて以下のように定義される。
正則不完全ベータ関数は 不完全ベータ関数(Incomplete beta function) と標準のガンマ関数を用いて以下のように定義される。
不完全ベータ関数は ガウスの超幾何関数(Gaussian hypergeometric function) を用いて以下のように定義される。しかしこのままでは、桁落ちが著しく数値計算に向かない。
そこで実装上は、以下の オイラーの変換公式(Euler's transformation) を用いて、
数値的安定性を高めた以下の定義式を用いる。
なお、超幾何関数は以下の 超幾何級数 によって計算することができ、
具体的な実装は以下のようになる。
function HypGeo21( const A_,B_,C_,X_:Double ) :Double;
var
P0, P1 :Double;
N :Integer;
begin
P0 := 1;
Result := P0;
for N := 0 to 10000 do
begin
P1 := ( ( A_ + N ) * ( B_ + N ) )
/ ( ( C_ + N ) * ( 1 + N ) ) * X_ * P0;
Result := Result + P1;
if Abs( P1 ) < DOUBLE_EPS3 then Break;
P0 := P1;
end;
end;不完全ベータ関数は、以下の 連分数(Continued fraction) によって定義される。
一般的な連分数の評価法 (L.Lorentzen and H.Waadeland, "Continued Fractions with Applications," North-Holland, Amsterdam, 1992.) を素直に実装すると以下のようになり、
function IncBeta( const X_,A_,B_:Double ) :Double;
var
G0, G2, C0, C1, P0, P1, P2, Q0, Q1, Q2, N2A :Double;
N, N2 :Integer;
begin
G2 := 0;
C1 := -X_ * ( A_ + B_ ) / ( A_ + 1 );
P0 := 0; P1 := 1; P2 := P1 + C1 * P0;
Q0 := 1; Q1 := 1; Q2 := Q1 + C1 * Q0;
for N := 1 to 10000 do
begin
G0 := G2; G2 := P2 / Q2;
if ( Abs( G2 - G0 ) < DOUBLE_EPS3 ) then Break;
N2 := N shl 1; N2A := N2 + A_;
C0 := +X_ * N * ( B_ - N ) / ( N2A * ( N2A - 1 ) );
C1 := -X_ * ( A_ + N ) * ( A_ + B_ + N ) / ( N2A * ( N2A + 1 ) );
P0 := P1; P1 := P2; P2 := P1 + C0 * P0;
Q0 := Q1; Q1 := Q2; Q2 := Q1 + C0 * Q0;
P0 := P1; P1 := P2; P2 := P1 + C1 * P0;
Q0 := Q1; Q1 := Q2; Q2 := Q1 + C1 * Q0;
end;
Result := Power( X_, A_ ) * Power( 1 - X_, B_ ) * G2 / A_;
end;より桁あふれを起こしにくい、Lentz's method (Lentz, W.J. 1976, Applied Optics, vol. 15, pp. 668–671.) を取り入れると、以下のような実装となる。
function IncBeta( const X_,A_,B_:Double ) :Double;
var
C0, C1, U0, U1, U2, V0, V1, V2, G0, G1, G2, N2A :Double;
N, N2 :Integer;
begin
C1 := -X_ * ( A_ + B_ ) / ( A_ + 1 );
U1 := 2; U2 := 1 + C1 / U1;
V1 := 1; V2 := 1 + C1 / V1;
G0 := 1; G1 := U1 / V1 * G0; G2 := U2 / V2 * G1;
for N := 1 to 10000 do
begin
if ( Abs( G2 - G0 ) < DOUBLE_EPS3 ) then Break;
N2 := N shl 1; N2A := N2 + A_;
C0 := +X_ * N * ( B_ - N ) / ( N2A * ( N2A - 1 ) );
C1 := -X_ * ( A_ + N ) * ( A_ + B_ + N ) / ( N2A * ( N2A + 1 ) );
U0 := U2; U1 := 1 + C0 / U0; U2 := 1 + C1 / U1;
V0 := V2; V1 := 1 + C0 / V0; V2 := 1 + C1 / V1;
G0 := G2; G1 := U1 / V1 * G0; G2 := U2 / V2 * G1;
end;
Result := Power( X_, A_ ) * Power( 1 - X_, B_ ) * ( G2 - 1 ) / A_;
end;定義式(3)は、下側確率を直接計算できるものの、下図のように絶対値の大きい定義域で計算が不安定となる。
by Hypergeometric series by Continued fraction
この現象は、式(3)において 自由度(Degree of freedom)νが大きい場合、つまり式(4)において引数a,bが両方とも大きい場合に、不完全ベータ関数の計算が不安定になることが原因である。
そこで、正則不完全ベータ関数の引数の片方を1/2に固定することができる 両側確率(Two tailed probability) の定義式を利用する。
下側確率CumDistTは、以下のように両側確率Cum2DistTを繋ぎ合わせることで再定義可能である。
function CumDistT( const X_,V_:Double ) :Double;
begin
Result := Cum2DistT( X_, V_ ) / 2;
if 0 < X_ then Result := 1 - Result;
end;すると、不完全ベータ関数の計算が安定するので、絶対値の大きい定義域においても非常に安定する。 しかし今度は逆に、絶対値の小さい定義域において精度が大幅に低下してしまった。
そこで正則不完全ベータ関数の関係式を用いて、
以下のように引数の順序を交換した定義式を併用する。
すると今度は、絶対値の小さい定義域で安定し、絶対値の大きい定義域で発散するようになる。定義式(3)と似た特性ではあるが、格段に安定している。
つまり、原点付近では式(13)を、それ以外では式(10)を、と適宜切り替えることで、xの全域を高精度にサポートすることができる。
我々の実装では経験的に導いた Abs(x) < Sqrt(ν)/10 という切り替え条件を採用している。
function Cum2DistT( const X_,V_:Double ) :Double;
var
X2 :Double;
begin
X2 := Pow2( X_ );
if 100 * X2 < V_ then Result := 1 - RegIncBeta( X2 / ( X2 + V_ ), 1 / 2, V_ / 2 )
else Result := RegIncBeta( V_ / ( X2 + V_ ), V_ / 2, 1 / 2 );
end;3. 逆累積分布関数(Quantile function)
逆累積分布関数は累積分布関数の 逆関数(Inverse function) であり、与えられた下側確率に対応するxの値、つまり パーセント点(Percentage point) を逆算する関数である。近似式を使った解法が一般的ではあるが、我々の実装では ニュートン法(Newton's method) を用いて厳密に解を求めている。
分布関数を積分したものが累積分布関数なので、累積t分布関数CumDistTの微分値はt分布関数DistTそのものとなる。我々は以下のように、関数値と微分値を同時に出力する関数を実装した。
function CumDistT( const X_:TdDouble; const V_:Double ) :TdDouble;
begin
with X_ do
begin
Result.o := CumDistT( o, V_ ) ;
Result.d := DistT( o, V_ ) * d;
end;
end;その上で、ニュートン法を実行し逆関数値を検索するInvCumDistT関数を実装した。
function InvCumDistT( const P_,V_:Double ) :Double;
var
X, P :TdDouble;
Pd :Double;
begin
X := TdDouble.Create( 0, 1 );
repeat
P := CumDistT( X, V_ );
Pd := P.o - P_;
X.o := X.o - Pd / P.d;
until Abs( Pd ) < DOUBLE_EPS3;
Result := X.o;
end;