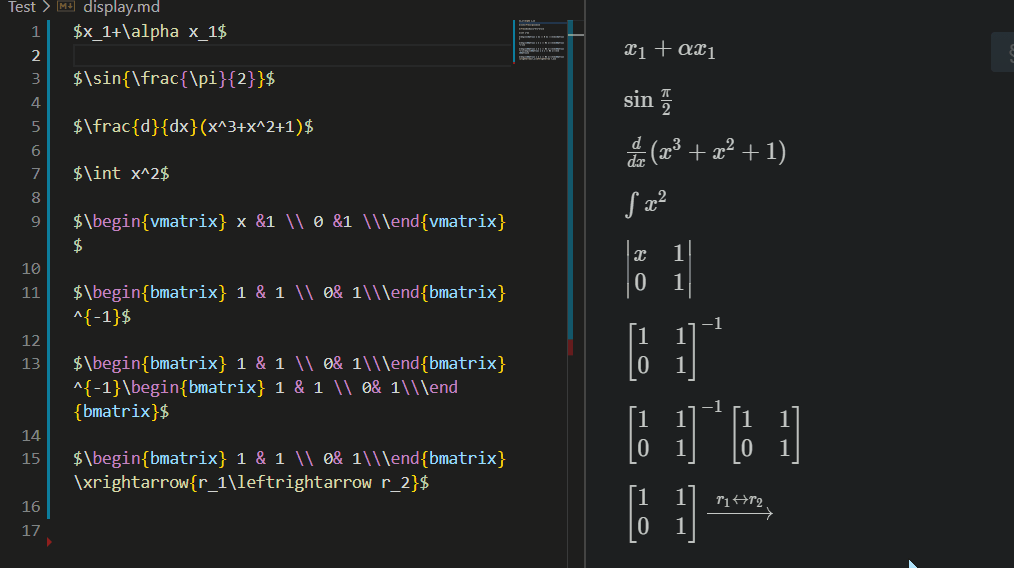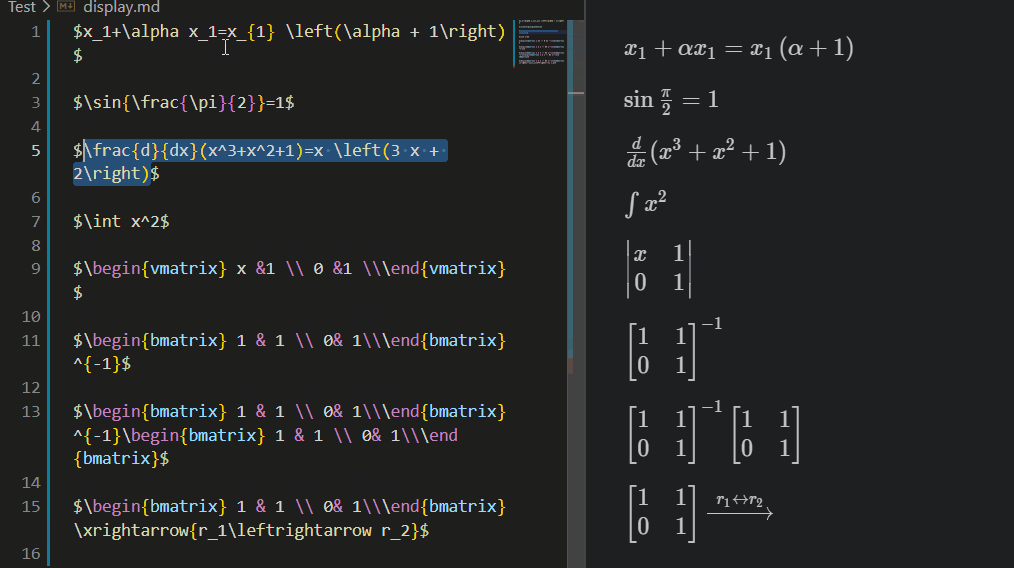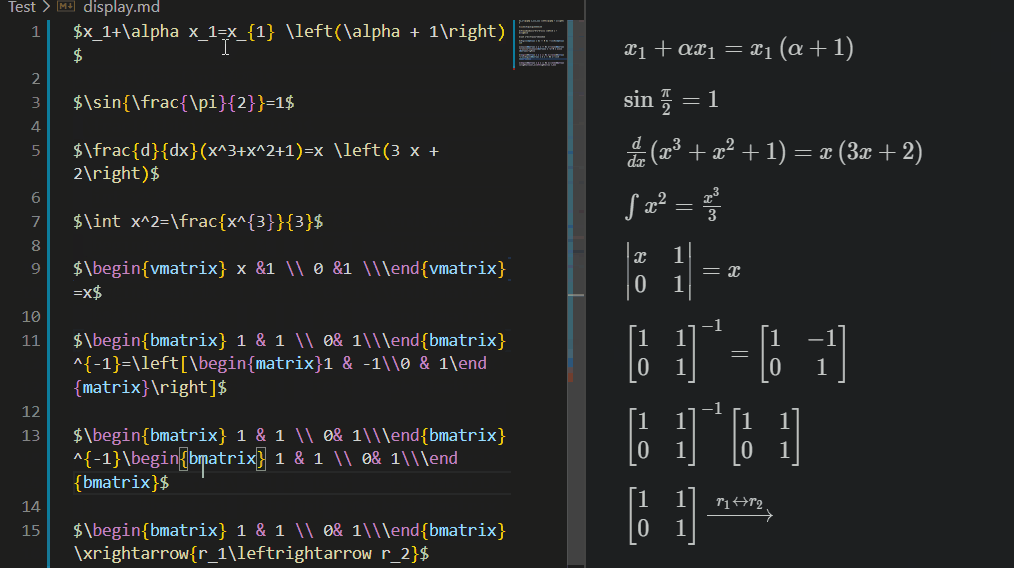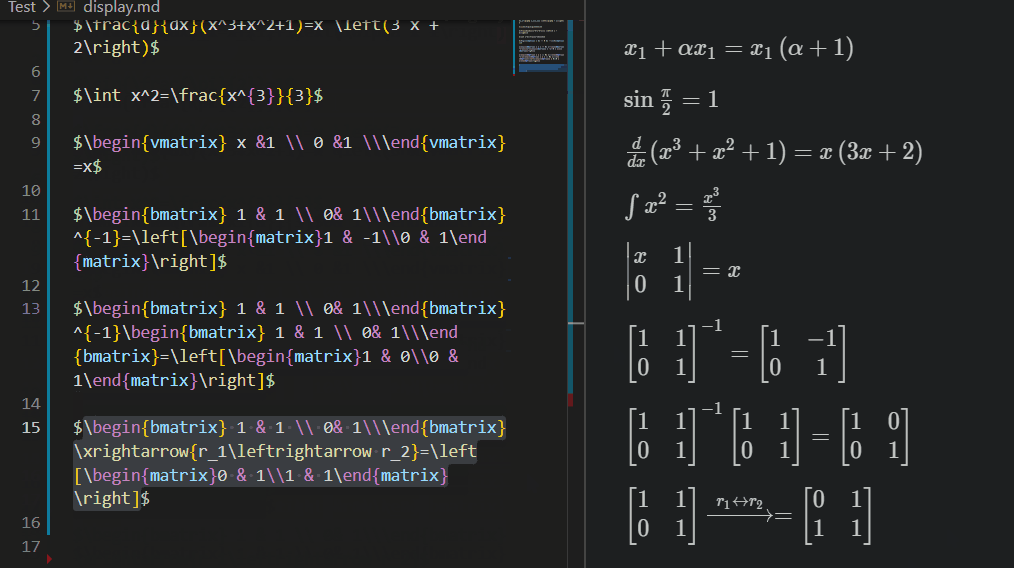
Latex Sympy Calculator

About

Latex Sympy Calculator parses LaTeX math expressions and converts it into the equivalent SymPy form. Then, calculate it and convert to latex result.

It is designed for providing people writing in latex or markdown a ability to calculate something when writing math expression. It is based on Python, Sympy and latex2sympy2 module.

PS: If you want to install the extension, PLEASE READ THE INSTALL DESCRIPTION!

Features

• Arithmetic: Add (+), Sub (-), Dot Mul (·), Cross Mul (×), Frac (/), Power (^), Abs (|x|), Sqrt (√), etc...
• Alphabet: a - z, A - Z, α - ω, Subscript (x_1), Accent Bar(ā), etc...
• Common Functions: gcd, lcm, floor, ceil, max, min, log, ln, exp, sin, cos, tan, csc, sec, cot, arcsin, sinh, arsinh, etc...
• Funcion Symbol: f(x), f(x-1,), g(x,y), etc...
• Calculous: Limit ($lim_{n\to\infty}$), Derivation ($\frac{d}{dx}(x^2+x)$), Integration ($\int xdx$), etc...
• Linear Algebra: Matrix to raw echelon form, Determinant, Transpose, Inverse, Elementary Transformation, etc...
• Other: Binomial...

Install

IT IS IMPORTANT!
IT IS IMPORTANT!
IT IS IMPORTANT!

Before you use the extension, please install python and two python modules: latex2sympy and Flask.

Install Python in Python.org, and then install NECESSARY modules by running:

pip install latex2sympy2
pip install Flask

If you have installed it, you can run the code in terminal to test if you have installed it successfully.

python

# Get into python environment
import latex2sympy2
import flask

If you want to use this extension in Remote - SSH or Remote - WSL, please uninstall the original extension and reinstall it in the remote server.

Usage

Latex to Latex

You can SELECT some text, and press Shift + Ctrl + Alt + E (equal) to get the result of the selected Latex text. It will be like:

# Before
\frac{d}{dx}(x^3+x^2+1)

# After
\frac{d}{dx}(x^3+x^2+1) = x (3 x + 2) 

You can SELECT some text, and press Shift + Ctrl + Alt + R (replace) to get the result of the selected Latex text. It will be like:

# Before
\frac{d}{dx}(x^3+x^2+1)

# After
x (3 x + 2) 

Factor and Expand

You can SELECT some text, and press Shift + Ctrl + Alt + F (factor) to get the factor of the selected Latex text. It will be like:

# Before
x^{2} + 2 x y + y^{2}

# After
(x + y)^{2}

If you are using windows, the shortcut Shift + Ctrl + Alt + F may be invalid, you can set another shortcut for it.

You can SELECT some text, and press Shift + Ctrl + Alt + X (expand) to get the expand of the selected Latex text. It will be like:

# Before
(x + y)^{2}

# After
x^{2} + 2 x y + y^{2}

Latex to Numerical Result

You can SELECT some text, and press Shift + Ctrl + Alt + N (numerical) to get the numerical result of the selected Latex text. It will be like:

# Before
\sqrt{2}

# After
1.41421356237310

Solve Equation

# Before
x + y = 1

# After
[ y = 1 - x, \  x = 1 - y]

Eval At

# Before
(x+2)|_{x=y+1}

# After
y + 3

Matrix to raw echelon form

You can SELECT matrix, then press Shift + Ctrl + Alt + T to transform it to raw echelon form in one action

# Before
\begin{bmatrix}
    1 & 2 & 3\\
    4 & 5 & 6\\
    7 & 8 & 9
\end{bmatrix}

# After 
\begin{bmatrix}
    1 & 2 & 3\\
    4 & 5 & 6\\
    7 & 8 & 9
\end{bmatrix} \to \begin{bmatrix}1 & 0 & -1\\0 & 1 & 2\\0 & 0 & 0\end{bmatrix}

Variances

You can ASSIGN variance a value. Use Shift + Ctrl + Alt + D (define) and grammar like y = x + 1.

# Shift + Ctrl + D
y = x + 1

# Shift + Ctrl + E
# Before
2y
# After
2y = 2 x + 2

PS: You can use grammar like y == x + 1 to describe the relation of equality.

If you want to see the bonding of variances, you can press Shift + Ctrl + P, and input latex-sympy-calculator: Show Current variances, then you will get data like:

y = x + 1
z = 2x

If you want to remove the bonding of variances, you can press Shift + Ctrl + P, and input latex-sympy-calculator: Reset Current variances, then you can clear the current variances.

If you want to let your variances be complex numbers, you can press Shift + Ctrl + P, and input latex-sympy-calculator: Toggle Complex Number Support For Variances.

For example, x = 1 + 2i, \int \cos xe^{-ikx}dx.

Matrix Symbol

You can DEFINE variance a matrix symbol. Use Shift + Ctrl + Alt + D (define) and grammar like X \in \mathbb{R}^{n \times m}.

# Shift + Ctrl + D
X \in \mathbb{R}^{n \times m}

# Shift + Ctrl + E
# Before
X X^{T} X
# After
X X^{T} X

# Shift + Ctrl + E
# Before
X^{-1} X
# After
I

Python

You can calculate a python expression by Shift + Ctrl + Alt + P.

You can use all sympy expression in it.

For example, you can get variances you assigned by:

# Before
var['y']

# After
var['y'] = x + 1

Calculator the roots of the equation:

# Before
solve([2 * x - y - 3, 3 * x + y - 7],[x, y])

# After
solve([2 * x - y - 3, 3 * x + y - 7],[x, y]) = {x: 2, y: 1}

Convert latex to sympy and convert sympy to latex:

# Latex to Sympy
expr = latex2sympy(r'x^2 + 3x + 1')

# Sympy to Latex
latex = latex(expr)

# Latex to Latex
result = latex2latex(r'\frac{d}{dx}(x^3+x^2+1)')

For example, you can calculator eigenvector with problem solving process:

For matrix: $A=\begin{bmatrix}	5 &6 &-3 \\	-1 &0 &1 \\	1 &2 &-1 \\\end{bmatrix}$

Let $B=\lambda\begin{bmatrix}1 &0 &0 \\0 &1 &0 \\0 &0 &1 \\\end{bmatrix}-\begin{bmatrix}	5 &6 &-3 \\	-1 &0 &1 \\	1 &2 &-1 \\\end{bmatrix}=\left[\begin{matrix}\lambda - 5 & -6 & 3\\1 & \lambda & -1\\-1 & -2 & \lambda + 1\end{matrix}\right]$

Its determinant is $latex(var["B"].doit().det()) = \lambda^{3} - 4 \lambda^{2} + 2 \lambda + 4$

Factor it: $latex(factor(var["B"].doit().det())) = \left(\lambda - 2\right) \left(\lambda^{2} - 2 \lambda - 2\right)$

Solve for eigenvalues $latex(solve(var["B"].doit().det())) = \left[ 2, \  1 - \sqrt{3}, \  1 + \sqrt{3}\right]$

Or via:$latex(var["A"].eigenvals()) = \left\{ 2 : 1, \  1 - \sqrt{3} : 1, \  1 + \sqrt{3} : 1\right\}$

Let $\lambda_1=2, \lambda_2=1-\sqrt{3}, \lambda_3=1+\sqrt{3}$

So $B_1=\lambda_1\begin{bmatrix}1 &0 &0 \\0 &1 &0 \\0 &0 &1 \\\end{bmatrix}-\begin{bmatrix}	5 &6 &-3 \\	-1 &0 &1 \\	1 &2 &-1 \\\end{bmatrix}=\left[\begin{matrix}-3 & -6 & 3\\1 & 2 & -1\\-1 & -2 & 3\end{matrix}\right]$

Assign it: $B_1=\left[\begin{matrix}-3 & -6 & 3\\1 & 2 & -1\\-1 & -2 & 3\end{matrix}\right]$

Simplify it by elementary row transformations:

$latex(var["B_1"].doit().rref()) = \left( \left[\begin{matrix}1 & 2 & 0\\0 & 0 & 1\\0 & 0 & 0\end{matrix}\right], \  \left( 0, \  2\right)\right)$

For the eigenvalue $\lambda_1=2$, its one eigenvector is $\xi_1=\begin{pmatrix}-2\\1\\0\end{pmatrix}$

So for the eigenvalue $\lambda_1=2$ its all eigenvectors are $k_1\xi_1 \ (k_1\neq 0, k_1\in P)$

In a same way, all eigenvalues and eigenvector are

$latex(var["A"].eigenvects()) = \left[ \left( 2, \  1, \  \left[ \left[\begin{matrix}-2\\1\\0\end{matrix}\right]\right]\right), \  \left( 1 - \sqrt{3}, \  1, \  \left[ \left[\begin{matrix}6 - 3 \sqrt{3}\\-2 + \sqrt{3}\\1\end{matrix}\right]\right]\right), \  \left( 1 + \sqrt{3}, \  1, \  \left[ \left[\begin{matrix}3 \sqrt{3} + 6\\-2 - \sqrt{3}\\1\end{matrix}\right]\right]\right)\right]$

License

This project is licensed under the MIT License.