up

material/aulas/IA/lab07/index.md

@@ -0,0 +1,293 @@
+
+# Deep Learning e Visão Computacional usando TensorFlow
+
+Este tutorial é um guia rápido de consulta para o mundo do deep learning. 
+
+Aqui você encontra por meio de exemplos um pouco de teoria para compreesão e aplicação dos conceitos.
+
+## Objetivos
+
+1. [Introdução](#introdução)
+2. [Configuração e Instalação](#configuração-e-instalação)
+3. [Entendendo os Conceitos Básicos](#entendendo-os-conceitos-básicos)
+   - [Perceptron](#perceptron)
+   - [Perceptron de Múltiplas Camadas (MLP)](#perceptron-de-múltiplas-camadas-mlp)
+   - [Retropropagação](#retropropagação)
+   - [Otimizadores](#otimizadores)
+4. [Redes Neurais Convolucionais (CNN)](#redes-neurais-convolucionais-cnn)
+5. [Implementando uma MLP Simples](#implementando-uma-cnn-simples)
+6. [Treinando o Modelo](#treinando-o-modelo)
+7. [Avaliação e Conclusão](#avaliação-e-conclusão)
+
+# Introdução
+
+Deep learning é um subconjunto de aprendizado de máquina onde redes neurais artificiais, algoritmos inspirados no cérebro humano, aprendem a partir de grandes quantidades de dados. Da mesma forma, visão computacional é um campo da inteligência artificial que treina computadores para interpretar e compreender o mundo visual.
+
+## Configuração e Instalação
+
+Primeiro, certifique-se de que Python e TensorFlow estão instalados em seu sistema. Você pode instalar o TensorFlow com o seguinte comando:
+
+```bash
+pip install tensorflow
+```
+
+## Entendendo os Conceitos Básicos
+
+### Perceptron
+
+O **Perceptron** é um modelo de rede neural simples, geralmente utilizado para classificação binária. Consiste em uma única camada de neurônios, e sua operação pode ser descrita pela fórmula:
+
+![](percep.png)
+
+
+Podemos calcular o valor de um neuronio da seguinte forma:
+
+
+output = activation_function(weighted_sum + bias)
+
+ O perceptron é uma das formas mais simples de uma rede neural, utilizado para classificação binária. A saída de um neurônio no perceptron pode ser calculada usando a seguinte fórmula:
+
+```python
+output = activation_function(weighted_sum + bias)
+```
+
+Onde: 
+
+  - `weighted_sum`: é a soma ponderada das entradas (inputs) multiplicadas pelos respectivos pesos (weights).
+  - `activation_function`: refere-se à função que define o limiar de ativação do neurônio, como sigmoid, relu ou softmax.
+  - `bias`: é um termo adicional que permite ajustar a saída ao longo da função de ativação para melhor adaptação dos dados
+
+
+### Perceptron de Múltiplas Camadas (MLP)
+
+
+O `MLP (Multilayer Perceptron)` é uma extensão do modelo perceptron que inclui múltiplas camadas. A estrutura típica de um MLP consiste em:
+
+  - `Uma camada de entrada`, que recebe os dados.
+  - `Uma ou mais camadas ocultas`, que transformam os dados de entrada através de pesos, biases e funções de ativação.
+  - `Uma camada de saída`, que produz a previsão final do modelo.
+
+Cada camada é `totalmente conectada` à próxima, o que significa que cada neurônio em uma camada está conectado a todos os neurônios na camada seguinte. O MLP é capaz de aprender representações não-lineares dos dados, o que o torna adequado para problemas complexos de classificação e regressão.
+
+![](mlp.png)
+
+
+### Funções de Ativação
+
+As **funções de ativação** são componentes essenciais nas redes neurais, responsáveis por introduzir não-linearidades no modelo. Sem elas, a rede seria essencialmente um modelo linear e incapaz de aprender e representar dados complexos que requerem não-linearidade para sua modelagem. As funções de ativação decidem se um neurônio deve ser ativado ou não, com base no valor da soma ponderada de suas entradas.
+
+#### Exemplos Comuns:
+- **`ReLU (Rectified Linear Unit)`**: Oferece uma resposta linear para todos os valores positivos e zero para valores negativos. É a mais usada devido à sua eficiência computacional e à capacidade de mitigar o problema do desaparecimento do gradiente em redes profundas.
+- **`Sigmoid`**: Transforma os valores em uma faixa entre 0 e 1, útil especialmente para modelos onde precisamos de uma probabilidade como saída; contudo, é menos usada em camadas ocultas devido a problemas de desaparecimento de gradiente.
+- **`Tanh (Tangente Hiperbólica)`**: Semelhante à sigmoid, mas transforma os valores em uma faixa entre -1 e 1, centrando os dados e, portanto, melhorando a eficiência do aprendizado nas camadas ocultas.
+
+
+### Retropropagação (Backpropagation)
+
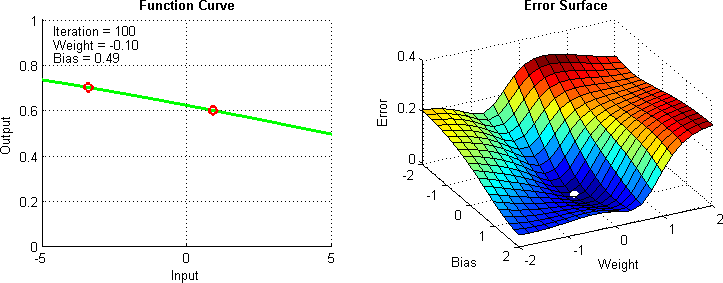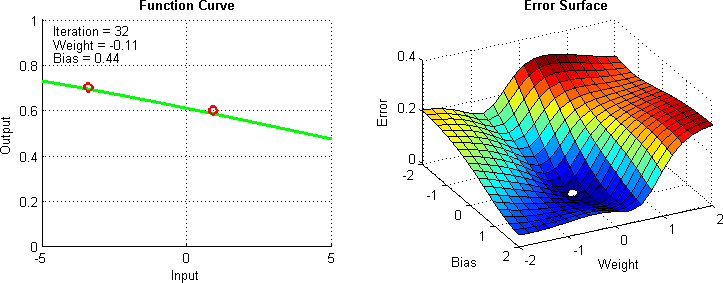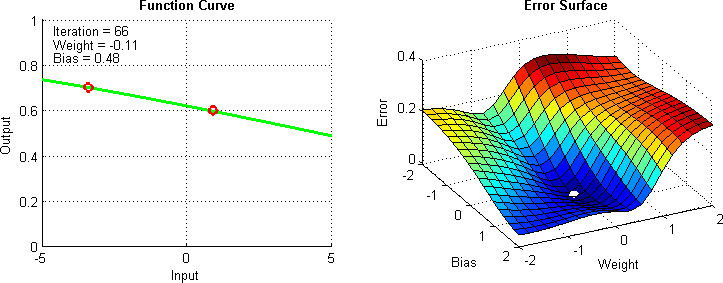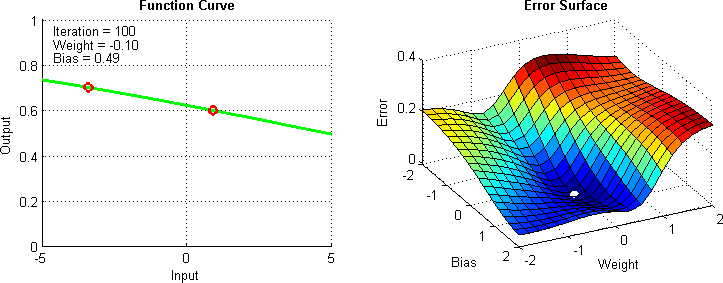
+A **Retropropagação** é uma técnica para treinar redes neurais, permitindo o ajuste dos pesos de conexão após cada iteração de treinamento. Este método utiliza o `cálculo do gradiente` da `função de perda` em relação a cada peso, propagando o erro de saída de volta pela rede para atualizar os pesos. Isso minimiza a função de perda ao longo do tempo, melhorando a precisão do modelo ao ajustá-lo mais eficazmente aos dados de treinamento.
+
+#### Funcionamento:
+
+- Calcula-se o gradiente da função de perda para determinar a direção na qual os pesos devem ser ajustados para minimizar o erro.
+- Os pesos são atualizados utilizando este gradiente, geralmente com a ajuda de um otimizador como SGD, Adam, entre outros.
+- Este processo é repetido para cada lote de dados (batch) durante várias épocas, ajustando progressivamente os pesos para melhorar o desempenho do modelo.
+
+Esses ajustes permitem que a rede aprenda de forma eficiente, refinando seus pesos para reduzir o erro total e aumentar a precisão nas tarefas de classificação ou regressão.
+
+### Otimizadores
+
+**Otimizadores** são algoritmos projetados para otimizar o processo de treinamento de uma rede neural, ajustando os pesos e a taxa de aprendizagem. É importante para determinar a rapidez e eficácia com que uma rede neural aprende. 
+
+Alguns exemplos comuns incluem:
+
+  - SGD (Descida do Gradiente Estocástico)
+  - Adam
+  - RMSprop
+  - Dentre outros, cada um com suas próprias características e adequações a diferentes tipos de problemas e conjuntos de dados.
+
+
+![grad](https://media.giphy.com/media/jUvoKxaLa7kxG/giphy.gif)
+
+### Redes Neurais Convolucionais (CNN)
+
+**Redes Neurais Convolucionais (CNNs)** são uma classe especializada de redes neurais profundas que são particularmente para tarefas de processamento de imagem e vídeo. Utilizam o processo de convolução para capturar características visuais importantes como bordas, texturas e padrões mais complexos sem a necessidade de intervenção ou extração manual de características.
+
+### Principais Componentes
+
+- **Camadas Convolucionais**: O coração de uma CNN. Estas camadas utilizam filtros que realizam a convolução sobre a entrada para criar mapas de características que resumem as presenças de características específicas na entrada.
+- **Função de Ativação**: Normalmente, uma função ReLU é aplicada após cada convolução para introduzir não-linearidades ao modelo, ajudando-o a aprender mais complexidades.
+- **Camadas de Pooling**: Seguem as camadas convolucionais e são usadas para reduzir as dimensões dos mapas de características, o que ajuda a diminuir o cálculo necessário e também controla o overfitting.
+- **Camadas Densas (Fully Connected Layers)**: Após várias camadas convolucionais e de pooling, a rede utiliza uma ou mais camadas densas onde a classificação final é realizada baseada nas características extraídas anteriormente.
+
+#### Funcionamento
+
+Uma CNN recebe uma imagem como entrada, que é passada através de uma série de camadas convolucionais com filtros (kernels), camadas de pooling, e eventualmente camadas densas para produzir uma saída, que pode ser uma classificação ou outra interpretação da imagem. Em cada camada convolucional, a rede aprende a identificar características cada vez mais complexas. À medida que os dados avançam pela rede, a "visão" da rede torna-se cada vez mais abstrata, permitindo que ela reconheça grandes padrões compostos por características menores capturadas nas primeiras camadas.
+
+#### Aplicações
+
+As CNNs têm sido usadas com grande sucesso em uma variedade de aplicações de visão computacional:
+
+- **`Reconhecimento de Imagens`**: Identificação de objetos, pessoas, cenas e atividades em imagens.
+- **`Classificação de Imagens`**: Classificar imagens em categorias pré-definidas.
+- **`Detecção de Objetos`**: Localizar e identificar múltiplos objetos dentro de uma única imagem.
+- **`Segmentação Semântica`**: Classificar cada pixel de uma imagem em uma categoria de objeto, permitindo uma compreensão detalhada da cena.
+
+
+## Implementando um MLP Simples
+
+Vamos implementar um exemplo simples de uma rede neural multicamadas (MLP) usando TensorFlow, aplicada ao conjunto de dados `MNIST`, que consiste em `imagens de dígitos escritos à mão`:
+
+![](mnist-samples.png)
+
+
+### Importando o dataset e bibliotecas
+
+Começamos importando a biblioteca `tensorflow` e o dataset mninst. Esse dataset é bem famoso e faz parte dos do da biblioteca tensorflow. Precisamos fazer uma transformação simples nas imagens de entrada para normalizar entre 0 e 1.
+
+```python
+import tensorflow as tf
+
+# Carregando o conjunto de dados MNIST
+mnist = tf.keras.datasets.mnist
+(x_train, y_train), (x_test, y_test) = mnist.load_data()
+
+# Normalizando os dados
+x_train, x_test = x_train / 255.0, x_test / 255.0
+```
+
+
+### Criando a Rede Neural
+
+Para construir nossa rede neural, utilizaremos a classe Sequential do TensorFlow, que permite compor modelos camada por camada de maneira simples e direta. Aqui está o detalhamento de cada componente utilizado:
+
+!!! warning
+    Substitua os campos `<QUANTIDADE_NEURONIOS> `e `<FUNCAO_ATIVACAO>` nos lugares indicados para configurar o número de neurônios e as funções de ativação.
+
+!!! tip
+    A quantidade de neurônios na `camada de saída` deve ser igual à quantidade de classes a serem preditas no MNIST, que são 10 (dígitos de 0 a 9).
+
+!!! tip
+    Utilize a função de ativação `relu` para as camadas intermediárias, pois ajuda a resolver o problema do desaparecimento do gradiente em redes profundas. Para a camada de saída, use `softmax` para converter as saídas em probabilidades de pertencimento às classes.
+
+
+#### Componentes do Modelo
+
+- `Sequential`: Esta é a classe base para definir uma pilha de camadas de rede neural. Você começa com uma lista vazia e adiciona camadas usando a notação de lista. Cada camada adicionada é empilhada sobre a anterior, o que facilita a modelagem de um fluxo de dados direto (feedforward).
+- `Flatten`: Transforma a matriz 2D de entrada (28x28 pixels da imagem) em um vetor 1D. Isso é necessário porque a primeira camada densa (Dense) espera um vetor como entrada.
+- `Dense`: É a camada de neurônios densamente conectados ou completamente conectados. Cada neurônio recebe entrada de todos os neurônios da camada anterior, mantendo uma conexão densa.
+  - <QUANTIDADE_NEURONIOS>: Aqui você define quantos neurônios deseja nesta camada.
+  - <FUNCAO_ATIVACAO>: Define a função de ativação a ser usada. A função relu é comum para camadas internas.
+
+
+
+```python
+# Criando o modelo MLP
+model = tf.keras.models.Sequential([
+  tf.keras.layers.Flatten(input_shape=(28, 28)),
+  tf.keras.layers.Dense(<QUANTIDADE_NEURONIOS>, activation=<FUNCAO_ATIVACAO>),
+  tf.keras.layers.Dense(<QUANTIDADE_NEURONIOS>, activation=<FUNCAO_ATIVACAO>)
+])
+```
+
+## Compilando o Modelo
+
+Agora, vamos compilar o modelo utilizando o `otimizador Adam` e a função de perda `sparse_categorical_crossentropy`, adequada para classificação de múltiplas classes onde as classes são fornecidas como números inteiros:
+
+
+!!! warning
+    Substitua os campos `<KEY>` por valores convenientes. Para `<METRICA>` utilize `accuracy`.
+
+
+```python
+model.compile(optimizer=<OTIMIZADOR>, 
+              loss=<LOSS>, 
+              metrics=[<METRICA>])
+```
+
+## Compilando o Modelo
+
+Agora, vamos compilar o modelo passando os conjuntos de dados `x_train` e `y_train`, definindo a quantidade épocas de treinamento e ajustando um subset de 20% para validação. 
+
+!!! warning
+    Substitua os campos `<KEY>` por valores convenientes. Defina 30 épocas e 0.2 de valiçao.
+
+```python
+# Treinando o modelo
+epocas_hist = model.fit(<X_TREINO>, <Y_TREINO>, epochs=<EPOCAS>, validation_split=<VALIDACAO>)
+```
+
+## Visualizando o historico de treinamento
+
+O historico de treinamento é salvo na variavel `epocas_hist`, podemos visualizar utlizando o pandas
+
+```python
+import pandas as pd
+
+df_historico = pd.DataFrame(epocas_hist.history)
+df_historico.info()
+
+df_historico[['loss','val_loss']].plot(); plt.show();
+df_historico[['accuracy','val_accuracy']].plot(); plt.show();
+
+```
+
+## Avaliação e Conclusão
+
+Após o treinamento, avaliamos o modelo no conjunto de teste para verificar sua acurácia e a perda:
+
+!!! warning
+    Substitua os campos `<KEY>` por valores convenientes. 
+
+
+
+```python
+test_loss, test_acc = model.evaluate(<X_TESTE>, <Y_TESTE>)
+print(f"Teste Acurácia: {test_acc:.3f}, Teste Loss: {test_loss:.3f}")
+
+```
+
+## Salvando o modelo
+
+```python
+# Salvando o modelo treinado
+model.save('mnist_mlp_model.h5')
+```
+
+## Importando uma Imagem e Usando com o Modelo Treinado
+
+Para usar uma imagem própria e verificar como o modelo MLP prevê o dígito, precisamos garantir que a imagem seja processada de maneira semelhante ao conjunto de dados MNIST. A imagem deve ser em escala de cinza, de tamanho 28x28 pixels, e normalizada.
+
+```python
+import tensorflow as tf
+from tensorflow.keras.preprocessing import image
+import numpy as np
+import matplotlib.pyplot as plt
+
+# Carregando o modelo treinado (certifique-se de que o modelo está disponível)
+model = tf.keras.models.load_model('mnist_mlp_model.h5')
+
+# Função para carregar e preparar a imagem
+def load_and_prepare_image(filepath):
+    img = image.load_img(filepath, color_mode='grayscale', target_size=(28, 28))
+    img = image.img_to_array(img)
+    img = img.reshape(1, 28, 28)
+    img = img.astype('float32')
+    img /= 255.0
+    return img
+
+# Caminho para a sua imagem
+filepath = 'path_to_your_image.png' # escolha uma imagem com um numero simples 
+
+# Carregando e preparando a imagem
+img = load_and_prepare_image(filepath)
+
+# Fazendo a previsão
+predictions = model.predict(img)
+predicted_digit = np.argmax(predictions)
+
+# Mostrando a imagem e a previsão
+plt.imshow(img.reshape(28, 28), cmap='gray')
+plt.title(f'Previsão: {predicted_digit}')
+plt.show()
+
+```

mkdocs.yml

@@ -124,6 +124,7 @@ nav:
       - Lab05 - Validação cruzada: aulas/IA/lab05/validacaocruzada.ipynb
       - Lab06 - Redes Neurais - Percepton : aulas/IA/lab06/rna.ipynb
       - Lab07 - Redes Neurais - MLP: aulas/IA/lab07/mlp.ipynb
+      - Lab07 - Redes Neurais - TensorFlow: aulas/IA/lab07/index.md
       - BATALHA DAS REDES: aulas/IA/batalharedes/batalha_das_redes.ipynb
       - Lab08 - Redes Neurais - CNN: aulas/IA/lab08/cnn.ipynb
       - Lab9 - Redes Neurais - Transfer learning: aulas/IA/lab09/transferlearning.ipynb