Samuel Bailey <sam@bailey.geek.nz>
An implementation of Tsai's camera calibration algorithm.
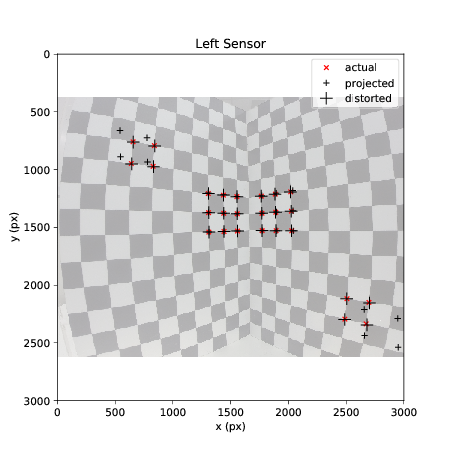
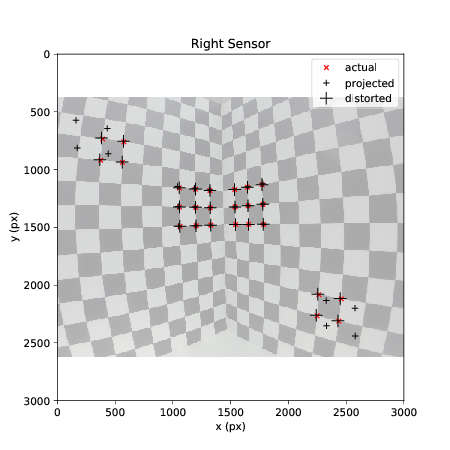
Camera calibration is the process of estimating the parameters of a mathematical model to approximate the properties of a physical camera. In this implementation a pinhole camera model with radial lens distortion is used. A combination of linear and non-linear optimisation methods (SVD and gradient descent) are used to find the parameters. Fast and accurate calibration can be achieved using only a single photograph of a suitable calibration object.
| Left | Right | Stereo | Reference | |
|---|---|---|---|---|
| Focal Length (mm) | 1.89 | 1.93 | 3 | |
| First-order radial distortion (mm^-2) | -0.244 | -0.240 | ||
| Baseline (mm) | 32.50 | 33 | ||
| Camera-cube distance (mm) | 251.0 | 233 |
In classic camera calibration, photographs of an object with known geometry (a calibration object) are used to estimate the parameters using optimization techniques.
The most popular method for low-cost camera calibration is Zhang's technique[2] - which uses several photographs to calibrate the camera. This can be problematic in some applications (for example, when battery life is limited). In contrast, Tsai's technique[1] uses a single photograph. A downside to this approach is that the points used in Tsai calibration cannot lie on the same plane, so the calibration object must be more complex than the simple checkerboards typically used in Zhang calibration.
To estimate the parameters of the model, a 2-stage process is used. First, the parameters of a linear pinhole camera model are estimated using a linear optimisation process (Singular Value Decomposition). In the second stage, the model is extended to estimate the nonlinear lens distortion parameters. Parameters for the resulting model can then be found using a nonlinear optimisation process (gradient descent). The resulting algorithm is much faster than the traditional methods used in photogrammetry that simultaneously optimize all the parameters using nonlinear methods.
- Python 2.x
- NumPy (Math library)
- Matplotlib (2D/3D plotting library)
python main.py > output/output.txt
- R. Tsai, "A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses," in IEEE Journal on Robotics and Automation, vol. 3, no. 4, pp. 323-344, August 1987. web: ieee.org sci-hub.io doi: 10.1109/JRA.1987.1087109
- Z. Zhang, "A Flexible New Technique for Camera Calibration," in IEEE Transactionson Pattern Analysis and Machine Intelligence, Vol. 22, No. 11, pp. 1330-1334, 2000. web: microsoft.com sci-hub.io doi: 10.1109/34.888718
- W. Li, T. Gee, H. Friedrich, and P. Delmas, “A practical comparison between Zhang’s and Tsai’s calibration approaches,” in Proceedings of the 29th International Conference on Image and Vision Computing New Zealand, ser. IVCNZ ’14, Hamilton, New Zealand: ACM, pp. 166–171, 2014. ISBN: 978-1-4503-3184-5. web: acm.org sci-hub.io doi: 10.1145/2683405.2683443
- Manuel E. L. Fernandez, Lucas Teixeira and Marcelo Gattass, ANSI C Implementation of Classical Camera Calibration Algorithms: Tsai and Zhang
- For calibration without any special objects in the scene, see Camera auto-calibration