- Forth VM that supports tensor calculus and Convolution Neural Network with dynamic parallelism in CUDA
| version | feature | stage | description | conceptual comparable |
|---|---|---|---|---|
| 1.0 | float | production | extended eForth with F32 float | Python |
| 2.0 | matrix | production | + vector and matrix objects | NumPy |
| 2.2 | lapack | production | + linear algebra methods | SciPy |
| 3.0 | CNN | beta | + Machine Learning with autograd | Torch |
| 3.2 | GAN | alpha | + Generative Adversarial Net | PyTorch.GAN |
| 4.0 | Transformer | developing | add Transformer ops | PyTorch.Transformer |
| 4.2 | Retentive | analyzing | add RetNet ops | PyTorch.RetNet |
Compiled programs run fast on Linux. On the other hand, command-line interface and shell scripting tie them together in operation. With interactive development, small tools are built along the way, productivity usually grows with time, especially in the hands of researchers.
Niklaus Wirth: Algorithms + Data Structures = Programs
- Too much on Algorithms - most modern languages, i.e. OOP, abstraction, template, ...
- Too focused on Data Structures - APL, SQL, ...
Numpy kind of solves both. So, for AI projects today, we use Python mostly. However, when GPU got involved, to enable processing on CUDA device, say with Numba or the likes, mostly there will be a behind the scene 'just-in-time' transcoding to C/C++ followed by compilation then load and run. In a sense, your Python code behaves like a Makefile which requires compilers/linker available on the host box. Common practice for code analysis can only happen at the tail-end after execution. This is usually a long journey. After many coffee breaks, we tweak the Python code and restart again. To monitor progress or catch any anomaly, scanning the intermittent dump become a habit which probably reminisce the line-printer days for seasoned developers. So much for 70 years of software engineering progress.
Forth language encourages incremental build and test. Having a 'shell', resides in GPU, that can interactively and incrementally develop/run each AI layer/node as a small 'subroutine' without dropping back to host system might better assist building a rapid and accurate system. The rationale is not unlike why the NASA probes sent into space are equipped with Forth chips. On the flipped side, with this kind of CUDA kernel code, some might argue that the branch divergence could kill the GPU. Well, there's always space for improving. Also, the performance of the 'shell scripts' themselves is never really the point. So, here we are!
tensor + Forth = tensorForth!
More details to come but here are some samples of tensorForth in action
-
Benchmarks (on MNIST)
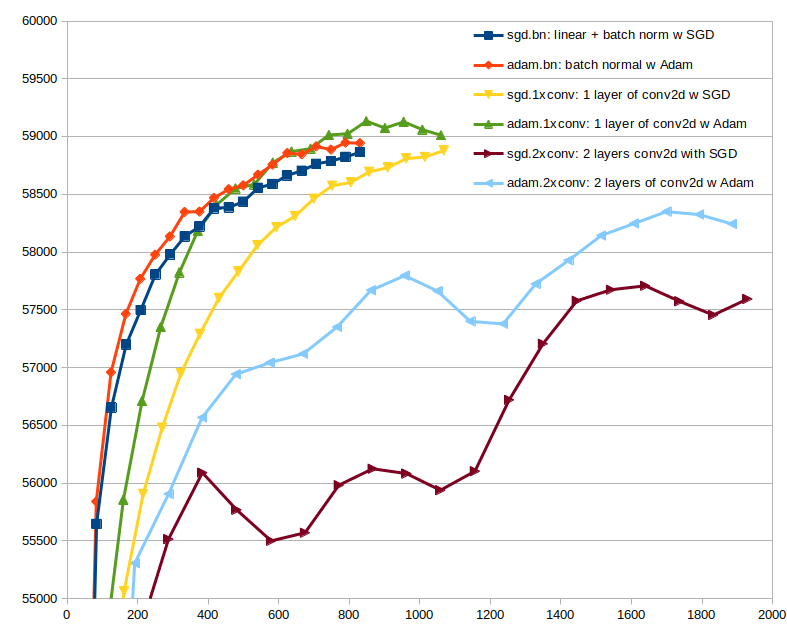
Different Neural Network Models Different Gradient Descent Methods 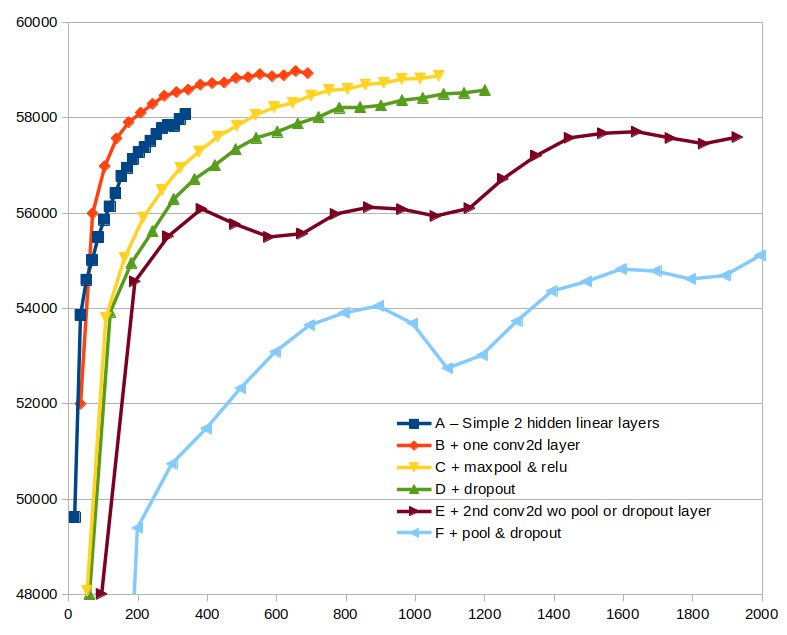
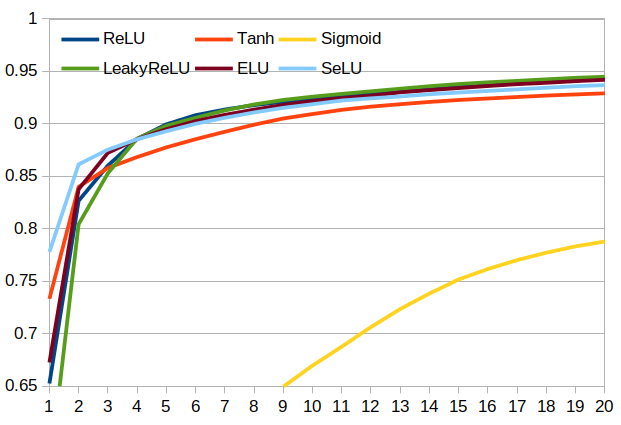
2D Convolution vs Linear+BatchNorm Effectiveness of Different Activations 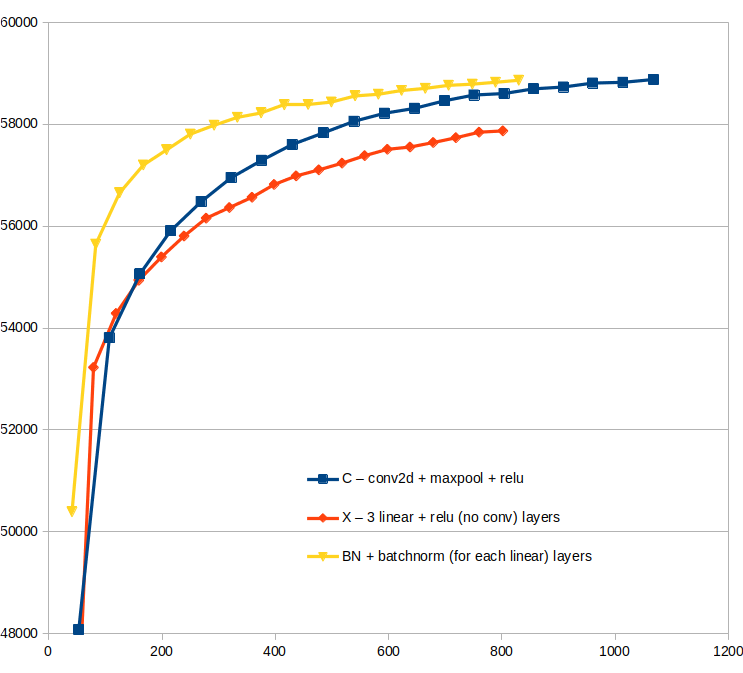
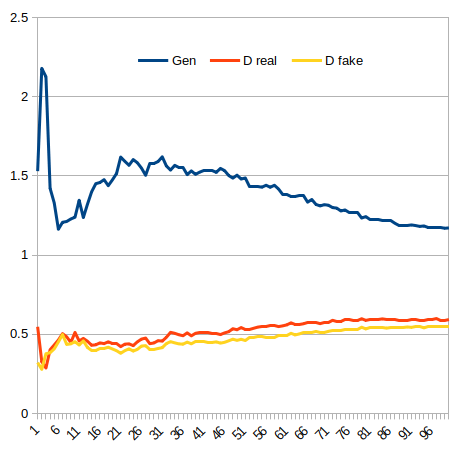
Generative Adversarial Network (MNIST) Generator & Discriminator Losses 
GPU, behaves like a co-processor or a DSP chip. It has no OS, no string support, and runs its own memory. Most of the available libraries are built for host instead of device i.e. to initiate calls from CPU into GPU but not the other way around. So, to be interactive, a memory manager, IO, and syncing with CPU are things needed to be had. It's pretty much like creating a Forth from scratch for a new processor as in the old days.
Since GPUs have good compiler support nowadays and I've ported the latest eForth to lambda-based in C++, pretty much all words can be transferred straight forward. However, having FP32 or float32 as my basic data unit, so later I can morph them to FP16, or even fixed-point, there are some small stuffs such as addressing and logic ops that require some attention.
The codebase will be in C for my own understanding of the multi-trip data flows. In the future, the class/methods implementation can come back to Forth in the form of loadable blocks so maintainability and extensibility can be utilized as other self-hosting systems. It would be amusing to find someone brave enough to work the NVVM IR or even PTX assembly into a Forth that resides on GPU micro-cores in the fashion of GreenArray, or to forge an FPGA doing similar kind of things.
In the end, languages don't really matter. It's the problem they solve. Having an interactive Forth in GPU does not mean a lot by itself. However by adding vector, matrix, linear algebra support with a breath of APL's massively parallel from GPUs. Neural Network tensor ops with backprop following the path from Numpy to PyTorch, plus the cleanness of Forth, it can be useful one day, hopefully!
> ten4 # enter tensorForth
tensorForth 2.0
\ GPU 0 initialized at 1800MHz, dict[1024], vmss[64*1], pmem=48K, tensor=1024M
2 3 matrix{ 1 2 3 4 5 6 } \ create a 2x3 matrix
<0 T2[2,3]> ok \ 2-D tensor shown on top of stack (TOS)
dup \ create a view of the matrix
<0 T2[2,3] t[2,3]> ok \ view shown in lower case
. \ print the matrix (destructive as in Forth)
matrix[2,3] = {
{ +1.0000 +2.0000 +3.0000 }
{ +4.0000 +5.0000 +6.0000 } }
<0 T2[2,3]> ok \ original matrix still on TOS
3 2 matrix ones \ create a 3x2 matrix, fill it with ones
<0 T2[2,3] T2[3,2]> ok \ now we have two matrices on stack
dup . \ see whether it is filled with one indeed
matrix[3,2] = {
{ +1.0000 +1.0000 }
{ +1.0000 +1.0000 }
{ +1.0000 +1.0000 } }
@ \ multiply them 2x3 @ 3x2
<0 T2[2,3] T2[3,2] T2[2,2]> ok \ 2x2 resultant matrix shown on TOS
. \ print the new matrix
matrix[2,2] = {
{ +6.0000 +6.0000 }
{ +15.0000 +15.0000 } }
<0 T2[2,3] T2[3,2]> ok
bye \ exit tensorForth
<0> ok
tensorForth 2.0 done.
1024 2048 matrix rand \ create a 1024x2048 matrix with uniform random values
<0 T2[1024,2048]> ok
2048 512 matrix ones \ create another 2048x512 matrix filled with 1s
<0 T2[1024,2048] T2[2048,512]> ok
@ \ multiply them and resultant matrix on TOS
<0 T2[1024,2048] T2[2048,512] T2[1024,512]> ok
2048 /= . \ scale down and print the resultant 1024x512 matrix
matrix[1024,512] = { \ in PyTorch style (edgeitem=3)
{ +0.4873 +0.4873 +0.4873 ... +0.4873 +0.4873 +0.4873 }
{ +0.4274 +0.4274 +0.4274 ... +0.4274 +0.4274 +0.4274 }
{ +0.5043 +0.5043 +0.5043 ... +0.5043 +0.5043 +0.5043 }
...
{ +0.5041 +0.5041 +0.5041 ... +0.5041 +0.5041 +0.5041 }
{ +0.5007 +0.5007 +0.5007 ... +0.5007 +0.5007 +0.5007 }
{ +0.5269 +0.5269 +0.5269 ... +0.5269 +0.5269 +0.5269 } }
<0 T2[1024,2048] T2[2048,512]> ok
: mx \ now let's define a word 'mx' for benchmark loop
clock >r \ keep the init time (in msec) on return stack
for @ drop next \ loops of matrix multiplication
clock r> - ; \ time it (clock1 - clock0)
<0 T2[1024,2048] T2[2048,512]> ok
999 mx \ now try 1000 loops
<0 T2[1024,2048] T2[2048,512] 3.938+04> ok \ that is 39.38 sec (i.e. ~40ms / loop)
10 28 28 1 nn.model \ create a network model (input dimensions)
0.5 10 conv2d 2 maxpool relu \ add a convolution block
0.5 20 conv2d 0.5 dropout 2 maxpool relu \ add another convolution block
flatten 49 linear \ add reduction layer to 49-feature, and
0.5 dropout 10 linear softmax \ final 10-feature fully connected output
constant md0 \ we can keep the model as a constant
md0 batchsize dataset mnist_train \ create a MNIST dataset with model batch size
constant ds0 \ keep the dataset as a constant
\ the entire CNN training framework here
: epoch ( N D -- N' ) \ one epoch thru entire training dataset
for \ loop thru dataset per mini-batch
forward \ neural network forward pass
backprop \ neural network back propagation
0.01 nn.sgd \ training with Stochastic Gradient Descent
next ; \ next mini-batch (kept on return stack)
: cnn ( N D n -- N' D ) \ run multiple epochs
for epoch ds0 rewind next ;
ds0 19 cnn drop \ put dataset as TOS, run the CNN for 20 epochs
s" tests/my_net.t4" save \ persist the trained network
- install CUDA 11.6+ on your machine
- download one of the releases from the list above to your local directory
Build on Linux
cd to your ten4 repo directory,
update root Makefile to your desired CUDA_ARCH, CUDA_CODE,
type 'make all',
if all goes well, some warnings aside, cd to tests directory,
Test v1 eForth ops
~/tests> ten4 < lesson_1.txt - for basic syntax checks
Test v2 matrix ops
~/tests> ten4 < lesson_2.txt - for matrix ops
~/tests> ten4 < lesson_3.txt - for linear algebra stuffs
Test v3 ML ops
~/tests> ten4 < lesson_4.txt - NN model forward, loss, and backprop verification - single pass
~/tests> ten4 < lesson_5.txt - MINST training, 20 epochs
Tests v3.2 GAN ops
~/tests> ten4 < lesson_6a.txt - GAN on NN single sample linear layer verification
~/tests> ten4 < lesson_6b.txt - GAN on NN multi-sample linear layer verification
~/tests> ten4 < lesson_6.txt - GAN on simple linear regression, 10 epochs
~/tests> ten4 < lesson_7.txt - GAN on MINST dataset, 100 epochs
install Eclipse
install CUDA SDK 11.6 or above for Eclipse (from Nvidia site)
create project by importing from your local repo root
exclude directories - ~/tests, ~/img
set File=>Properties=>C/C++ Build=>Setting=>NVCC compiler
+ Dialect=C++14
+ CUDA=5.2 or above (depends on your GPU)
+ Optimization=O2 or O3
\-h - list all GPU id and their properties
\-d device_id - select GPU device id
\-v verbo_level - set verbosity level 0: off (default), 1: mmu tracing on, 2: detailed trace
Machine Learning vocabularies (see doc3 for detail and examples)
nn.model (n h w c -- N) - create a Neural Network model with (n,h,w,c) input >n (N T -- N') - manually add tensor to model n@ (N n -- N T) - fetch layered tensor from model, -1 is the latest layer nn.w (N n -- N T) - query weight tensor of nth layer (0 means N/A) nn.b (N n -- N T) - query bias tensor of nth layer (0 means N/A) nn.dw (N n -- N T) - query weight gradient tensor of nth layer (0 means N/A) nn.db (N n -- N T) - query bias gradient tensor of nth layer (0 means N/A) nn.w= (N T n -- N') - set weight tensor of nth layer nn.b= (N T n -- N') - set bias tensor of nth layer network (N -- N) - display network model load (N adr len [fam] -- N') - load trained network from a given file name save (N adr len [fam] -- N) - export network as a file
dataset (n -- D) - create a dataset with batch size = n, and given name i.e. 10 dataset abc fetch (D -- D') - fetch a mini-batch from dataset on return stack rewind (D -- D') - rewind dataset internal counters (for another epoch) batchsize (D -- D b) - get input batch size of a model forward (N -- N') - execute one forward path with rs[-1] dataset, layer-by-layer in given model forward (N ds -- N') - execute one forward propagation with TOS dataset, layer-by-layer in given model backprop (N -- N') - execute one backward propagation, adding derivatives for all parameters backprop (N T -- N') - execute one backward propagation with given onehot vector broadcast (N T -- N' ) - broadcast onehot tensor into Network Model (for backprop) for (N ds -- N') - loop through a dataset, ds will be pushed onto return stack next (N -- N') - loop if any subset of dataset left, or ds is pop off return stack trainable (N f -- N') - enable/disable network trainable flag
conv2d (N -- N') - create a 2D convolution 3x3 filter, stride=1, padding=same, dilation=0, bias=0.5 conv2d (N b c -- N') - create a 2D convolution, bias=b, c channels output, with default 3x3 filter conv2d (N b c A -- N') - create a 2D convolution, bias=b, c channels output, with config i.g. Vector[5, 5, 3, 2, 1] for (5x5, padding=3, stride=2, dilation=1, bias=0.3) conv1x1 (N b c -- N') - create a 1x1 convolution, bias=b, c channels output, stride=1, padding=same, dilation=0 flatten (N -- N') - flatten a tensor (usually input to linear) linear (N b n -- N') - linearize (y = Wx + b) from Ta input to n out_features linear (N n -- N') - linearize (y = Wx), bias=0.0 from Ta input to n out_features maxpool (N n -- N') - nxn cells maximum pooling avgpool (N n -- N') - nxn cells average pooling minpool (N n -- N') - nxn cell minimum pooling dropout (N p -- N') - zero out p% of channel data (add noise between data points) upsample (N n -- N') - upsample to nearest size=n, 2x2 and 3x3 supported upsample (N m n -- N') - upsample size=n, 2x2 and 3x3 supported, method=[0 nearest, 1=linear, 2=bilinear, 3=cubic batchnorm (N -- N') - batch normal layer with default momentum=0.1 batchnorm (N m -- N') - batch normal with momentum=m
tanh (N -- N') - add tanh layer to network model relu (N -- N') - add Rectified Linear Unit to network model sigmoid (N -- N') - add sigmoid 1/(1+exp^-z) activation to network model, used in binary cross entropy selu (N -- N') - add Selu alpha(exp-1) activation to network model leakyrelu (N a -- N') - add leaky ReLU with slope=a leu (N a -- N') - add exponential linear unit alpha=a softmax (N -- N') - add probability vector exp(x)/sum(exp(x)) to network model, feeds loss.ce, used in multi-class logsoftmax (N -- N') - add probability vector x - log(sum(exp(x))) to network model, feeds loss.nll, used in multi-class
loss.mse (N Ta -- N Ta n) - mean squared error, takes output from linear layer loss.bce (N Ta -- N Ta n) - binary cross-entropy, takes output from sigmoid activation loss.ce (N Ta -- N Ta n) - cross-entropy, takes output from softmax activation loss.nll (N Ta -- N Ta n) - negative log likelihood, takes output from log-softmax activation nn.loss (N Ta -- N Ta n) - auto select between mse, bce, ce, nll based on last model output layer nn.zero (N -- N') - manually zero gradient tensors nn.sgd (N p -- N') - apply SGD(learn_rate=p, momentum=0.0) model back propagation nn.sgd (N p m -- N') - apply SGD(learn_rate=p, momentum=m) model back propagation nn.adam (N a -- N') - apply Adam backprop alpha=a, default b1=0.9, b2=0.999 nn.adam (N a b1 -- N') - apply Adam backprop alpha=a, beta1=b1, default beta2=0.999 nn.adam (N a b1 b2 -- N') - apply Adam backprop alpha=a, beta1=b1, beta2=b2 nn.zero (N -- N') - reset momentum tensors nn.onehot (N -- N T) - get cached onehot vector from a model nn.hit (N -- N n) - get number of hit (per mini-batch) of a model
Tensor Calculus vocabularies (see doc2 for detail and examples)
vector (n -- T1) - create a 1-D array and place on top of stack (TOS)
matrix (h w -- T2) - create 2-D matrix and place on TOS
tensor (n h w c -- T4) - create a 4-D NHWC tensor on TOS
vector{ (n -- T1) - create 1-D array from console stream
matrix{ (h w -- T2) - create a 2-D matrix from console stream
view (Ta -- Ta Va) - create a view (shallow copy) of a tensor
copy (Ta -- Ta Ta') - duplicate (deep copy) a tensor on TOS
dup (Ta -- Ta Ta) - create a reference of a tensor on TOS over (Ta Tb -- Ta Tb Ta) - create a reference of the 2nd item (NOS) 2dup (Ta Tb -- Ta Tb Ta Tb) 2over (Ta Tb Tc Td -- Ta Tb Tc Td Ta Tb)
. (dot) (Ta -- Ta) - print a vector, matrix, or tensor . (dot) (Va -- Va) - print a view of a tensor
flatten (Ta -- T1a') - reshape a tensor or view to 1-D array reshape2 (Ta -- T2a') - reshape to a 2-D matrix view reshape4 (Ta -- T4a') - reshape to a 4-D NHWC tensor or view same_shape? (Ta Tb -- Ta Tb T/F) - check whether Ta and Tb are the same shape
zeros (Ta -- Ta') - fill tensor with zeros
ones (Ta -- Ta') - fill tensor with ones
gradfill (Ta -- Ta') - gradient fill elements from 0 to 1
full (Ta n -- Ta') - fill tensor with number on TOS
eye (Ta -- Ta') - fill diag with 1 and other with 0
rand (Ta -- Ta') - fill tensor with uniform random numbers
randn (Ta -- Ta') - fill tensor with normal distribution random numbers
={ (Ta -- Ta') - fill tensor with console input from the first element
={ (Ta n -- Ta') - fill tensor with console input starting at n'th element
t@ (T i -- T n) - fetch ith element from a tensor (in NHWC order) t! (T i n -- T') - store n into ith element of a tensor (in NHWC order) slice (Ta i0 i1 j0 j1 -- Ta Ta') - numpy.slice[i0:i1,j0:j1,]
+ (Ta Tb -- Ta Tb Tc) - tensor element-wise addition Tc = Ta + Tb + (Ta n -- Ta n Ta') - tensor-scalar addition (broadcast) Ta' = Ta + n + (n Ta -- n Ta Ta') - scalar-tensor addition (broadcast) Ta' = Ta + n - (Ta Tb -- Ta Tb Tc) - tensor element-wise subtraction Tc = Ta - Tb - (Ta n -- Ta n Ta') - tensor-scalar subtraction (broadcast) Ta' = Ta - n - (n Ta -- n Ta Ta') - tensor-scalar subtraction (broadcast) Ta' = n - Ta @ (Ta Tb -- Ta Tb Tc) - matrix-matrix inner product Tc = Ta @ Tb, i.e. matmul @ (Ta Ab -- Ta Ab Ac) - matrix-vector inner product Ac = Ta @ Ab @ (Aa Ab -- Aa Ab n) - vector-vector inner product n = Aa @ Ab, i.e. dot * (Ta Tb -- Ta Tb Tc) - tensor-tensor element-wise multiplication Tc = Ta * Tb * (Ta Ab -- Ta Ab Ta') - matrix-vector multiplication Ta' = Ta * column_vector(Ab) * (Ta n -- Ta n Ta') - tensor-scalar multiplication Ta' = n * Ta, i.e. scale up * (n Ta -- n Ta Ta') - scalar-tensor multiplication Ta' = n * Ta, i.e. scale up / (Ta Tb -- Ta Tb Tc) - tensor-tensor element-wise divide Tc = Ta / Tb / (Ta n -- Ta n Ta') - tensor-scalar scale down Ta' = 1/n * Ta sum (Ta -- Ta n) - sum all elements of a tensor avg (Ta -- Ta n) - average of all elements of a tensor max (Ta -- Ta n) - max of all elements of a tensor min (Ta -- Ta n) - min of all elements of a tensor
abs (Ta -- Ta') - absolute Ta' = abs(Ta) exp (Ta -- Ta') - exponential Ta' = exp(Ta) ln (Ta -- Ta') - natural log Ta' = ln(Ta) log (Ta -- Ta') - logrithm tanh Ta' = log(Ta) tanh (Ta -- Ta') - tanh Ta' = tanh(Ta) relu (Ta -- Ta') - ReLU Ta' = max(0, Ta) sigmoid (Ta -- Ta') - Sigmoid Ta' = 1/(1+exp(-Ta)) sqrt (Ta -- Ta') - Square Root Ta' = sqrt(Ta) 1/x (Ta -- Ta') - reciprocal Ta' = 1/Ta negate (Ta -- Ta') - negate Ta' = -(Ta)
+= (Ta Tb -- Tc) - tensor element-wise addition Tc = Ta + Tb += (Ta n -- Ta') - tensor-scalar addition (broadcast) Ta' = Ta + n += (n Ta -- Ta') - scalar-tensor addition (broadcast) Ta' = Ta + n -= (Ta Tb -- Tc) - tensor element-wise subtraction Tc = Ta - Tb -= (Ta n -- Ta') - tensor-scalar subtraction (broadcast) Ta' = Ta - n -= (n Ta -- Ta') - scalar-tensor subtraction (broadcast) Ta' = n - Ta @= (Ta Tb -- Tc) - matrix-matrix inner product Tc = Ta @ Tb, i.e. matmul @= (Ta Ab -- Ac) - matrix-vector inner product Ac = Ta @ Ab @= (Aa Ab -- Ac) - vector-vector inner product n = Aa @ Ab, i.e. dot *= (Ta Tb -- Tc) - matrix-matrix element-wise multiplication Tc = Ta * Tb *= (Ta Ab -- Ac') - matrix-vector multiplication Ac' = Ta * Ab *= (Ta n -- Ta') - tensor-scalar multiplication Ta' = n * Ta *= (n Ta -- Ta') - scalar-tensor multiplication Ta' = n * Ta /= (Ta Tb -- Tc) - matrix-matrix element-wise Tc = Ta / Tb /= (Ta n -- Ta') - tensor-scalar scale down multiplication Ta' = 1/n * Ta
loss.mse (Tx Ty -- Tx') - Mean Square Loss loss.bce (Tx Ty -- Tx') - Binary Cross Entropy Loss loss.ce (Tx Ty -- Tx') - Categorical Cross Entropy Loss loss.nll (Tx Ty -- Tx') - Negative Log Likelihood Loss
matmul (Ma Mb -- Ma Mb Mc) - matrix-matrix multiplication Mc = Ma @ Mb matdiv (Ma Mb -- Ma Mb Mc) - matrix-matrix division Mc = Ma @ inverse(Mb) inverse (Ma -- Ma Ma') - matrix inversion (Gauss-Jordan with Pivot) transpose (Ma -- Ma Ma') - matrix transpose det (Ma -- Ma d) - matrix determinant (with PLU) lu (Ma -- Ma Ma') - LU decomposition (no Pivot) luinv (Ma -- Ma Ma') - inverse of an LU matrix upper (Ma -- Ma Ma') - upper triangle lower (Ma -- Ma Ma') - lower triangle with diag filled with 1s solve (Ab Ma -- Ab Ma Ax) - solve linear equation AX = B gemm (a b Ma Mb Mc -- a b Ma Mb Mc') - GEMM Mc' = a * Ma * Mb + b * Mc
save (T adr len [fam] -- T) - pickle tensor to OS file (default text mode)
- Design & Instrumentation
- Visulization via TensorBoard
- output tensor in HWC format
- util from raw to png (with STB)
- for PIL (Python Image Lib), matplotlib
- tfevents
- protobuf
- tensorflow EventWriter
- pytorch SummaryWriter
- pytorch TensorBoard writer
- Ollama
- Review. Local LLM environment with pre-train model.
- GGML Tensor library. Host-oriented, review kernel code.
- GGUF. Optimized for GPU, cross-platform, structured model storage.
- Visulization via TensorBoard
- VM
- review CUDA HostFunc callback (requires CUDA Stream)
- review CUDA dynamic Graph
- review CUB (now part of CCCL) again
- inter-VM communication (via CUDA stream)
- inter-VM loader (from VM->VM)
- free_tensor as linked-list (instead of an array)
- Model
- GAN
- AC-GAN
- use pre-trained model, i.e. transfer learning
- torch.eval() i.e. normalize using running stat, disable dropout (vs torch.train())
- new layers
- add Swish, Mish
- add Transposed Convolution. Less used now b/c it creates checkerboard pattern, see https://distill.pub/2016/deconv-checkerboard/)
- Transformer
- Review
- CNN vs ViT (good ref paper)
- seq2seq vs Transformer
- Retentitive Network
- Intro
- Code
- transformer
- position encoding
- python
- pytorch
- pytorch
- llama.cpp
- llama2.c. 700-line C. Tiny Llama trainning + inferencing.
- Review
- New Layers
- 1x1 Convolution (resize #channel)
- residual net i.e. ResNet
- branch & concatenate (i.e Inception in GoogLeNet)
- GNN - dynamic graph with VMs. Value proposition.
- Multi-Domain, i.e. MDNet
- GAN
- Data
- add loader plug-in API - CIFAR
- add K-fold sampler
- data API - Python(cffi), Ruby(FFI)
- Refactor
- study Scikit-learn (discrete functions)
- study JAX
- JIT (XLA)
- auto parallelization (pmap)
- auto vectorization (vmap)
- auto diff (grad), diffrax (RK4, Dormand-Prince)
- check namespace
- warp-level collectives (study libcu++, MordenGPU for kernel)
- Tuning
- Graph (CUDA 10.x) - host-only, to reduce repetitive launch overhead
- HMM (CUDA 12.2) - unify CPU-GPU memory allocation
- CUB (CUDA 12.4) - warp/block/device-wide collective primitives
- CUDA binary, study possibility for VM in assembly https://docs.nvidia.com/cuda/cuda-binary-utilities/index.html#instruction-set-reference
- Review NVBits
- cuobjdump
- cudisasm
- Language consistancy
- compare to APL https://www.jsoftware.com/papers/APLDictionary.htm
- compare to J, (rank & axis ops)
- Model
- Latent Diffusion, Stable Diffusion. Pre-trained only?
- RNN, lost to Transformer.
- Data
- NCHW tensor format support (as in PyTorch)
- loader - .petastorm, .csv (available on github)
- model persistence - .npy, .petastorm, hdf5
- integrate ONNX
- Visualization
- TensorBoard
- output tensor in HWC format
- util from raw to png (with STB)
- for PIL (Python Image Lib), matplotlib
- tfevents
- protobuf
- tensorflow EventWriter
- pytorch SummaryWriter
- pytorch TensorBoard writer
- nvdiffrast https://nvlabs.github.io/nvdiffrast/
- OpenGL/WASM
- TensorBoard
- 3rd-party lib Integration
- integrate CUB, CUTLASS (utilities.init, gemm_api) - slow, later
- pre-processor (DALI) + GPUDirect - heavy, later
- calling API - Python(cffi), Ruby(FFI)
Release 1.0 features
- Dr. Ting's eForth words with F32 as data unit, U16 instruction unit
- Support parallel Forth VMs
- Lambda-based Forth microcode
- Memory management unit handles dictionary, stack, and parameter blocks in CUDA
- Managed memory debug utilities, words, see, ss_dump, mem_dump
- String handling utilities in CUDA
- Light-weight vector class, no dependency on STL
- Output Stream, async from GPU to host
Release 2.0 features
- vector, matrix, tensor objects (modeled to PyTorch)
- TLSF tensor storage manager (now 4G max)
- matrix arithmetic (i.e. +, -, *, copy, matmul, transpose)
- matrix fill (i.e. zeros, ones, full, eye, random)
- matrix console input (i.e. matrix[..., array[..., and T![)
- matrix print (i.e PyTorch-style, adjustable edge elements)
- tensor view (i.e. dup, over, pick, r@)
- GEMM (i.e. a * A x B + b * C, use CUDA Dynamic Parallelism)
- command line option: debug print level control (T4_DEBUG)
- command line option: list (all) device properties
- use cuRAND kernel randomizer for uniform and standard normal distribution
Release 3.0 features
- NN model creation and persistence
- NN model batch control (feed forward, backprop w/ autograd)
- optimization - sgd
- layers - conv2d, linear, flatten
- pooling - maxpool, minpool, avgpool, dropout
- activation - relu, sigmoid, softmax, log_softmax
- loss - ce, mse, nll
- formatted data - NHWC (as in TensorFlow)
- dataset rewind
- mini-batch fetch
- dataset loader - MNIST
- OpenGL dataset Viewer
- NN model - supports GAN
- optimization - adam, sgd with momentum, grad_zero
- layers - conv1x1, upsample, batchnorm
- activation - tanh, selu, leakyrelu, elu
- loss - bce
- tensor op - std (stdvar), sqrt