In this 42 school project, we designed and implemented an algorithm to solve a special case of a maximum flow problem in graph theory.
The goal is to find the optimal flow of ants through an anthill that minimizes the number of rounds needed to traverse the anthill.
An anthill is described as a network composed of 'rooms' (graph nodes) and 'tunnels' (edges) linking the rooms together, with all ants starting and finishing at two precise rooms.
The real trouble begins when each room can welcome only one ant at a time (except for the start and end rooms).
A round ends when no more ants are able to start or move any further in the anthill.
For each round of the algorithm, an augmenting path is found, increasing the potential flow of ants through the anthill. Edmonds-Karp algorithm chooses the next augmenting path using breadth-first search (BFS). If there are multiple augmenting paths to choose from, Edmonds-Karp garantees to select the shortest path from source to sink. Once there are no remaining paths found, the algorithm ends.
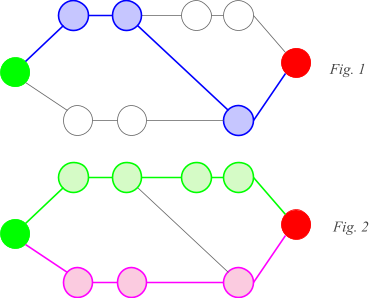
We decided to design a tweaked version of the BFS to allow backtracking on a node already included in a selected augmenting path. We were able to find more paths than with regular Edmonds-Karp, thus improving the algorithm efficiency. Below is a case in point. The regular BFS will only find the path on Fig. 1. For a number of ants greater than 2, this is not the best solution. Our modified BFS will find the two paths on Fig. 2:
Once all the augmenting paths are found, we have to decide which paths to use in order to minimize the number of rounds given the number of ants. We consider the following :
N = total number of ants
I = total number of paths
ni = number of ants on path i
li = length of path i
Ci = cost of path i (number of lines) = ni + li - 1
min ( max (Ci : i ∀ i ∈ [0, I]) ) ⟺ min C
At the beginning, C is set to the length of the shortest path. For each incremental value of C, we try to solve the following equations system:
Σ ni = N ∀ i ∈ [0, I]
ni ≤ C - li + 1
Until a feasible solution is found, we increment C. We finally know how many ants will flow on each path.
Modified Edmonds-Karp with BFS searching for paths minimizing the lines of output
function main(options):
parse the arguments for any display options
parse the file from stdin (get ants number, rooms and tunnels)
build the graph data structure with an adjacency list with all edge's capacities at 1
if (parsing error):
print error and exit
initialize paths list to null
paths = find_paths(graph)
if (no solution is found):
print error and exit
print the file on stdout
assign each ant to a path
let the ants pass into the graph by printing one line of output for each round on stdout
display any options from arguments
function find_paths(graph):
initialize paths list to null
new_path = bfs(graph)
append new_path to paths list
reduce capacities of the new_path forward edges
increase capacities of the new_path backward edges
compute the initial lines of output using only this new_path
point to the new_path as selected_path
while (selected_path did not reach the end of the paths list):
store the previous number of paths found
new_path = bfs(graph, selected_path)
compute the new lines of output
if (the new output is minimized):
update the count of lines of output
append new_paths to paths
reduce capacities of the new_path forward edges to 0
increase capacities of the new_path backward edges to 2
point selected_path to first path
else:
discard new_path
point selected_path to next path
return (paths)
function bfs(graph, selected_path):
create a queue and add start_room
create a prev[size of graph] array to keep track of previous rooms when enqueued
while (queue is not empty):
room = dequeue(queue)
for each (neighbours of room NOT already enqueued):
if (room is NOT on selected_path AND NOT end_room):
if (neighbour is on selected_path AND NOT a start_room neighbour):
mark neighbour as visited
mark neighbour as already enqueued
update prev[neighbour] = room
select neighbour2 as the previous room of neighbour on the selected_path
enqueue(neighbour, neighbour2)
else if (neighbour is NOT visited):
enqueue(room, neighbour)
else if (room is on selected_path
AND (edge to neighbour has a capacity of 2 AND NOT start_room
|| edge to neighbour has a capacity of 1 AND NOT visited)):
enqueue(room, neighbour)
return (reconstruct_path(graph, prev))
function reconstruct_path(graph, prev):
initialize new_paths list to null
room = end_room
while (room exists):
add room to new_path list
room = prev[room]
if (the first room of new_path is start):
reset all rooms visited on the new_path
return (new_path)
else:
reset all rooms visited
return (null)
function enqueue(room, neighbour):
mark neighbour as visited
mark neighbour as already enqueued
update prev[neighbour] = room
enqueue(neighbour)
Build the libft.a static library and the lem-in binary by executing make in the cloned repo.
- Google Chrome
A map with a precise format is sent to the lem-in program as stdin input:
./lem-in [-h --help] [-a --anthill] [-p --paths] [-v --visual] < maps/demo_map
5 << ants number
##start << start room is following
r0 1 2
r1 2 3
r2 3 4
r3 4 5
r4 3 5
r5 6 7
r6 8 9
r7 7 9
##end << end room is following
r8 90 1
r0-r1 << tunnels
r1-r2
r2-r8
r0-r6
#comment << optional comments at any line
r6-r7
r1-r6
r1-r4
r4-r8
r0-r3
r3-r2
r2-r5
r5-r8
Many more examples are provided in the /maps repository.
- -h --help : Display usage
- -a --anthill : Display the anthill rooms and tunnels
- -p --paths : Display the paths found by the algorithm
- -v --visual : Display the visual in a new Google Chrome tab
The output of the program is divided in two parts:
- the file read from
stdin - one line per round (output to minimize). It represents the movements of ants with the format
LX-Y(Xbeing the ant's number andYthe room's name).
5
##start
r0 1 2
r1 2 3
r2 3 4
r3 4 5
r4 3 5
r5 6 7
r6 8 9
r7 7 9
##end
r8 90 1
r0-r1
r1-r2
r2-r8
r0-r6
r6-r7
r1-r6
r1-r4
r4-r8
r0-r3
r3-r2
r2-r5
r5-r8
L1-r3 L2-r1 << round 0
L1-r2 L2-r4 L3-r3 L4-r1 << round 1
L1-r8 L2-r8 L3-r2 L4-r4 L5-r3 << round 2
L3-r8 L4-r8 L5-r2 << round 3
L5-r8 << round 4
Antoine Gelloz | Elora Kelkel |