This is a comprehensive Java implementation of my algorithm for rolling binary trees, which takes a binary tree as input and rolls it in linear time, as described in this paper. Common design patterns and best practices are followed, including the use of generics, static factory methods, the visitor pattern, the strategy pattern, etc. A complete suite of unit and integration tests is included.
This is a Maven project, so it can easily be imported into an existing Java application (e.g., via jitpack.io) and used as a library. For example, to make it a dependency of an existing Maven project, simply add the following to your pom.xml file:
<repositories>
<repository>
<id>jitpack.io</id>
<url>https://jitpack.io</url>
</repository>
</repositories>
<dependencies>
<dependency>
<groupId>com.github.gtanev</groupId>
<artifactId>binary-tree-roll-java</artifactId>
<version>1.0.0</version>
</dependency>
</dependencies>The easiest way to construct a binary tree is to provide a list of values to the BinaryTree.of static factory method. The method accepts a variable number of arguments, which can be either values of the tree nodes or null, to indicate the absence of a node. The values are added to the tree in a breadth-first fashion, starting from the root node and proceeding level by level, from left to right.
A BinaryTree instance can be traversed with one of the predefined visitors, which implement the Visitor interface and accept a Consumer as a constructor argument. The Consumer defines the action to be performed for each node in the tree, in the order specified by the visitor. The PreorderVisitor, InorderVisitor, and PostorderVisitor classes implement the preorder, inorder, and postorder traversal algorithms, respectively. A lambda expression can be used to define the visitor action.
The RollStrategyFactory class provides a way to obtain one of four possible roll strategies, which can be used to roll a binary tree in either a clockwise or a counterclockwise direction, in either a mutable (mutating) or an immutable (non-mutating) fashion.
The RollStrategyFactory.create factory method creates a mutable roll strategy, while the RollStrategyFactory.createImmutable factory method creates an immutable roll strategy. Both methods accept a RollDirection enum value argument, which can be either CLOCKWISE or COUNTERCLOCKWISE, to indicate the direction in which the tree should be rolled. Both factory methods return a RollStrategy instance.
To roll a binary tree, the RollStrategy instance should be passed as an argument to the BinaryTree.roll method, which returns the rolled tree. If the strategy is immutable, a new tree will be created and returned, while the original tree will remain unchanged. If the strategy is mutable, the original tree will be mutated and returned.
Below is a simple example of how this library can be used to construct a binary tree, roll it, and print the results to the standard output stream.
// Create a binary tree
var tree = BinaryTree.of(1, 2, 3, null, null, 4, 5, null, null, 6);
// Instantiate a printer with the standard output stream
var printer = new BinaryTreePrinter<Integer>(System.out);
// Print the tree and its traversals
printer.println("Original tree:\n");
printer.printTree(tree);
printer.printPreorder(tree);
printer.printInorder(tree);
printer.printPostorder(tree);
// Roll the tree counterclockwise
tree.roll(RollStrategyFactory.create(RollDirection.COUNTERCLOCKWISE));
// Print the rolled tree and its traversals
printer.println("\nRolled tree:\n");
printer.printTree(tree);
printer.printPreorder(tree);
printer.printInorder(tree);
printer.printPostorder(tree);Original tree:
5 ————┐
│ 6
3 ————┤
│ 4
1 ————┤
2
1 2 3 4 5 6 Preorder
2 1 4 3 6 5 Inorder
2 4 6 5 3 1 Postorder
Rolled tree:
6
5 ————┤
│ 4
3 ————┤
│ 2
1 ————┘
5 3 1 2 4 6 Preorder
1 2 3 4 5 6 Inorder
2 1 4 3 6 5 Postorder
The following example demonstrates how to use the predefined visitors to traverse a binary tree, and how to use lambda expressions to define a custom visitor action.
// Create a binary tree
var tree = BinaryTree.of('T', 'E', 'X', 'A', 'R', null, null, null, 'C', 'H');
// Print the tree to the standard output stream
new BinaryTreePrinter<Character>(System.out).printTree(tree);
// Initialize an empty list
var nodeValues = new ArrayList<Character>();
// Perform an inorder traversal of the tree and add the node values to the list
tree.traverse(new InorderVisitor<>(node -> nodeValues.add(node.getValue())));
// Check if the list is sorted to determine if the tree is a binary search tree
boolean isBST = nodeValues.stream().sorted().toList().equals(nodeValues);
// Print the result to the standard output stream
System.out.println(isBST ? "This tree is a BST" : "This tree is not a BST"); X
T ————┤
│ R ————┐
│ │ H
E ————┤
│ C
A ————┘
This tree is a BST
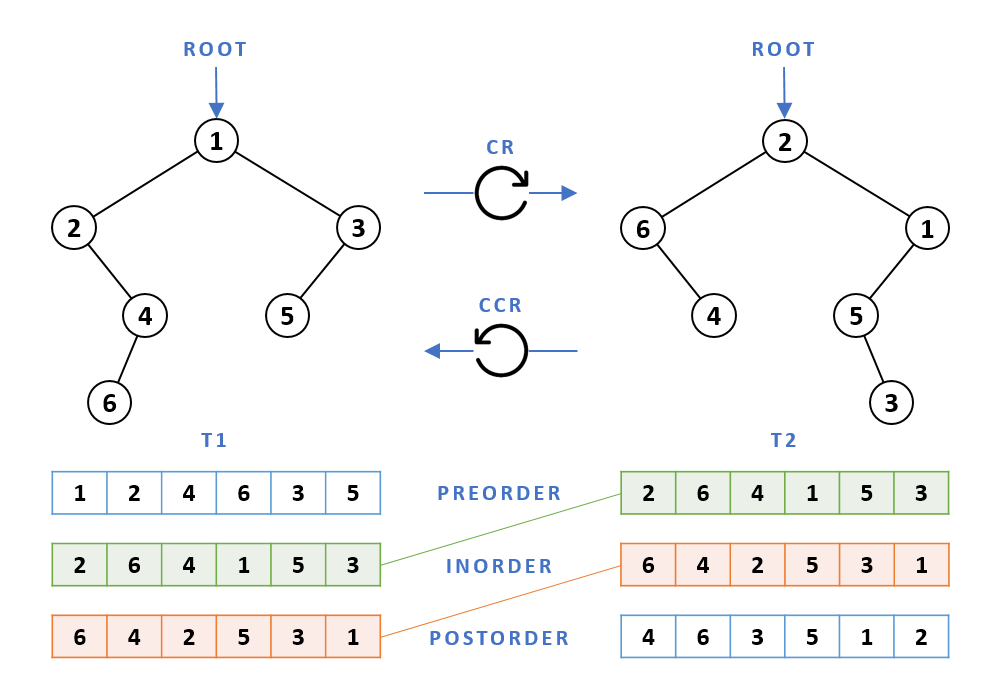
Binary tree roll is an operation which modifies the structure of a binary tree in such a manner that, when visualized, the newly obtained structure appears to be rolled at a 90-degree angle, either in a clockwise or a counterclockwise direction. Consequently, there are two distinct variants of the roll operation — clockwise roll (CR) and counterclockwise roll (CCR).
A defining property of the roll operation is that the depth-first traversals of the rolled binary tree are uniquely transposed versions of the traversals of the original tree. Formally, we can define the CR and CCR roll functions in terms of the preorder, inorder, and postorder traversals of the original (T1) and the rolled (T2) tree, as follows:
- CR(T1) = T2 ⇔ inorder(T1) = preorder(T2) & postorder(T1) = inorder(T2)
- CCR(T1) = T2 ⇔ preorder(T1) = inorder(T2) & inorder(T1) = postorder(T2)
From this definition, it follows that the CR and CCR roll operations are inverse to each other, i.e., CR(CCR(T)) = T and CCR(CR(T)) = T. Furthermore, the roll operation is non-idempotent, i.e., CR(T) ≠ CR(CR(T)) and CCR(T) ≠ CCR(CCR(T)), except in the case of a single-node binary tree.
def CCR(root, parent = null)
if root != null
if root.right != null
CCR(root.right, parent)
root.right.left = root
root.right = null
else if parent != null
parent.right = root
parent.left = null
if root.left != null
CCR(root.left, root)
The roll operation is best represented as a recursive algorithm that takes a binary tree as input and mutates its structure in place. The algorithm traverses the tree in a (reverse) inorder manner, removing existing and creating new links between the nodes as it goes. As a result, it produces a modified version of the original tree in accordance with the definition of the roll operation. A special parameter parent is used to anchor subtrees constructed during the recursive traversal to their target parent nodes.
The running time of this algorithm is linear or Θ(𝑛) analogous to the linear traversal it performs, and its space complexity is proportional to the height of the given binary tree as the call stack grows up to ℎ + 1 frames, i.e., Θ(𝑛) in the worst case (for ℎ = 𝑛 - 1) and Θ(log₂𝑛) in the best case (for ℎ = ⌊log₂𝑛⌋).
Applying the roll operation successively in a single direction on any binary tree, results in a sequential pass through a unique subset of all possible binary tree topologies of that tree's size, until the topology of the initial tree is eventually reached. In some cases, the initial tree can be reached in a single pass, while in other cases, the number of passes can be up to 𝑛 (the number of nodes in the tree). This is because some trees are topologically identical but different in terms of the positions (or values) of their nodes.
For example, rolling the tree pictured below produces 6 distinct topological permutations, while the number of unique trees is
6 * 𝑛 = 24.
Click to expand or collapse example
1 ————┐
│ 4
2 ————┤
3
[1, 2, 3, 4] Preorder
[3, 2, 4, 1] Inorder
[3, 4, 2, 1] Postorder
1
2 ————┤
│ 4
3 ————┘
[3, 2, 4, 1] Preorder
[3, 4, 2, 1] Inorder
[4, 1, 2, 3] Postorder
3 ————┐
│ 2 ————┐
│ │ 1
4 ————┘
[3, 4, 2, 1] Preorder
[4, 1, 2, 3] Inorder
[1, 2, 4, 3] Postorder
3
4 ————┤
│ 2
1 ————┘
[4, 1, 2, 3] Preorder
[1, 2, 4, 3] Inorder
[2, 1, 3, 4] Postorder
4 ————┐
│ 3
1 ————┤
2
[1, 2, 4, 3] Preorder
[2, 1, 3, 4] Inorder
[2, 3, 4, 1] Postorder
1 ————┐
│ │ 4
│ 3 ————┘
2 ————┘
[2, 1, 3, 4] Preorder
[2, 3, 4, 1] Inorder
[4, 3, 1, 2] Postorder
----------------------------------------
2 ————┐
│ 1
3 ————┤
4
[2, 3, 4, 1] Preorder
[4, 3, 1, 2] Inorder
[4, 1, 3, 2] Postorder
2
3 ————┤
│ 1
4 ————┘
[4, 3, 1, 2] Preorder
[4, 1, 3, 2] Inorder
[1, 2, 3, 4] Postorder
4 ————┐
│ 3 ————┐
│ │ 2
1 ————┘
[4, 1, 3, 2] Preorder
[1, 2, 3, 4] Inorder
[2, 3, 1, 4] Postorder
4
1 ————┤
│ 3
2 ————┘
[1, 2, 3, 4] Preorder
[2, 3, 1, 4] Inorder
[3, 2, 4, 1] Postorder
1 ————┐
│ 4
2 ————┤
3
[2, 3, 1, 4] Preorder
[3, 2, 4, 1] Inorder
[3, 4, 1, 2] Postorder
2 ————┐
│ │ 1
│ 4 ————┘
3 ————┘
[3, 2, 4, 1] Preorder
[3, 4, 1, 2] Inorder
[1, 4, 2, 3] Postorder
----------------------------------------
3 ————┐
│ 2
4 ————┤
1
[3, 4, 1, 2] Preorder
[1, 4, 2, 3] Inorder
[1, 2, 4, 3] Postorder
3
4 ————┤
│ 2
1 ————┘
[1, 4, 2, 3] Preorder
[1, 2, 4, 3] Inorder
[2, 3, 4, 1] Postorder
1 ————┐
│ 4 ————┐
│ │ 3
2 ————┘
[1, 2, 4, 3] Preorder
[2, 3, 4, 1] Inorder
[3, 4, 2, 1] Postorder
1
2 ————┤
│ 4
3 ————┘
[2, 3, 4, 1] Preorder
[3, 4, 2, 1] Inorder
[4, 3, 1, 2] Postorder
2 ————┐
│ 1
3 ————┤
4
[3, 4, 2, 1] Preorder
[4, 3, 1, 2] Inorder
[4, 1, 2, 3] Postorder
3 ————┐
│ │ 2
│ 1 ————┘
4 ————┘
[4, 3, 1, 2] Preorder
[4, 1, 2, 3] Inorder
[2, 1, 3, 4] Postorder
----------------------------------------
4 ————┐
│ 3
1 ————┤
2
[4, 1, 2, 3] Preorder
[2, 1, 3, 4] Inorder
[2, 3, 1, 4] Postorder
4
1 ————┤
│ 3
2 ————┘
[2, 1, 3, 4] Preorder
[2, 3, 1, 4] Inorder
[3, 4, 1, 2] Postorder
2 ————┐
│ 1 ————┐
│ │ 4
3 ————┘
[2, 3, 1, 4] Preorder
[3, 4, 1, 2] Inorder
[4, 1, 3, 2] Postorder
2
3 ————┤
│ 1
4 ————┘
[3, 4, 1, 2] Preorder
[4, 1, 3, 2] Inorder
[1, 4, 2, 3] Postorder
3 ————┐
│ 2
4 ————┤
1
[4, 1, 3, 2] Preorder
[1, 4, 2, 3] Inorder
[1, 2, 3, 4] Postorder
4 ————┐
│ │ 3
│ 2 ————┘
1 ————┘
[1, 4, 2, 3] Preorder
[1, 2, 3, 4] Inorder
[3, 2, 4, 1] Postorder
----------------------------------------
1 ————┐
│ 4
2 ————┤
3
[1, 2, 3, 4] Preorder
[3, 2, 4, 1] Inorder
[3, 4, 2, 1] Postorder
A detailed analysis of this algorithm can be found at: https://ieeexplore.ieee.org/document/8011115.