A Levenshtein Distance implementation using C++ with a dynamic programming approach.
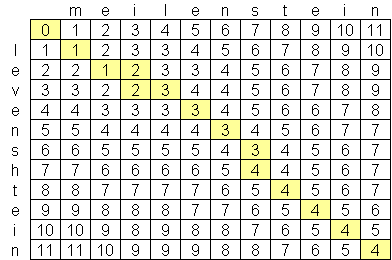
The Levenshtein algorithm (also called Edit-Distance) calculates the least number of edit operations that are necessary to modify one string to obtain another string. One way of calculating this is by the dynamic programming approach. A matrix is initialized measuring in the (m,n)-cell the Levenshtein distance between the m-character prefix of one with the n-prefix of the other word. The matrix can be filled from the upper left to the lower right corner. Each jump horizontally or vertically corresponds to an insert or a delete, respectively. The cost is set to 1 for each of the operations. The diagonal jump can cost either one, if the two characters in the row and column do not match or 0, if they do. Each cell always minimizes the cost locally. This way the number in the lower right corner is the Levenshtein distance between both words. Here is an example that features the comparison of "meilenstein" and "levenshtein":
Thus, the Levenshtein distance in this case is 4.
There are two possible paths through the matrix that actually produce the least cost solution. Namely
"=" Match; "o" Substitution; "+" Insertion; "-" Deletion
Feel free to contribute with corrections, optimizations, etc. There are no strict guidelines on how one should contribute.
This project is licensed under the MIT License - see the LICENSE file for details.