Simplest euclidean rhythm implementation, explained

Euclidean rhythms are a popular way of algorithmically creating natural-sounding rhythms, particularly in the Eurorack modular synth scene. One reason why they are popular is that many fundamental rhythms of music from different cultures are in fact euclidean, as noted by Godfried Toussaint in an influential paper on the topic.

Essentially, a euclidean rhythm consists of a number of pulses which are distributed as evenly as possible across the length of a rhythmic cycle. There are lots of good explanations of what euclidean rhythms are on the web — recently I stumbled across this explanation on synthtopia, and thought a simple algorithm for generating euclidean rhythms would be a good tool to add to my chest.

However, while there are lots of explanations of what euclidean rhythms are, there aren’t a lot of good explanations for how to generate them. My first instinct was to take a look at the paper by Godfried Toussaint in which he initially described the concept. However, translating the descriptions and algorithms in his paper into code got pretty messy, and after several attempts at different implementations I grew frustrated, feeling that there must be a way to implement a euclidean rhythm generator with compact and conceptually simple code.

Next I looked through a lot of implementations on the web, in various languages — and again, I found lots of complicated code that was both lengthy and difficult to understand. Then I found a thread on the Max/MSP forum in which a user called 11olsen posted a Max abstraction and a code fragment showing the simplest and most elegant way of generating euclidean rhythms I have found, and which relies only on the use of addition and subtraction operations.

In the rest of this post I am going to describe the basics of the algorithm visually, and then provide example code in javascript as well as an adaption of 11olsen’s Max abstraction which is a little bit easier to understand, at least for me.

Steps, pulses, and buckets

To generate euclidean rhythms you need two variables:

1. The number of total steps in the rhythmic cycle. For musical applications this tends to be 8 or 16 for duple meters (i.e. 4/4) or 12 for triple meters (3/4 or 12/8) -- although when you are stacking multiple euclidean rhythms together it can be fun to experiment with unusual numbers of steps.

2. The number of pulses to distribute across the steps.

The essential strategy for our algorithm is to use a bucket whose size is equal to the total number of steps, and for each step in the cycle to add the number of pulses to the bucket. We will decide that a pulse has occurred when the bucket reaches or exceeds its maximum value, at which point we empty the bucket and any overflow is added back to the empty bucket.

Here it is in pseudo-code:

for (each step) { 
	bucket = bucket + numberOfPulses

	if (bucket >= totalSteps) { 
		bucket = bucket - totalSteps 
		thisStep = containsPulse
	} 
	else if (bucket < totalSteps) thisStep = noPulse
} 

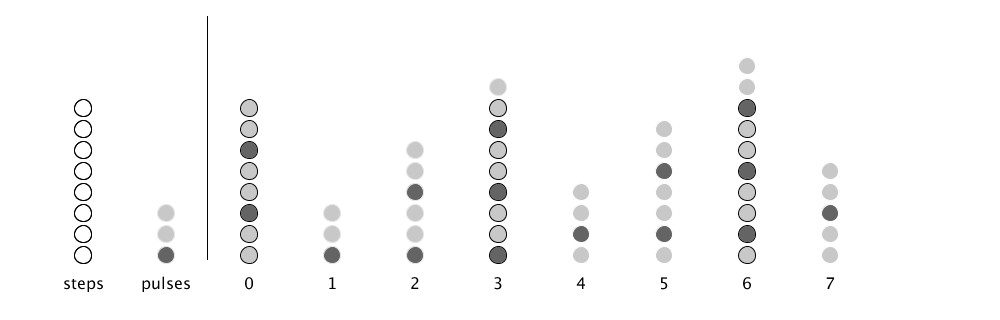
That’s it! Let’s take a look at an example of the result using 3 pulses over 8 steps:

On the left of the vertical line we can see the total number of steps and number of pulses, for reference. Note that the first circle of each pulse is a darker color, enabling us to keep track of different pulses in the bucket.

On the right of the line we see the bucket for each step. On the first step we add the number of pulses to the bucket. We do the same in the second step, for a total of six. When we add the pulses on step 3 we find that the bucket has overflowed, indicating that a pulse will occur on that step, so we indicate the pulse and then subtract the total steps from the bucket. Note the overflow from step 3 is found at the bottom of step 4, above which we again add the number of pulses. We continue this process for each step, until the final step in which we find that the bucket is exactly filled, indicating the location of our final pulse.

So, how do we know that this process generates the correct distribution? Without going into a mathematical proof, we can note that with this process the final pulse will always land on the final step, with the bucket just filled up. Essentially, the number of pulses will always divide perfectly into the number of (steps*pulses) contained in all of the buckets. This guarantees there is no remainder, which might push a pulse too early or late and thus out of a perfectly even distribution.

Rotating rhythms

One thing you might notice from our first example is that there is never a pulse on step 1 (unless the number of pulses is equal to the number of steps, which would be pointless), and in fact rhythms are always aligned so that the last pulse is on the last step. There are a couple of reasons why we might want to change this. The first is that it is common to have the first pulse of a rhythm land on the first step, and this also makes rhythms a bit easier to understand conceptually. Second, we might want to rotate a rhythm by an arbitrary number of steps - in fact it is actually pretty common for rhythms to start on the second or third pulse.

Let’s take a look at two different approaches for solving these problems. First, to make it so there is always a pulse on the first step we can  make a change to our initial algorithm: for step 1, and only step 1, we will add the number of steps to the bucket instead of adding the number of pulses. As described on line 2 of our algorithm, this will indicate a pulse on the first step, and the second step will begin with an empty bucket after the number of steps are subtracted. This is the approach taken by the algorithm as described by 11olsen. This approach demonstrates the powerful impulse to have the first pulse on the first step, in that it makes an explicit change to the code in order to force this to happen.

But we can also make this happen by implementing a more general rotation algorithm. Essentially, what we will do is generate a rhythm in the same way and rotate the rhythm a number of steps to the right, and when a step rotates past the total steps we will wrap it around to the beginning of the sequence. Here is an example with a rotation of 1:

So the end result is that if we want to force the first step to have a pulse, we will simply rotate the rhythm by 1 step.

Implementation

For our javascript implementation we utilize two functions. The first calculates the basic euclidean rhythm, given a number of steps and pulses.

//calculate a euclidean rhythm
function euclid(seq, steps,  pulses){
	seq = []; //empty array which stores the rhythm.
	//the length of the array is equal to the number of steps
	//a value of 1 for each array element indicates a pulse
	
	var bucket = 0; //out variable to add pulses together for each step
	
	//fill array with rhythm
	for( var i=0 ; i < steps ; i++){
		bucket += pulses;
		if(bucket >= steps) {
			bucket -= steps;
			seq.push(1); //'1' indicates a pulse on this beat
		} else {
			seq.push(0); //'0' indicates no pulse on this beat
		}
 	}
}

The second function carries out the rotation:

//rotate a sequence
function rotateSeq(seq, rotate){
	var output = new Array(seq.length); //new array to store shifted rhythm
	var val = seq.length - rotate;
	for( var i=0; i < seq.length ; i++){
		output[i] = seq[ Math.abs( (i+val) % seq.length) ];
	}
	return output;
}

Querying the current beat

Finally, we have a function for querying the seq array to find out if there is a pulse on the current beat:

//send triggers
function query_beat(curBeat){
	var curStep = curBeat % curSteps; //wraps beat around if it is higher than the number of steps
	return seq[curStep];
}