K Means
K-means is a clustering algorithm that aims to partition a dataset into distinct groups (clusters) based on similarity. It iteratively assigns data points to the nearest cluster centroid and updates the centroid based on the assigned points. The algorithm converges when the centroids stabilize or in simple terms, when the centers stop moving.
-
Assignment Step: Calculate the distance between each data point and the cluster centroids, and assign each data point to the nearest centroid. The distance can be computed using various distance metrics, commonly the Euclidean distance. The formula for the Euclidean distance between a data point x and a centroid c is:
$$distance(x, c) = \sqrt { \sum_{i=1}^{n} {(x_i - c_i)^2}}$$ Here,$x_i$ are the feature values of the data point$x$ , and$c_i$ are the feature values of the centroid$c$ . -
Update Step: Recalculate the centroids by taking the average of the feature values of all the data points assigned to each centroid. The formula for updating the centroid c is:
$$c_i = \frac {1}{N_i} * \sum_{j=1}^{N_i} {(x_j)}$$ Here,$c_i$ represents the updated centroid, Ni is the number of data points assigned to the centroid, and$\sum {x_j}$ represents the summation of the feature values of all the data points assigned to the centroid.
These steps are repeated iteratively until the centroids stabilize and the clusters converge. The final result is a set of clusters where each data point is assigned to the nearest centroid.
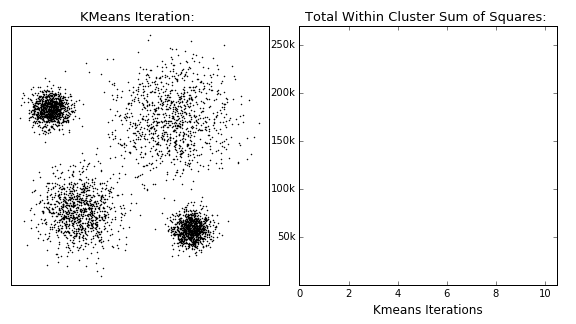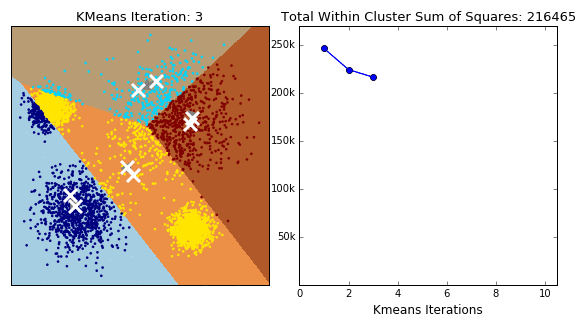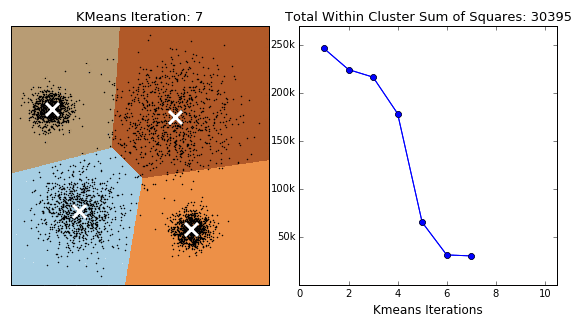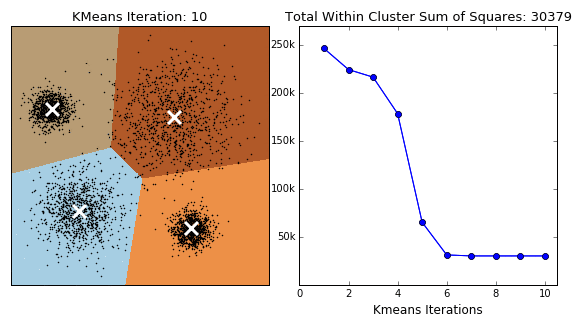
The iris dataset (UCI) was used with the columns as,
- sepal length
- sepal width
- petal length
- petal width
- class (y – dependent variable)
The dataset can be used to classify what the iris plant species is (Iris Setosa, Iris Versicolour, Iris Virginica).