Program to give the multiplication of two NxN matrices using strassen method
Strassens Multiplication follows the method of Divide and Conquer. The idea of Strassen’s method is to reduce the number of recursive calls. Strassen’s method is similar to the regular, simple divide and conquer method in the sense that this method also divide matrices to sub-matrices of size N/2 x N/2 as shown in the above diagram, but in Strassen’s method, the four sub-matrices of result are calculated using following formulae.
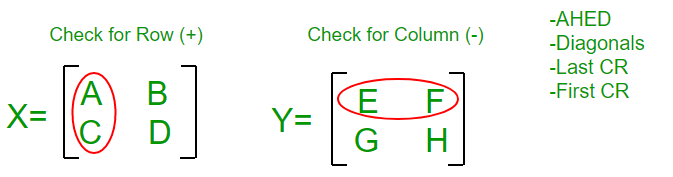
AHED (Learn it as ‘Ahead’) Diagonal Last CR First CR Also, consider X as (Row +) and Y as (Column -) matrix
Write P1 = A; P2 = H; P3 = E; P4 = D For P5 we will use Diagonal Rule i.e. (Sum the Diagonal Elements Of Matrix X ) * (Sum the Diagonal Elements Of Matrix Y ), we get P5 = (A + D)* (E + H)
P1 = A P2= H P3= E P4= D P5= ( A + D ) * ( E + H )
For P6 we will use Last CR Rule i.e. Last Column of X and Last Row of Y and remember that Row+ and Column- so i.e. (B – D) * (G + H), we get P6 = (B – D) * (G + H) For P7 we will use First CR Rule i.e. First Column of X and First Row of Y and remember that Row+ and Column- so i.e. (A – C) * (E + F), we get P6 = (A – C) * (E + F)
P1 = A P2= H P3= E P4= D P5= ( A + D ) * ( E + H ) P6= ( B – D ) * ( G + H) P7= ( A – C ) * ( E + F)
Come Back to P1 : we have A there and it’s adjacent element in Y Matrix is E, since Y is Column Matrix so we select a column in Y such that E won’t come, we find F H Column, so multiply A with (F – H) So, finally P1 = A * (F – H)
P1 = A * ( F – H) P2= H P3= E P4= D P5= ( A + D ) * ( E + H ) P6= ( B – D ) * ( G + H) P7= ( A – C ) * ( E + F)
Come Back to P2 : we have H there and it’s adjacent element in X Matrix is D, since X is Row Matrix so we select a Row in X such that D won’t come, we find A B Column, so multiply H with (A + B) So, finally P2 = H * (A + B) Come Back to P3 : we have E there and it’s adjacent element in X Matrix is A, since X is Row Matrix so we select a Row in X such that A won’t come, we find C D Column, so multiply E with (C + D) So, finally P3 = E * (C + D)
P1= A * ( F – H ) P2= H * ( A + B ) P3= E * ( C + D ) P4= D P5= ( A + D ) * ( E + H ) P6= ( B – D ) * ( G + H) P7= ( A – C ) * ( E + F)
Come Back to P4 : we have D there and it’s adjacent element in Y Matrix is H, since Y is Column Matrix so we select a column in Y such that H won’t come, we find G E Column, so multiply D with (G – E) So, finally P4 = D * (G – E) We are done with P1 – P7 equations, so now we move to C1 – C4 equations in Final Matrix C :
Remember Counting : Write P1 + P2 at C2 Write P3 + P4 at its diagonal Position i.e. at C3 Write P4 + P5 + P6 at 1st position and subtract P2 i.e. C1 = P4 + P5 + P6 – P2 Write odd values at last Position with alternating – and + sign i.e. P1 P3 P5 P7 becomes C4 = P1 – P3 + P5 – P7
Thats all folks!
