The 2006 1D code compiled without edits, and started running & finding eigenmodes! You must set N to be a sensible value (i.e. 1024 pixels) to compile it as the 2D version, otherwise it crashes with a cryptic linker error about truncation.
On a 2017 Mac:
brew install fftw freeglut
make mac
./glFL
If you're on Linux, you should be able to figure it out :^)
It should open a window and start generating eigenmodes, like this rather low-res (hey - it was 2006! I had to run this overnight on my Duron.) YouTube video.
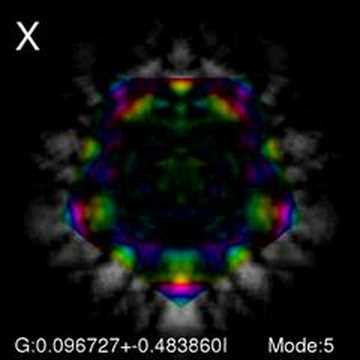
It's simulating the light bouncing around a (highly magnifying) laser cavity. It does this by solving the Huygens-Fresnel integrals in reciprocal space. Practically this means the code spends all its time flipping between real and reciprocal space via Fast Fourier Transforms. The modes form pretty self-similar patterns, when you also have a polygonal aperture in the laser caving.
In the simulation, the brightness is the light intensity, and then the phase information is projected onto a colour sphere.
Codes were written to simulate the propagation of monochromatic light through a bare optical resonator, using a computational Fourier method to solve the Huygens-Fresnel integral. This was used, in the Fox-Li method, to find the lowest-loss eigenmodes of arbitrary cavity designs. An implicit shift ‘hopping’ method was employed to allow a series of increasingly higher-loss eigenmodes to be found, limited in number by computational time.
Codes were confirmed in their accuracy against the literature, and were used to investigate a number of different cavity configurations.
In addition to confirming the fractal nature of eigenmodes imaged at the conjugate plane of a symmetric (g < −1) resonator, an initial study was made of how the (imperfect) quality of the fractal fit varied as the defining aperture was moved around the cavity.
A comparison was also made with the fractal-patterns produced by codes written to simulate basic video-feedback.