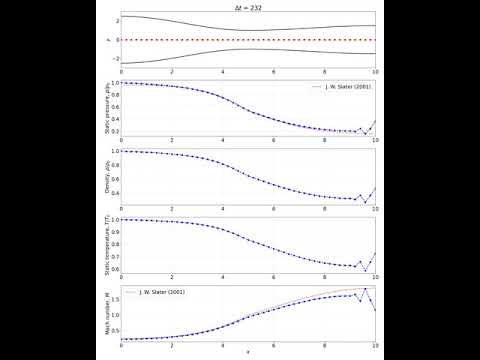
Quasi-1D Subsonic-Supersonic Isentropic Convergent-Divergent Nozzle Flow Simulation with MacCormack's Technique

A flow field solution of a quasi-1D isentropic nozzle was calculated using the time-marching method and MacCormack's discretization scheme. This method is useful for subsonic-supersonic flow field simulation because some popular numerical methods such as the method of characteristics are only applicable to pure supersonic flow fields (governed purely by hyperbolic PDE). The time-marching method whose solution is shown here is not limited by PDE class. The code was validated against J. W. Slater's CFD study on NASA's Converging-Diverging Verification (CDV) model. The tools I used to generate both the solution and the visualization are good ol' numpy and matplotlib. The algorithm is featured in Appendix B of Modern Compressible Flow with Historical Perspective, 4th Edition by John D. Anderson