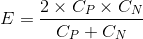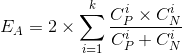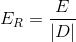Calculate cost-based metrics about binary classification data.
These cost metrics are used at the core of the classification algorithms CSTree, CSForest, BCSForest, and BCF.
Full documentation available here.
The library can be downloaded and installed using pip. Enter this at the terminal (Mac/Linux/Unix) or command prompt (Windows):
pip install datacostAt a Python command line or in a Python script, write this to load the library:
import datacostCost-matrices in datacost are in the format shown in the code block below. They're a dictionary with the keys 'TP', 'TN', 'FP', and 'FN'.
cost_matrix = {'TP':1, 'TN':0, 'FP':1, 'FN':5}A list of available metrics is available further down in this ReadMe. The following example code calculates the expected cost for a dataset with 4 positive records, 10 negative records. It uses the cost_matrix defined in Step 3. It should output approximately 16.47. Try it out!
datacost.expected_cost(4, 10, cost_matrix)- NTN: Number of true negative predictions.
- NTP: Number of true positive predictions.
- NFN: Number of false negative predictions.
- NFP: Number of false positive predictions.
- CTN: Cost incurred by true negative predictions.
- CTP: Cost incurred by true positive predictions.
- CFN: Cost incurred by false negative predictions.
- CFP: Cost incurred by false positive predictions.
The cost incurred by labelling as negative is calculated as:
CN = NTN X CTN + NFN X CFN
The cost incurred by labelling as positive is calculated as:
CP = NTP X CTP + NFP X CFP
The expected cost is typically a representation of how much a set of data points can be expected to cost a business. It is represented by the symbol E. The equation for E is as follows:
After a split, a set of data points has several new sets of class supports, one for each split. The expected cost difference can be calculated as the difference between E for the original dataset, and the summed E over all splits. The equation for expected cost after a split is as follows:
Where k is the number of splits, CPi is the value of CP for the i'th split.
The expected cost per data point is simply the expected cost for a dataset divided by the number of data points in the dataset. It is a way of normalizing expected cost such that logical comparisons may be made between the expected cost of two datasets of different size.
Where |D| is the number of records in the dataset D.
The total cost for a set of records is calculated as either CN or CP, whichever is lowest.
CT = min(CN, CP)