micrograd-tensor is a minimal autograd engine that I build to learn how backpropogation works under the hood in deep learning frameworks. It is based on and extends Karpathy’s micrograd to support tensor operations with NumPy.
At its core is a Tensor class supporting common tensor operations and deep learning functions, with backpropagation via a dynamically constructed DAG. It also includes a small nn library with MLP implementation. The core Tensor and nn combined is just ~240 lines of code (without docs, comments and whitespaces)
- Tensor-based Autograd: Implements a
Tensorobject that wraps a NumPy array, with automatic backpropogation. - Common Operator Support: Supports essential operatioons for building Neural Nets.
- Arithmetic: Addition, multiplication, power, subtraction, division (with broadcasting support).
- Matrix Operations: Matrix multiplication (
@), transpose (.T). - Activation Functions:
ReLU,Sigmoid,Tanh. - Loss Functions:
log_softmaxfor cross-entropy loss. - Other Ops:
sum, indexing.
- Neural Network Module: Includes a simple
MultiLayerPerceptronclass for building feed-forward neural networks.
The notebooks demo-moon.ipynb and demo-mnist.ipynb provides demos on training Neural nets (MLPs) using nn.MultiLayerPerceptron library.
This demo trains a 2 layer neural net with ~340 params on generated moons dataset using SVM's max-margin loss and SGD for optimization. Achieves 100% accuracy.
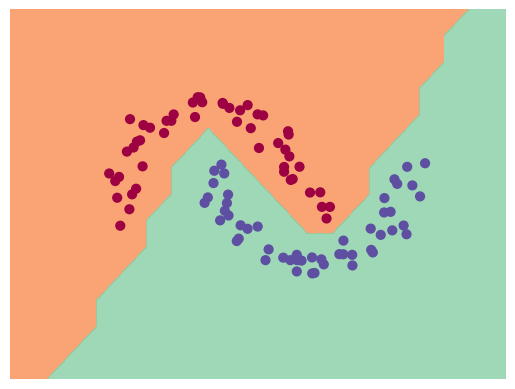
Final decision boundary for the moons dataset
A slight advanced demo that tackles the famous MNIST handwritten digit recognition task. An MLP with two hidden layers with ~11k params. After trained for 20 epochs, Achieves decent 96% accuracy on test set.
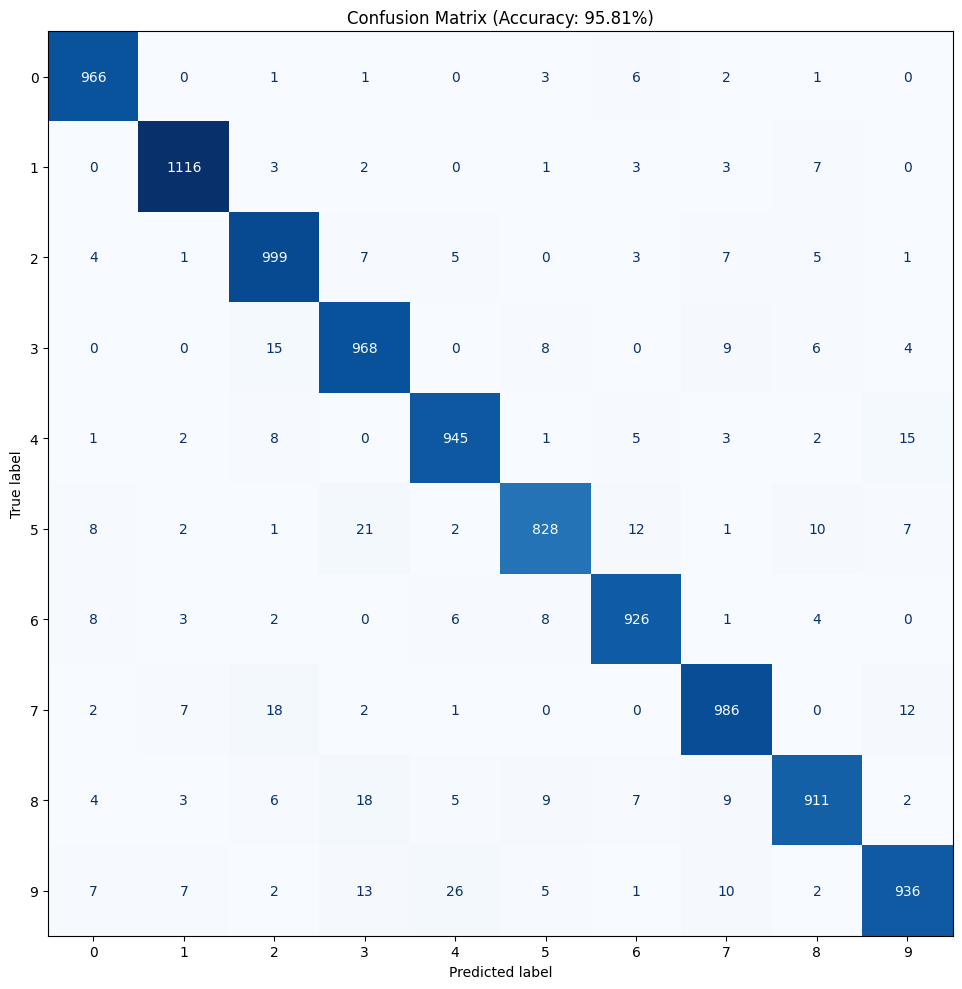
Confusion matrix on the MNIST test set
Below is a arbitrary example showing how to use tensor
from micrograd.engine import Tensor
X_data = np.random.uniform(-1, 1, (16, 16))
W_data = np.random.uniform(-1, 1, (16, 1))
b_data = np.random.uniform(-1, 1, (1))
X_m = Tensor(X_data)
W_m = Tensor(W_data)
b_m = Tensor(b_data)
z_m = (X_m @ W_m) + b_m
z_m.backward()The heart of the library is the Tensor class. Each Tensor instance holds a data value (a NumPy array) and a grad value. When two tensors are combined in an operation (e.g., c = a + b), a new tensor c is created which stores its parent tensors (a and b) as part builing a DAG and a _backward function. This function knows how to compute the gradients of the loss with respect to a and b based on the gradient of the loss with respect to c.
Calling .backward() on a final tensor (e.g., the loss) first builds a topological ordering of the graph. It then iterates through the tensors in reverse order and calls the _backward function for each one, which calculates and accumulates the gradient in the .grad attribute of its parent tensors.
Included a test suite in test.py. These tests compare the results of the operation and the computed gradients with those from PyTorch. To run the tests,
python test.pyMIT
