About GSM | Project Description | Team | Deployment | External Links |
As a trans-national chemical contracting company operating in a complex and ever-changing world, GSM chemical co. is committed to adhering to the highest of global standards of performance ethical corporate conduct.
For more details, please visit GSM.
Appraise | Define Phase | Layout Phase | Presentation |
Bentham Coporation requires the production of 100,000 te y-1 of styrene monomer at purity of 99.7 mol%. (See Project Specification for more details)
Syteren is a monomer used in the production of polymers including polystrene, acrylonitrile butadiene styrene (ABS) and styrene-butadiene (SBR). Following fluctuations in the price of polystyrene the board would like a recommendation on which polymer should be produced from the styrene monomer.
Summary | Process Route Review | Feedstock and Market Review | Material and Energy Balances | Process Block Flow Diagram | Plant Layout |
The aim of this plant design project is to provide critical insights into and recommendations of the available synthetic routes to styrene along with market, feedstock, economic, and sustainability analyses of the venture. This has culminated in a preliminary overview of the plant design and operation in the area of Ordos, China, produced for our clients at Bentham Corporation.
-
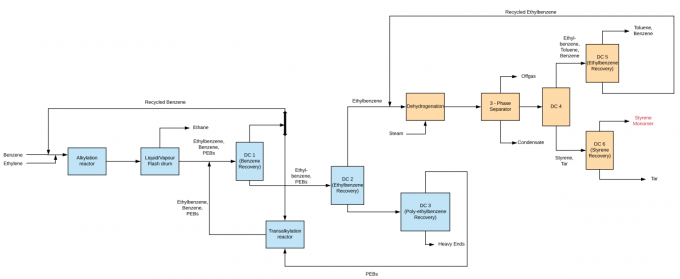
Three Methods for Ethylbenzene Manufacture:
-
Methods for Styrene Manufacture:
-
Dehydrogenation-the dehydrogenation of ethylbenzene to styrene takes -
PO-SM CoproductionCoproduction (Propylene oxide and Styrene monomer):a). Oxidation of ethylbenzene to ethylbenzene hydroperoxide
b). Epoxidation of ethylbenzene hydroperoxide with propylene to form α-phenylethanol and propylene oxide
c). Dehydration of α-phenylethanol to styrene
-
See Process Route Review for more details.
-
Benzene
1. Key component in petrochemical industry global demand 46 million tonnes.
2. 50% used to make ethylbenzene.
3. Not produced directly but as a by-product of other industries - oil refineries, steam cracking of naphthalene, coal used in steel production.
4. North East Asian Market 40% of Benzene market.
5. China is the largest producer and consumer of Benzene.
6. Price of Benzene in China 5,300-5,350 Yuan/te (Q3 2018).
7. Direct routes to obtain benzene now being explored.
8. Converted from other aromatics and dehydro-aromatisation reaction with ethane.
-
Ethylene
1. Ehtylene importance unparalleled in industry/Largest petrochemical by volume in 2018.
2. Wide variety of uses including in surfactants and plasticisers as well as to produce Ethylbenzene.
3. Obtained from distillation of natural gas and oil.
4. Alternative non fossil fuel methods of production.
5. Prices in China 9,978-10,254 Yuan/te (Q2 2014).
-
Styrene
Asia:
Supply rose in most parts of northeast Asia as plants in Japan restarted from turnarounds and South Korean manufacturers were running at higher rates, on better margins in comparison with Q1. Only Taiwan saw a drop in production because of maintenance. Western supply levels were higher on the opened arbitrage window and rising run rates after Q1 maintenance plans. Import demand from China and northeast Asia were both healthy owing to healthy importer margins for most of Q2, and wider downstream production margins especially in the ABS and PS sectors respectively.
Europe:
Europe styrene was oversupplied during the second quarter. Supply was in abundance as demand was sharply reduced as lockdown measures were enforced across the region to control the spread of the coronavirus. A near halt in end-use automotive and tyre manufacturing and consumption destroyed demand for derivative ABS and SBR. Low PO demand resulted in reduced SM/PO output, but supply was still long because of low demand. Europe styrene demand fell sharply in the second quarter, as manufacturing along the supply chain, and end-use consumption were drastically impacted by enforced lockdowns to contain the spread of the coronavirus. The key end-use automotive sector was particularly affected, destroying demand for styrene derivatives such as ABS and SBR. PS and EPS demand was also slow, but packaging and single-use plastic demand picked up slightly.
US:
Supply was tighter in Q2 as US producer AmSty had some equipment issues while restarting its 953,000 tonne/year plant in Saint James, Louisiana, after planned maintenance. Producer INEOS Styrolution began a turnaround in mid-March at its 455,000 tonne/year plant in Texas City, Texas. The company has yet to restart the plant, likely because of demand destruction associated with the pandemic. The tight supply had minimal effect on the market because demand was soft. Overall demand was soft in Q2 as much of the country shut down to prevent the spread of the coronavirus. The North American auto industry shut down in March after an employee at a plant in Michigan contracted the virus. There were some pockets of improved demand related to the pandemic, including for some styrene derivatives such as including ABS for use in ventilators and PS as bans on single-use plastics were eased.
See Feedstock and Market Review for details.
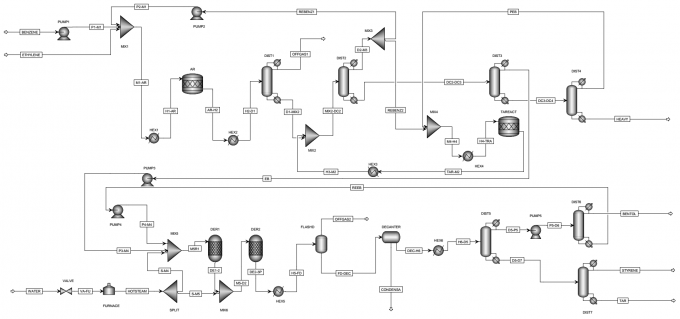
- Material Balances Given that the desired annual production rate of styrene is 100,000 te/year (33.239 mol/s), we can employ back-propagating mehtod to solve material balances for each unit based on certain assumptions.
Table 1. Reaction extents of reactions within dehydrogenation reactor.
| Reaction | Reaction Extent (mol/s) | Selectivy |
|---|---|---|
| 33.239 | 95.514% (Styrene) | |
| 0.800 | 2.299% (Toluene) | |
| 0.4296 | 2.122% (Benzene) | |
| 0.0272 | 0.0785% (Heavy ends) |
Table 2. Reaction extents of reactions within alkylator and transalkylator.
| Reaction | Reaction Extent (mol/s) | Selectivy |
|---|---|---|
| 31.865 | 91.1% (Ethylbenzene) | |
| 2.631 | 8.2% (Diethylbenzene) | |
| 0.225 | 0.7% (Heavy ends) | |
| 2.631 | --- |
- Energy Balances Due to the fact that there is no shaft work, the energy balance in terms of conversion can be written in a simple form as follows:
Table 3. Chemical component information. Note: 888.15K is the mean temperature of dehydrogenator.
| Components | Heat Capacity (kJ/kmolK) at T = 888.15K | Enthalpy of formation (kJ/mol) at ambient temperature | i |
|---|---|---|---|
| Ethlybenzene | 297.242 | 29.92 | 1 |
| Toluene | 247.482 | 50.17 | 0.00127 |
| Styrene | 269.728 | 147.4 | 0 |
| Benzene | 200.787 | 82.88 | 0 |
| Ethylene | 89.4347 | 52.510 | 0 |
| Methane | 67.801 | -74.52 | 0 |
| Hydrogen | 29.815 | 0 | 0 |
| Water | 39.827 | -241.814 | 15.221 |
Table 4. Heat of reaction for three major reactions within dehydrogenation reactor at T = 888.15K (the mean temperature of dehydrogenator).
| Reactions(j=1:3) | |||
|---|---|---|---|
| j=1 | 2.301 | 118.838 | |
| j=2 | 18.041 | -43.626 | |
| j=3 | -7.020 | 101.328 |
The purpose of this report is to find the optimal dimensions and the optimal operating variables of two dehydrogenation reactors. More specifically, the height and diameter, catalyst amount and characteristics, heat exchange strategy of reactors need to be determined optimally. The operating conditions include temperature and pressure as well as the steam-to-ethylbenzene ratio.
- Install Wolfram Mathematica ( Version 11.0 or higher) or Wolfram Cloud (App or Online Version);
- Running codes within the software interface, e.g., you can run the following codes to get concentration profiles for reactor 1:
Manipulate[Module{(At1, At2, At3, Et1, Et2, Et3, kt1, kt2, kt3, k1, k2, k3, k4, A1, A2, A3, A4, E1, E2,
E3, E4, AEB, AST,AH2, ΔHaEB, ΔHaST, ΔHaH2, KEB, KST, KH2, rt1, rt2, rt3, rc1, rc2, rc3, rc4, Keq, FEB0,
FST0,BZ0, FTO0, FH20, FCH40, FC2H40, FH2O0, FT0, PEB, PST, PBZ, PETH, PTO, PH2, PCH4, PC2H4, PH2O, PMTH,
C1EB, C1ST, C1BZ, C1ETH, C1TO, C1H2, C1MTH, C1H2O, S1ST, S1BZ, S1TO, S1H2, ΔH1, ΔH2, ΔH3, ΔH4, Cp1, Cp2,
Cp3, Cp4, Cp5, Cp6, L, Di, Ac, dp, μ, u, G, ρb, R, ϵ, ρg},
(*Model Construction of The Thermal Reactions*)
At1 = 2.2215 * 10^16; (**kmol/m3hbar**)
At2 = 2.4217 * 10^20;
At3 = 3.8224 * 10^17;
Et1 = 272.23; (**kJ/mol**)
Et2 = 352.79;
Et3 = 313.06;
R = 8.314;
kt1 = At1 * Exp[(-Et1 * 10^3)/(R * T[z])]; (**kmol/m3hbar**)
kt2 = At2 * Exp[(-Et2 * 10^3)/(R * T[z])];
kt3 = At3 * Exp[(-Et3 * 10^3)/(R * T[z])];
(*Thermal Reaction Rates of Three Reactions*)
rt1 = kt1 * (PEB - (PST * PH2)/Keq); (**kmol/m3h**)
rt2 = kt2 * PEB;
rt3 = kt3 * PEB;
(*Model Construction of The Catalytic Reactions*)
A1 = 4.594 * 10^9; (**kmol/kg-cath**)
A2 = 1.060 * 10^15;
A3 = 1.246 * 10^26;
A4 = 8.024 * 10^10;
E1 = 175.38; (**kJ/mol**)
E2 = 296.29;
E3 = 474.76;
E4 = 213.78;
k1 = A1* Exp[(-E1 * 10^3)/(R * T[z])]; (**kmol/kg-cath**)
k2 = A2* Exp[(-E2 * 10^3)/(R * T[z])];
k3 = A3* Exp[(-E3 * 10^3)/(R * T[z])];
k4 = A4* Exp[(-E4 * 10^3)/(R * T[z])];
(*Catalytic Reaction Rates of Four Reactions*)
rc1 = (k1 * KEB * (PEB - (PST*PH2)/Keq))/(1 + KEB * PEB + KH2 * PH2 + KST * PST)^2;(**kmol/kg-cath**)
rc2 = (k2 * KEB * PEB)/(1 + KEB * PEB + KH2 * PH2 + KST * PST)^2;
rc3 = (k3 * KEB * PEB * KH2 * PH2)/(1 + KEB * PEB + KH2 * PH2 + KST * PST)^2;
rc4 = (k4 * KST * PST * KH2 * PH2)/(1 + KEB * PEB + KH2 * PH2 + KST * PST)^2
(*Model Construction for The Thermodynamic Equilibriums*)
AEB = 1.014 * 10^-5; (**1/bar**)
AST = 2.678 * 10^-5;
AH2 = 4.519 * 10^-7;
ΔHaEB = -102.22; (**kJ/mol**)
ΔHaST = -104.56;
ΔHaH2 = -117.95;
KEB = AEB * Exp[(-ΔHaEB * 10^3)/(R * T[z])]; (**1/bar**)
KST = AST * Exp[(-ΔHaST * 10^3)/(R * T[z])];
KH2 = AH2 * Exp[(-ΔHaH2 * 10^3)/(R * T[z])];
Keq = Exp[-(122725.157 - 126.267 * T[z] - 0.002194 * T[z] * T[z])/(R * T[z])];(**1/bar**)
(*The Initial Molar Flowrates of Components*)
FEB0 = 49.7976 * 3600/ 1000; (**kmol/h**)
FST0 = 0.00332919 * 3.6;
FBZ0 = 1.464 * 3.6;
FTO0 = 0.0482245 * 3.6;
FH20 = 0;
FCH40 = 0;
FC2H40 = 0;
FH2O0 = 1080 * 3.6;
FT0 = FEB0 + FST0 + FBZ0 + FTO0 + FH20 + FCH40 + FC2H40 + FH2O0;
(*Partial Pressure of Components*)
PEB = PT[z] * (FEB0/FT0)(1 - (X1EB[z] - X1BZ[z] - X1TO[z]) - X1BZ[z] - X1TO[z])/(1 + FEB0/FT0 * (X1TO[z] + X1BZ[z] + X1H2[z]));
(**1/bar**)
PST = PT[z] * (FST0/FT0 + FEB0/FT0 * (X1EB[z] - X1BZ[z] - X1TO[z])/(1 + FEB0/FT0 *(X1TO[z] + X1BZ[z] + X1H2[z]))^2;
PBZ = PT[z] * (FBZ0/FT0 + FEB0/FT0 * X1BZ[z])/(1 + FEB0/FT0 * (X1TO[z] + X1BZ[z] + X1H2[z]));
PH2 = PT[z] * (FH20/FT0 + FEB0/FT0 * X1H2[z])/(1 + FEB0/FT0 * (X1TO[z] + X1BZ[z] + X1H2[z]));
PETH = PT[z] * (FC2H40/FT0 + FEB0/ FT0 * X1BZ[z])/( 1 + FEB0/FT0 * (X1TO[z] + X1BZ[z] + X1H2[z]));
PTO = PT[z] * (FTO0/FT0 + FEB0/FT0 * X1TO[z])/(1 + FEB0/FT0 * (X1TO[z] + X1BZ[z] + X1H2[z]));
PH2O = PT[z] * (FH2O0/FT0)/(1 + FEB0/FT0 * (X1TO[z] + X1BZ[z] + X1H2[z]));
PMTH = PT[z] * (FCH40/FT0 + FEB0/FT0 * X1EB[z])/( 1 + FEB0/FT0 * (X1TO[z] + X1BZ[z] + X1H2[z]));
(*Concentration of Components*)
C1EB = PEB * 10^5 / (R * T[z]);
C1ST = PST * 10^5 /(R * T[z]);
C1BZ = PBZ * 10^5/(R * T[z]);
C1H2 = PH2 * 10^5/(R * T[z]);
C1ETH = PETH * 10^5/(R * T[z]);
C1TO = PTO * 10^5/(R * T[z]);
C1H2O = PH2O * 10^5/(R * T[z]);
C1MTH = PMTH * 10^5/(R * T[z]);
(*Selectivity of Reaction Products*)
S1ST = (X1EB[z] - X1BZ[z] - X1TO[z])/X1EB[z];
S1BZ = X1BZ[z]/X1EB[z];
S1TO = X1TO[z]/X1EB[z];
S1H2 = X1H2[z]/X1EB[z];
(*Heat of reactions*)
ΔH1 = 117690 + 41.99 * (T[z] - 298.15) + (-8.2026 * 10^-2)/2 * ((T[z])^2 - 298.152^2 +(6.499 * 10^-5/3)*((T[z])^3 - 298.153^3
+ (-2.311 * 10^-8)/4 * ((T[z])^4 - 298.154^4); (**kJ/kmol**)
ΔH2 = 105510 + 12.986 * (T[z] - 298.15) + (-7.67 * 10^-2)/2 * ((T[z])2 - 298.152^2 + (9.592 * 10^-5)/3 * ((T[z])^3 - 298.153^3
+ (-4.125 * 10^-8)/4 * (T[z])^4 - 298.154^4);
ΔH3 = -54680 + 10.86 * (T[z] - 298.15) + (-15.1844* 10^-2)/2 * ((T[z])^2 - 298.152^2) + (23.04 * 10^-5/3)((T[z])^3 - 298.153^3)
+ (-9.9955 * 10^-8)/4*((T[z])^4 - 298.154^4));
ΔH4 = -172370 + (-31.13) * (T[z] - 298.15) + (-6.9818* 10^-2)/2 * ((T[z])^2 - 298.152^2 + (16.54 * 10^-5)/3*((T[z])^3 - 298.153^3)
+ (-7.685 * 10^-8)/4 * ((T[z])^4 - 298.154^4);
(*Heat Capacities of Components*)
Cp1 = -0.43426 + 6.0671 * 10^-3 * T[z] - 3.8625 * 10^-6 * T[z] * T[z] + 9.1282 * 10^-10 * (T[z])^3; (*kJ/kgK*)
Cp2 = -0.26436 + 5.564 * 10^-3 * T[z] - 3.0018* 10^-6 * T[z] * T[z] + 5.3317 * 10^-10 * (T[z])^3;
Cp3 = -0.40599 + 6.6616 * 10^-3 * T[z] - 4.5318* 10^-6 * T[z] * T[z] + 12.255 * 10^-10 * (T[z])^3;
Cp4 = -0.27127 + 5.9142* 10^-3 * T[z] - 3.8631 * 10^-6 * T[z] * T[z] + 9.54 * 10^-10 * (T[z])^3;
Cp5 = 13.57 + 4.637 * 10^-3 * T[z] - 6.905 * 10^-6 * T[z] * T[z] + 38.23 * 10^-10 * (T[z])^3;
Cp6 = 1.7911 + 0.1069* 10^-3 * T[z] + 0.58611* 10^-6 * T[z] * T[z] - 1.998 * 10^-10 * (T[z])^3;
(*Physical properties of the catalyst*)
dp = 5.5 / 1000; (**m**)
ρb = 1422;
ϵ = 0.4312;
(*Dimensions of the reactor*)
L = 10;
Di = Dr/100;
Ac = π/4 * (Di)^2;
(*The important properties of the gas mixture*)
μ = (-10.035 + 0.25191 * T[z] - 0.000037932 * T[z] * T[z]) * 3.6 * 10^-4; (*kg/ms*)
u = 22.003/Ac;
G = 89520.109/Ac;
ρg = (10^5 * 10^-3)/(R * T[z]) * (PEB * 106.168 + PST * 104.15 + PBZ * 78.114 + PTO * 92.141 + PH2O * 18.020 + PH2 * 2.010
+ PMTH * 16.043 + PETH * 28.054);
r101 = Quiet @ NDSolve[{X1EB'[z] ⩵ (rc1 + rc2 + rc3 + (rt1 + rt2 + rt3) * ϵ/ρb) * (Ac* ρb)/FEB0, X1BZ'[z] ⩵ (rc2 + rt2 * ϵ/ρb)
* (Ac* ρb)/FEB0, X1TO'[z] ⩵ (rc3 + rc4 + rt3 * ϵ/ρb) * (Ac* ρb)/FEB0, X1H2'[z] ⩵ (rc1 - rc3 - 2 rc4 + (rt1 - rt3) * ϵ/ρb)* Ac
* ρb/FEB0, PT'[z] ⩵ -(1 - ϵ)/ϵ3 *(1.28 + 458* (1 - ϵ)/(ρg * dp * u/μ) * 7.7160 * 10^-8 * u * G * FEB0/(ρb* dp * Ac) * 10-5 * Ac
* ρb/FEB0, T'[z] == Ac* ρb/FEB0 * (1 / (106.168* FEB0 * (1 - X1EB[z]) * Cp1 + 104.15 * (FST0 + FEB0 * (X1EB[z] - X1BZ[z] -
X1TO[z])) * Cp2 + 78.114 * (FBZ0 + FEB0 * X1BZ[z]) * Cp3 + 92.141 * (FTO0 + FEB0 * X1TO[z]) * Cp4 + 2.010 * (FH20 + FEB0 *
X1H2[z]) * Cp5 + 18.020* FH2O0 * Cp6)) * (FEB0 * (-ΔH1 * (rc1 + rt1 * ϵ/ρb) - ΔH2 * (rc2 + rt2 * ϵ/ρb) - ΔH3 *(rc3 + rt3 * ϵ/ρb)
- ΔH4 * rc4)), X1EB[0] ⩵ 0, X1BZ[0] ⩵ 0, X1TO[0] ⩵ 0, X1H2[0] ⩵ 0, PT[0] ⩵ 1.25, T[0] ⩵ 886}, {PT, T, X1EB, X1BZ, X1TO,
X1H2, C1EB, C1ST, C1BZ, C1TO, C1H2, C1ETH, C1H2O, C1MTH}, {z, 0, 2}];
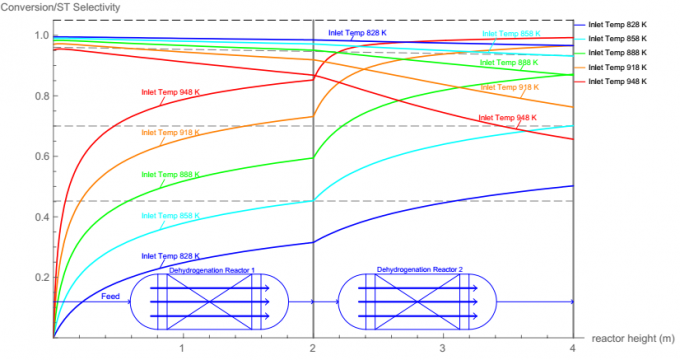
Figure1 = Plot[{C1EB /. r101, C1ST /. r101, C1BZ /. r101, C1TO /. r101, C1H2 /. r101, C1ETH /. r101, C1MTH /. r101}, {z, 0, 2},
PlotRange→ All, AxesLabel → {"Reactor height (m)", "Concentration (mol/cum)"}, PlotLegends → {"EB", "ST", "BZ", "TO", "H2",
"ETH", "MTH"}, PlotLabels → Placed[{"EB", "ST", "BZ", "TO"}, Above]]], Column[{Control[{{Dr, 400, "reactor diameter (cm)"}}, 100,
800, 10, Appearance → "Labeled"}]}, Left]]- And to get an overview of how temperature, pressure, steam to ethylbenzene ratio on the ethylbenzene conversion, run these codes:
Manipulate[
K[T_] := Exp[A1 + B1 / T + C1 Log[T] + D1 T];
A1 = -13.2117277;
B1 = -13122.4699;
C1 = 4.353627619;
D1 = -0.00329709;
F0 = 152.2;
Fsteam = ratio F0;
Conv[T_] := 1/(2 F0 (P + K[T]))*(-K[T] Fsteam + Sqrt[(K[T] Fsteam) ^ 2 + 4 F0 (P + K[T]) K[T] (F0 + Fsteam)]);
Conv1[T_] := 1/(2 F0 (P + K[T]))* (Sqrt[4 F0 (P + K[T]) K[T] (F0)]);
Show[Plot[Conv1[T], {T, 500, 1500}, Frame → True, FrameLabel → {"temperature", "conversion"}, AxesOrigin→ {500, 0},
PlotLabels → {Callout["Without steam", {Scaled[0.25], Right}]}, PlotStyle → {Thick, Green}], Plot[Conv[T], {T, 500, 1500},
Frame → True, FrameLabel → {"temperature", "conversion"}, PlotLabels → {Callout["With steam", {Scaled[0.25], Left}]},
AxesOrigin→ {500, 0}, PlotStyle → {Thick, Red}], ImageSize → {500, 350}], {{P, 1.37, "total pressure in bar"}},
1, 1.7, 0.01, Appearance → "Labeled"}, {{ratio, 10, "steam to EB flow rate ratio"}}, 0, 20, 0.5, Appearance → "Labeled"}, TrackedSymbols⧴ {ratio, P}]See Wolfram Mathematica Define Phase Code for more details.
This study is to predict safe separation distances via accident consequence modelling of various accidental failure scenarios for hazardous units relevant with ethylene gas dispersion, so as to modify the plant layout accordingly to guarantee safety of personnel in on-site buildings and reduce risks to acceptable level for the population outside the plant, and prevent, limit and mitigate domino effects as much as possible.
This project is part of Advanced Design Project and is developed by an international student team. The maintenance service is assisted by Wei MEI.
This project team members are listed in alphabetical order, with affiliation, and main areas of contribution:
- Alastair Dixon (LinkedIn Profile Alastair Dixon)
- Alex Kearns (LinkedIn Profile Alex Kearns)
- Dusita De Hoop (LinkedIn Profile Dusita De Hoop)
- Dhrupal Godhaniya (LinkedIn Profile Dhrupal Godhaniya)
- Ernest Chu (LinkedIn Profile Ernest Chu)
- Wei MEI (LinkedIn Profile Wei MEI)
This project is done with great help from two Personal Tutors and Prof. Haroun Mahgerefteh:
- Richard Porter (Personal Profile Richard Porter), Module Coordinator, Senior Research Associate and Teaching Fellow at Department of Chemical Engineering, University College London.
- Martynov Sergey (Personal Profile Martynov Sergey), Bentham Corporation Representative, Research Assoicate at University College London.
- Haroun Mahgerefteh (Personal Profile Haroun Mahgerefteh), Bentham Corporation Representative, Professor of Chemical Engineering, University College London.
For more details, please visit this website on Google Drive