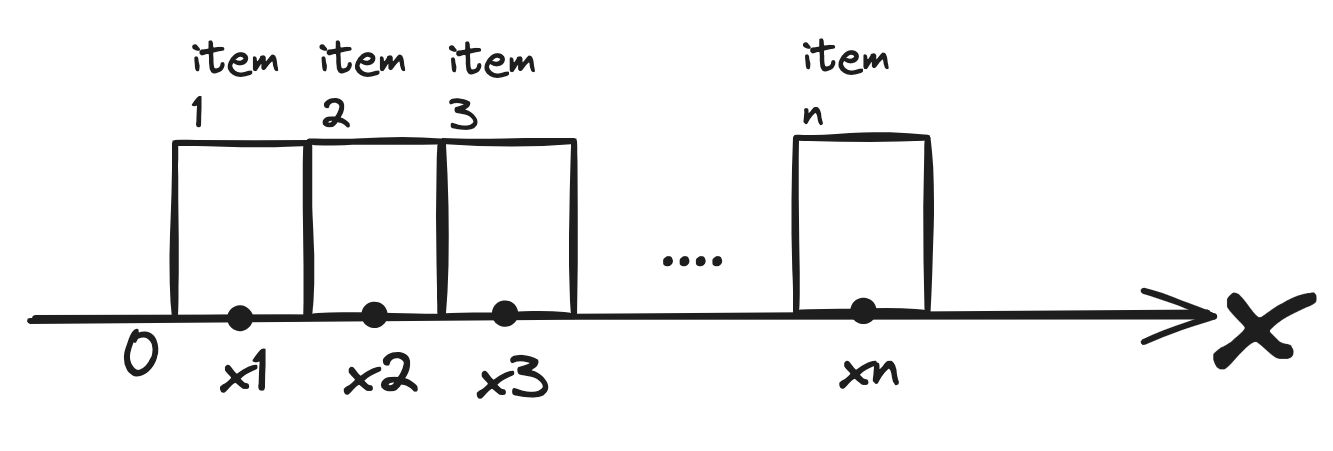
Finding the best location for some items in an aisle in an warehouses. In this warehouse aisle, we are storing a number of items that are to be picked up and shipped to customers.
We want to place the items such that we minimise the distance that the warehouse staff need to move when picking the orders. This maximises the overall efficiency of the warehouse.
we also have a list of representative orders.
Figure out in what sequence to put the items in this aisle, and where the items should be placed relative to the door. (identifying relative x-coordinate of each item w.r.t the door)
The objective is to minimize the total distance that staff needs to move to pick up the items.
Assumption:
- Only one aisle in the whole warehouse.
- The coworkers that pick up the items start by entering through the door, and they finish by exiting through the same door.
- Given the sequence of items, they are placed as closely as possible, with respect to their respective widths.
- The door is located somewhere inside the aisle. You can e.g. imagine that the aisle runs from west to east and the door is located in the north wall. The x-coordinate indicates how far east the door is placed, relative to the middle of the first item (which is assumed to be at
x=0). Larger x-values mean that the door is placed further to the east. - Items are going to be picked in the sequence given by the order. Sequence can be changed for optimizing purpose
- There is an unlimited amount of items available to be picked in each of the item locations
In the file data.json contains:
- For every item to be placed, the width it occupies in the aisle
- A list of items
- A list of orders, where each order is a list of articles to be picked up
where:
-
$X_{i}$ : X-coordinate of item$i$ .
-
$X_0$ : Door offset
-
$m$ : Total order (in this case study$m = 50$ )
-
$n$ : Article list per order
where:
-
$w_{i}, w_{j}$ : width of item$i$ $\neq$ $j$ .
-
$W$ : Total width of all 14 items
-
$min(w_{i})$ : Smallest width value
Since the result is absolute coordinate, and we want the first item to be at 0. So the output needs to substract the minimal absolute coordinates. Items x-coordinate is:
- 'Malm': 0.0
- 'Dvala': 2.98
- 'Ribba': 3.5
- 'Lack': 4.25
- 'Ektorp': 7.1
- 'Billy' and door_offset: 10.9
- 'Fargrik': 12.55
- 'Klippan': 14.3
- 'Stockholm': 17.15
- 'Poang': 18.85
- 'Frakta': 19.6
- 'Docksta': 21.15
- 'Kallax': 23.3
- 'Raskog': 24.75
--> Total optimized distance = 1754.1
Improvement. The above result is assumed the sequence per order is fixed. But we can actually permute the sequence to optimize the walking distance for each order (>= 2 item in sequence). This can be done at following simple pseudo algorithm:
FUNCTION NextItem
Helper Recursive function to find the next nearest item of the given item
FOR each order
IF order has at least 2 items THEN
COMPUTE default distance of sequence
FOR item on sequenceSET item first in the sequence
CALL NextItem
COMPUTE Distance of sequence
REPLACE default sequence by sequence with minimal distance
order sequence is changed at {1, 2, 5, 6, 9, 10, 12, 21, 22, 26, 27, 29, 32, 34, 37, 38, 45, 46, 48, 50}
- 1th order: From ['Stockholm', 'Dvala', 'Poang', 'Malm'] --> ['Dvala', 'Malm', 'Stockholm', 'Poang']
- 2th order: From ['Poang', 'Docksta', 'Dvala', 'Ribba', 'Billy', 'Fargrik'] --> ['Dvala', 'Ribba', 'Billy', 'Fargrik', 'Poang', 'Docksta']
- 5th order: From ['Fargrik', 'Ektorp', 'Frakta', 'Docksta'] --> ['Ektorp', 'Fargrik', 'Frakta', 'Docksta']
- 6th order: From ['Frakta', 'Fargrik', 'Poang', 'Raskog', 'Malm'] --> ['Fargrik', 'Poang', 'Frakta', 'Raskog', 'Malm']
- 9th order: From ['Docksta', 'Frakta', 'Klippan', 'Poang', 'Kallax', 'Dvala'] --> ['Dvala', 'Klippan', 'Poang', 'Frakta', 'Docksta', 'Kallax']
- 10th order: From ['Dvala', 'Billy', 'Kallax', 'Lack', 'Ektorp'] --> ['Dvala', 'Lack', 'Ektorp', 'Billy', 'Kallax']
- 12th order: From ['Stockholm', 'Poang', 'Dvala', 'Kallax', 'Lack', 'Ribba'] --> ['Dvala', 'Ribba', 'Lack', 'Stockholm', 'Poang', 'Kallax']
- 21th order: From ['Poang', 'Ektorp', 'Dvala', 'Malm', 'Klippan', 'Stockholm'] --> ['Ektorp', 'Dvala', 'Malm', 'Klippan', 'Stockholm', 'Poang']
- 22th order: From ['Stockholm', 'Ektorp', 'Dvala', 'Billy', 'Fargrik'] --> ['Dvala', 'Ektorp', 'Billy', 'Fargrik', 'Stockholm']
- 26th order: From ['Klippan', 'Billy', 'Ribba', 'Kallax', 'Frakta', 'Ektorp'] --> ['Ribba', 'Ektorp', 'Billy', 'Klippan', 'Frakta', 'Kallax']
- 27th order: From ['Stockholm', 'Fargrik', 'Raskog', 'Billy', 'Dvala', 'Poang'] --> ['Stockholm', 'Poang', 'Raskog', 'Fargrik', 'Billy', 'Dvala']
- 29th order: From ['Fargrik', 'Ektorp', 'Billy', 'Lack', 'Klippan'] --> ['Ektorp', 'Lack', 'Billy', 'Fargrik', 'Klippan']
- 32th order: From ['Stockholm', 'Klippan', 'Billy', 'Kallax', 'Raskog'] --> ['Klippan', 'Stockholm', 'Kallax', 'Raskog', 'Billy']
- 34th order: From ['Lack', 'Ektorp', 'Billy', 'Malm'] --> ['Malm', 'Lack', 'Ektorp', 'Billy']
- 37th order: From ['Dvala', 'Docksta', 'Lack', 'Stockholm', 'Ektorp'] --> ['Dvala', 'Lack', 'Ektorp', 'Stockholm', 'Docksta']
- 38th order: From ['Malm', 'Fargrik', 'Docksta', 'Billy', 'Kallax'] --> ['Malm', 'Billy', 'Fargrik', 'Docksta', 'Kallax']
- 45th order: From ['Ektorp', 'Poang', 'Ribba', 'Docksta', 'Klippan'] --> ['Ektorp', 'Ribba', 'Klippan', 'Poang', 'Docksta']
- 46th order: From ['Fargrik', 'Billy', 'Raskog', 'Frakta', 'Docksta', 'Kallax'] --> ['Billy', 'Fargrik', 'Frakta', 'Docksta', 'Kallax', 'Raskog']
- 48th order: From ['Lack', 'Poang', 'Ektorp', 'Klippan', 'Billy'] --> ['Lack', 'Ektorp', 'Billy', 'Klippan', 'Poang']
- 50th order: From ['Poang', 'Frakta', 'Kallax', 'Malm', 'Stockholm'] --> ['Malm', 'Stockholm', 'Poang', 'Frakta', 'Kallax']