update

README.md

@@ -1,47 +1,53 @@
 ### ELA
-ELA 全称：Error Level Analysis ，汉译为“错误级别分析”或者叫“误差分析”。通过检测特定压缩比率重新绘制图像后造成的误差分布，可用于识别JPEG图像的压缩。
-[维基百科](https://en.wikipedia.org/wiki/Error_level_analysis)：ELA是对JPEG有损压缩的数字数据中的压缩影像进行分析。
-这个领域的专家非 [Neal Krawetz先生](http://www.hackerfactor.com/) 莫属，其在 [其07年论文](https://www.wired.com/images_blogs/threatlevel/files/bh-usa-07-krawetz.pdf) 中详细的介绍了这项技术的实现。
+ELA 全称：Error Level Analysis ，汉译为“错误级别分析”或者叫“误差分析”。通过检测特定压缩比率重新绘制图片后造成的误差分布，可用于识别JPEG图片的压缩。
+[维基百科](https://en.wikipedia.org/wiki/Error_level_analysis)：ELA是对JPEG有损压缩的数字数据中的压缩影片进行分析。
+ELA技术可参考 [Neal Krawetz先生](http://www.hackerfactor.com/) 在其 [07年论文](https://www.wired.com/images_blogs/threatlevel/files/bh-usa-07-krawetz.pdf) 中的详细介绍。
 
 ### 原理
-正常情况下做有损压缩的图像会均匀地应用于一组数据，导致压缩伪像的均匀水平。
-错误级别分析显示了整个图像的不同错误级别，强烈建议某种形式的数字操纵。
-错误级别分析（ELA）通过以已知错误率（例如95％）故意重新绘制图像，然后计算图像之间的差异来工作。如果几乎没有变化，那么在该质量水平下，单元格已达到其局部最小值误差。然而，如果存在大量的变化，则像素不在其本地最小值处，并且是有效的。
-### 示例
-1. [http://www.errorlevelanalysis.com](http://www.errorlevelanalysis.com) 是专门做ELA分析的网站，可惜现在已经关闭了。但还是保留了一个示例作为参考(请留意嘴唇、衬衫以及眼睛，这些部分与其周围因素是有所不同的，根据推测是经过修改的，区域变亮)：
-![](http://images.43px.com/576ff2a.jpg)
-![](http://images.43px.com/576ff2a_enhanced.jpg)
-2. [Jonas Wagner](https://29a.ch) 个人的测试(可以看到假的部分图像明显高亮于其周围区域)：
-![](http://images.43px.com/fake_screenshot.jpg)
-![](http://images.43px.com/original_screenshot.jpg)
-### 局限性
 
-有了这个说法，算法并不是完全可靠的，尤其是那些经过重新缩放和经常压缩的图像
+把图片分割成很多8x8个正方形中的1像素点，对每一个小块进行单独的色彩空间转换。每次对 JPG 图片的修改，都会进行第二次转换。两次转换自然会存在差异，ELA 就是靠对比这种差异来判断图片的哪部分被修改过。
 
--------
+* 点，指画面中的重复纹理或者类似数据，重复纹理在ELA分析的时候应该表现出近似的颜色，细节较多的区域数据差异也应该大。
+* 线，是不同颜色大面之间的交界线，相同反差边缘应该表现出近似的ELA结果。反差越大，ELA值越高，线条越清晰。
+* 面，纯色面不存在差异，也就不存在ELA，黑色或黑色着色。
 
-更新中。。。
-
--------
+如果非JPEG图片包含可见的网格线（8×8个正方形中的1像素点），则表示图片由JPEG格式转换为非JPEG格式（例如PNG）。
+如果图片是原始PNG，则ELA是边缘和纹理生成非常高的值。如果ELA沿边缘和纹理产生弱结果（黑色或黑色着色），则PNG可能是由JPEG转化而来的。
+### 示例
+1. [http://www.errorlevelanalysis.com](http://www.errorlevelanalysis.com) 是专门做ELA分析的网站，可惜现在已经关闭了。但还是保留了一个示例作为参考(请留意嘴唇、衬衫以及眼睛，这些部分与其周围因素是有所不同的，根据推测是经过修改的，区域变亮)：
+![](http://www.errorlevelanalysis.com/576ff2a.jpg)
+![](http://www.errorlevelanalysis.com/576ff2a_enhanced.jpg)
+2. [Jonas Wagner](https://29a.ch) 的测试(可以看到假的部分图片明显高亮于其周围区域)：
+![](https://29a.ch/sandbox/2012/imageerrorlevelanalysis/fake_screenshot.jpg)
+![](https://29a.ch/sandbox/2012/imageerrorlevelanalysis/original_screenshot.jpg)
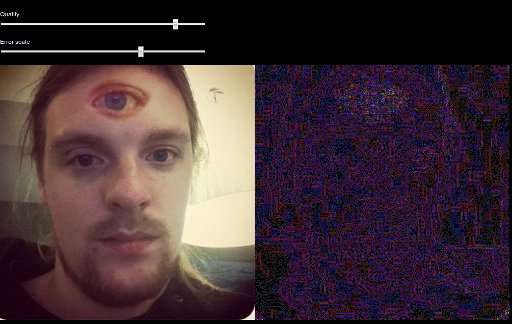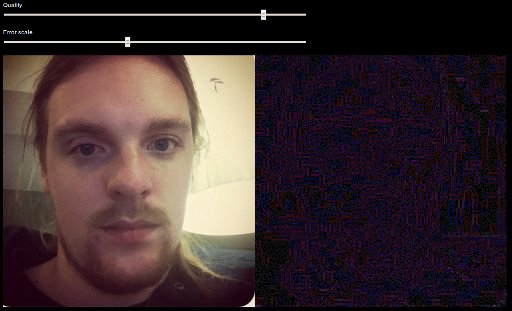+3. 原始照片在重新保存期间具有高度的变化（高ELA值）。后续的任何操作都将降低ELA值，产生较暗的ELA结果：
+
+原图![](http://fotoforensic.com/img/books-orig.jpg)
+原ELA![](http://fotoforensic.com/img/books-orig-ela.png)
+重新保存一次：
+二次保存图![](http://fotoforensic.com/img/books-resave.jpg)
+二次保存后ELA![](http://fotoforensic.com/img/books-resave-ela.png)
+修改图片内容(复制了绿皮书及放置了恐龙玩具)：
+修改后图片![](http://fotoforensic.com/img/books-edited.jpg)
+修改后ELA![](http://fotoforensic.com/img/books-edited-ela.png)
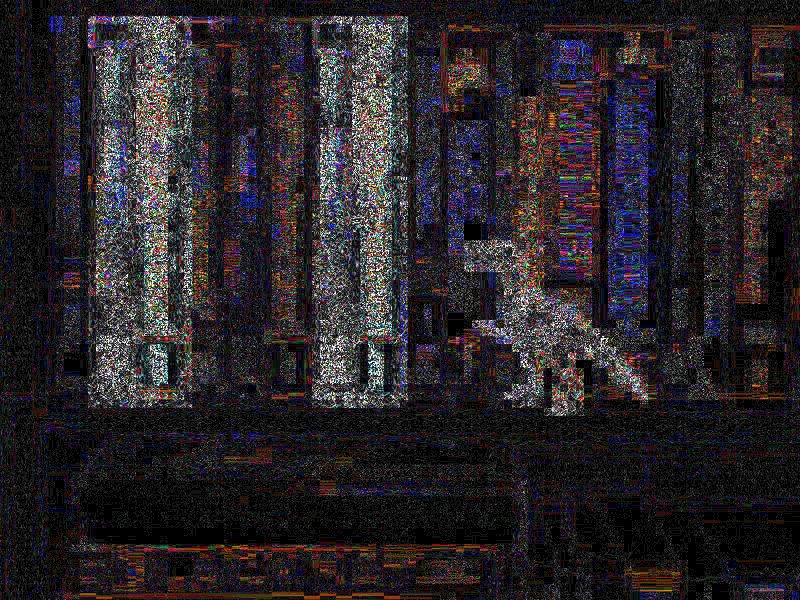+### 局限性
+* ELA只是一种算法，由于其分析压缩的性质，无损压缩的数据（如PNG图片）及图片色彩减少到256色以下(转换为GIF图)，ELA 是没有作用的。
+* 如果图片被重新保存多次，那么它可能完全处于最小错误级。在这种情况下，ELA将显示黑色图片，且不能使用该算法来识别修改。
+目前这个算法并不是完全可靠的，尤其是经过多次压缩的图片。
 
 ###拓展
-
  [Neal Krawetz先生](http://www.hackerfactor.com/) 的 [演讲文档](https://www.wired.com/images_blogs/threatlevel/files/bh-usa-07-krawetz.pdf) 
-[https://29a.ch/](https://29a.ch/) 也有其他关于图像处理的技术，比如：
-自动化图像裁剪主题区域(非暴力裁剪中心区域)的 smartcrop.js [介绍页](https://29a.ch/2014/04/03/smartcrop-content-aware-image-cropping) | [示例页](https://29a.ch/sandbox/2014/smartcrop/examples/testsuite.html) | [测试页]() | [GitHub](https://github.com/jwagner/smartcrop.js/)
+[https://29a.ch/](https://29a.ch/) 也有其他关于图片处理的技术，比如：
+自动化图片裁剪主题区域(非暴力裁剪中心区域)的 smartcrop.js [介绍页](https://29a.ch/2014/04/03/smartcrop-content-aware-image-cropping) | [示例页](https://29a.ch/sandbox/2014/smartcrop/examples/testsuite.html) | [测试页]() | [GitHub](https://github.com/jwagner/smartcrop.js/)
 图片滤镜 Film Emulator
 [测试页](https://29a.ch/film-emulator/) | [GitHub](https://github.com/jwagner/analog-film-emulator)
 
--------
 ```
 参考资料：
 · http://www.hackerfactor.com/
 · http://www.wired.com/images_blogs/threatlevel/files/bh-usa-07-krawetz.pdf
 · http://www.errorlevelanalysis.com/
+· http://fotoforensic.com/tutorial-ela.php
 · https://29a.ch/
-· http://fotoforensic.com/
 · https://en.wikipedia.org/wiki/Error_level_analysis
 ```
--------
-
-