---

📚 DS-BigO-Complexity

📝 Introduction

DS-BigO-Complexity is a comprehensive guide to understanding Data Structures, Algorithms, and Time Complexity. This repository is designed for beginners and intermediate learners who want to strengthen their problem-solving skills and optimize their code for efficiency.

🔹 Learn about common data structures like arrays, linked lists, trees, graphs, and heaps.
🔹 Implement and analyze sorting and searching algorithms.
🔹 Master Big-O Notation and understand time & space complexity.
🔹 Solve real-world coding problems with optimized solutions.

---

🚀 Features

• In-depth explanations of fundamental data structures
• Hands-on implementations in Python
• Big-O Complexity Analysis for each algorithm
• Visual representations of sorting & searching algorithms
• Interview-style problems with optimal solutions
• Practice problems & challenges

---

📌 Prerequisites

Before getting started, ensure you have:

• Python 3.x installed → Download Here
• Basic knowledge of programming concepts

---

📂 Repository Structure

DS-BigO-Complexity/
│── data_structures/        # Implementations of stacks, queues, linked lists, trees, etc.
│── algorithms/             # Sorting, searching, dynamic programming, graph algorithms
│── complexity_analysis/    # Big-O notation, best-case, worst-case, average-case analysis
│── interview_questions/    # Common DSA questions from tech interviews
│── visualizations/         # Graphical representations of sorting & searching algorithms
│── README.md               # Project documentation
└── requirements.txt        # Python dependencies

---

⏳ Understanding Big-O Notation

Big-O notation is used to classify algorithms according to their runtime complexity. Here’s a quick reference:

Complexity	Name	Example
O(1)	Constant Time	Accessing an array index
O(log n)	Logarithmic Time	Binary search
O(n)	Linear Time	Iterating through an array
O(n log n)	Linearithmic Time	Merge Sort, Quick Sort
O(n²)	Quadratic Time	Nested loops (e.g., Bubble Sort)
O(2ⁿ)	Exponential Time	Fibonacci recursion
O(n!)	Factorial Time	Traveling Salesman Problem

---

🛠️ Example: Implementing a Sorting Algorithm

Here’s an implementation of Merge Sort, an O(n log n) sorting algorithm:

def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    
    mid = len(arr) // 2
    left_half = merge_sort(arr[:mid])
    right_half = merge_sort(arr[mid:])
    
    return merge(left_half, right_half)

def merge(left, right):
    sorted_arr = []
    i = j = 0
    
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            sorted_arr.append(left[i])
            i += 1
        else:
            sorted_arr.append(right[j])
            j += 1
    
    sorted_arr.extend(left[i:])
    sorted_arr.extend(right[j:])
    
    return sorted_arr

# Example Usage
arr = [5, 3, 8, 6, 2, 7, 4, 1]
print("Sorted Array:", merge_sort(arr))

Output:

Sorted Array: [1, 2, 3, 4, 5, 6, 7, 8]

---

🔍 Topics Covered

📌 Data Structures

• Arrays & Strings
• Linked Lists (Singly, Doubly, Circular)
• Stacks & Queues
• Hash Tables & Hash Functions
• Trees & Binary Search Trees (BSTs)
• Heaps & Priority Queues
• Graphs (Adjacency List & Matrix)

🔢 Algorithms

• Sorting Algorithms: Bubble, Selection, Insertion, Merge, Quick, Heap Sort
• Searching Algorithms: Linear Search, Binary Search
• Graph Algorithms: BFS, DFS, Dijkstra’s Algorithm
• Dynamic Programming: Fibonacci, Knapsack Problem
• Divide & Conquer: Merge Sort, Quick Sort
• Greedy Algorithms: Huffman Coding, Activity Selection
• Backtracking: N-Queens, Sudoku Solver

---

🏆 Problem-Solving Challenges

📌 The repository includes real-world problems with optimal solutions. Examples:

1️⃣ Find the two numbers in an array that sum up to a target (O(n))
2️⃣ Detect a cycle in a linked list (O(n))
3️⃣ Find the lowest common ancestor (LCA) in a BST (O(log n))
4️⃣ Implement a LRU Cache using a HashMap & Doubly Linked List (O(1))
5️⃣ Solve the N-Queens problem using Backtracking (O(N!))

---

🔥 Sorting Algorithm Visualizations

The repository includes sorting visualizations for algorithms like:

Algorithm	Time Complexity	Visualization
Bubble Sort	O(n²)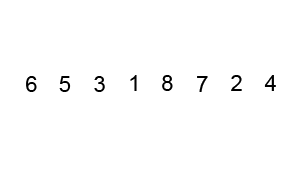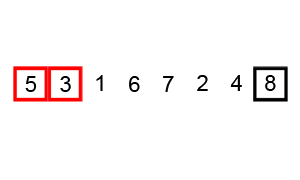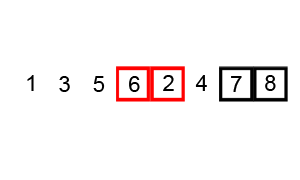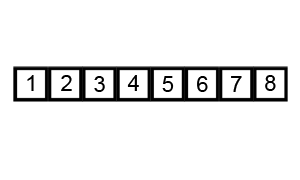
Merge Sort	O(n log n)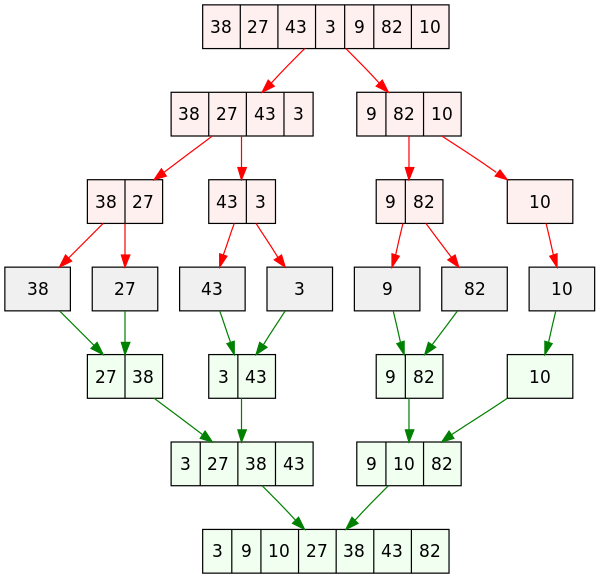
Quick Sort	O(n log n)

---

⚡ How to Run the Code

1️⃣ Clone the Repository

git clone https://github.com/saadsalmanakram/DS-BigO-Complexity.git
cd DS-BigO-Complexity

2️⃣ Install Dependencies

pip install -r requirements.txt

3️⃣ Run Example Scripts

python algorithms/merge_sort.py
python data_structures/linked_list.py

---

🏆 Contributing

Contributions are welcome! 🚀

🔹 Fork the repository
🔹 Create a new branch (git checkout -b feature-name)
🔹 Commit changes (git commit -m "Added new sorting algorithm")
🔹 Push to your branch (git push origin feature-name)
🔹 Open a pull request

---

📜 License

This project is licensed under the MIT License – feel free to use, modify, and share the code.

---

🔗 Resources & References

• Big-O Complexity Cheat Sheet
• MIT Algorithms Course
• CLRS: Introduction to Algorithms

---

📬 Contact

For queries or collaboration, reach out via:

📧 Email: saadsalmanakram1@gmail.com
🌐 GitHub: SaadSalmanAkram
💼 LinkedIn: Saad Salman Akram

---

⚡ Master Data Structures & Algorithms with Confidence! ⚡

---