AES in C

This is a very simple (and NOT a highly optimized and secure) implementation of AES only written to teach you the BASICS of this algorithm.

Advanced Encryption Standard

AES is based on a design principle known as a substitution–permutation network, and is efficient in both software and hardware. Unlike its predecessor DES, AES does not use a Feistel network. AES is a variant of Rijndael, with a fixed block size of 128 bits, and a key size of 128, 192, or 256 bits. By contrast, Rijndael per se is specified with block and key sizes that may be any multiple of 32 bits, with a minimum of 128 and a maximum of 256 bits. Most AES calculations are done in a particular finite field.

AES operates on a 4 × 4 column-major order array of 16 bytes $b_0, b_1, ..., b_15$ termed the state:

$$\begin{bmatrix} b_0 & b_4 & b_8 & b_{12} \\ b_1 & b_5 & b_9 & b_{13} \\ b_2 & b_6 & b_{10} & b_{14} \\ b_3 & b_7 & b_{11} & b_{15} \end{bmatrix}$$

The key size used for an AES cipher specifies the number of transformation rounds that convert the input, called the plaintext, into the final output, called the ciphertext. The number of rounds are as follows:

• 10 rounds for 128-bit keys.
• 12 rounds for 192-bit keys.
• 14 rounds for 256-bit keys.

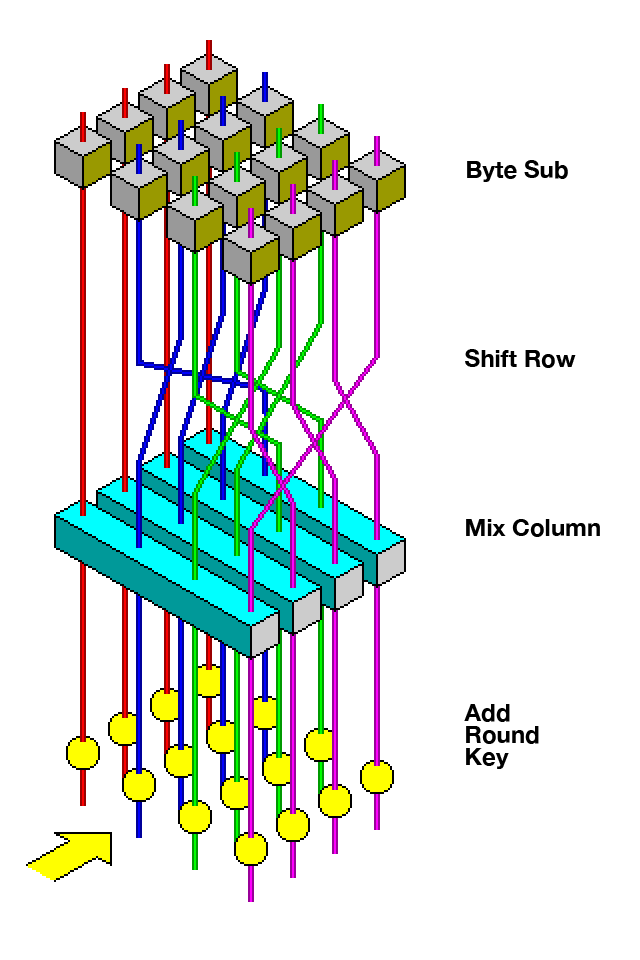
Each round consists of several processing steps, including one that depends on the encryption key itself. A set of reverse rounds are applied to transform ciphertext back into the original plaintext using the same encryption key.

High-level description of the algorithm

1. KeyExpansion – round keys are derived from the cipher key using the AES key schedule. AES requires a separate 128-bit round key block for each round plus one more.
2. Initial round key addition:
   1. AddRoundKey – each byte of the state is combined with a byte of the round key using bitwise xor.
3. 9, 11 or 13 rounds:
   1. SubBytes – a non-linear substitution step where each byte is replaced with another according to a lookup table.
   2. ShiftRows – a transposition step where the last three rows of the state are shifted cyclically a certain number of steps.
   3. MixColumns – a linear mixing operation which operates on the columns of the state, combining the four bytes in each column.
   4. AddRoundKey
4. Final round (making 10, 12 or 14 rounds in total):
   1. SubBytes
   2. ShiftRows
   3. AddRoundKey

The SubBytes step

Rijndael S-box

In the SubBytes step, each byte in the state is replaced with its entry in a fixed 8-bit lookup table, S; bij = S(aij).

---

In the SubBytes step, each byte a ${i,j}$ in the state array is replaced with a SubByte $S(a_{i,j})$ using an 8-bit substitution box. Before round 0, the state array is simply the plaintext/input. This operation provides the non-linearity in the cipher. The S-box used is derived from the multiplicative inverse over GF$(2^8)$, known to have good non-linearity properties. To avoid attacks based on simple algebraic properties, the S-box is constructed by combining the inverse function with an invertible affine transformation. The S-box is also chosen to avoid any fixed points (and so is a derangement), i.e., $S(a_{i,j})\neq a_{i,j}$ , and also any opposite fixed points, i.e., $S(a_{i,j})\oplus a_{i,j}\neq {\text{FF}}_{16}$. While performing the decryption, the InvSubBytes step (the inverse of SubBytes) is used, which requires first taking the inverse of the affine transformation and then finding the multiplicative inverse.

The ShiftRows step

In the ShiftRows step, bytes in each row of the state are shifted cyclically to the left. The number of places each byte is shifted differs incrementally for each row.

---

The ShiftRows step operates on the rows of the state; it cyclically shifts the bytes in each row by a certain offset. For AES, the first row is left unchanged. Each byte of the second row is shifted one to the left. Similarly, the third and fourth rows are shifted by offsets of two and three respectively.[note 6] In this way, each column of the output state of the ShiftRows step is composed of bytes from each column of the input state. The importance of this step is to avoid the columns being encrypted independently, in which case AES would degenerate into four independent block ciphers.

The MixColumns step

Rijndael MixColumns

In the MixColumns step, each column of the state is multiplied with a fixed polynomial $c(x)$

---

In the MixColumns step, the four bytes of each column of the state are combined using an invertible linear transformation. The MixColumns function takes four bytes as input and outputs four bytes, where each input byte affects all four output bytes. Together with ShiftRows, MixColumns provides diffusion in the cipher.

During this operation, each column is transformed using a fixed matrix (matrix left-multiplied by column gives new value of column in the state):

$$\begin{bmatrix} b_{0,j} \\ b_{1,j} \\ b_{2,j} \\ b_{3,j} \end{bmatrix}=\begin{bmatrix} 2 & 3 & 1 & 1 \\ 1 & 2 & 3 & 1 \\ 1 & 1 & 2 & 3 \\ 3 & 1 & 1 & 2 \end{bmatrix} \begin{bmatrix} a_{0,j} \\ a_{1,j} \\ a_{2,j} \\ a_{3,j} \end{bmatrix} \quad 0 \leq j \leq 3 $$

Matrix multiplication is composed of multiplication and addition of the entries. Entries are bytes treated as coefficients of polynomial of order $x^{7}$. Addition is simply XOR. Multiplication is modulo irreducible polynomial $x^{8}+x^{4}+x^{3}+x+1$. If processed bit by bit, then, after shifting, a conditional XOR with 1B16 should be performed if the shifted value is larger than FF16 (overflow must be corrected by subtraction of generating polynomial). These are special cases of the usual multiplication in ${GF}(2^{8})$.

In more general sense, each column is treated as a polynomial over ${GF}(2^{8})$ and is then multiplied modulo ${01}{16}\cdot z^{4}+{01}{16}$ with a fixed polynomial $c(z)={03}{16}\cdot z^{3}+{01}{16}\cdot z^{2}+{01}{16}\cdot z+{02}{16}$. The coefficients are displayed in their hexadecimal equivalent of the binary representation of bit polynomials from ${GF}(2)[x]$. The MixColumns step can also be viewed as a multiplication by the shown particular MDS matrix in the finite field ${GF}(2^{8})$ . This process is described further in the article Rijndael MixColumns.

The AddRoundKey

In the AddRoundKey step, each byte of the state is combined with a byte of the round subkey using the XOR operation (⊕).

---

In the AddRoundKey step, the subkey is combined with the state. For each round, a subkey is derived from the main key using Rijndael's key schedule; each subkey is the same size as the state. The subkey is added by combining of the state with the corresponding byte of the subkey using bitwise XOR.

Build and run the code

Build:

make

Run:

./build/AESIC