Stheno is an implementation of Gaussian process modelling in Python. See also Stheno.jl.
Check out our post about linear models with Stheno and JAX.
Contents:
- Nonlinear Regression in 20 Seconds
- Installation
- Manual
- Examples
- Simple Regression
- Hyperparameter Optimisation with Varz
- Hyperparameter Optimisation with PyTorch
- Decomposition of Prediction
- Learn a Function, Incorporating Prior Knowledge About Its Form
- Multi-Output Regression
- Approximate Integration
- Bayesian Linear Regression
- GPAR
- A GP-RNN Model
- Approximate Multiplication Between GPs
- Sparse Regression
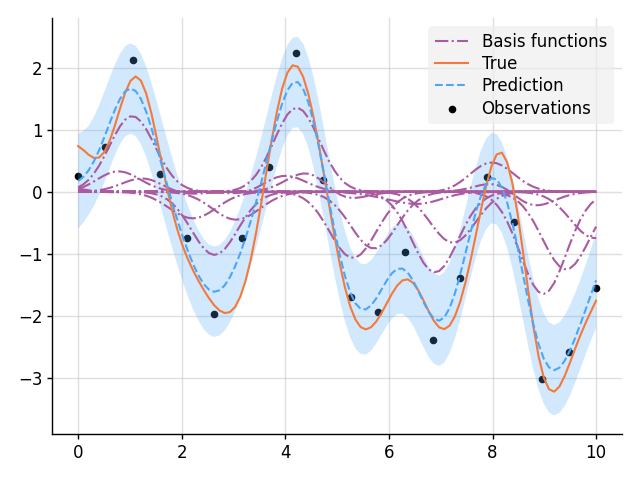
- Smoothing with Nonparametric Basis Functions
>>> import numpy as np
>>> from stheno import GP, EQ
>>> x = np.linspace(0, 2, 10) # Some points to predict at
>>> y = x ** 2 # Some observations
>>> f = GP(EQ()) # Construct Gaussian process.
>>> f_post = f | (f(x), y) # Compute the posterior.
>>> pred = f_post(np.array([1, 2, 3])) # Predict!
>>> pred.mean
<dense matrix: shape=3x1, dtype=float64
mat=[[1. ]
[4. ]
[8.483]]>
>>> pred.var
<dense matrix: shape=3x3, dtype=float64
mat=[[ 8.032e-13 7.772e-16 -4.577e-09]
[ 7.772e-16 9.999e-13 2.773e-10]
[-4.577e-09 2.773e-10 3.313e-03]]>These custom matrix types are there to accelerate the underlying linear algebra.
To get vanilla NumPy/AutoGrad/TensorFlow/PyTorch/JAX arrays, use B.dense:
>>> from lab import B
>>> B.dense(pred.mean)
array([[1.00000068],
[3.99999999],
[8.4825932 ]])
>>> B.dense(pred.var)
array([[ 8.03246358e-13, 7.77156117e-16, -4.57690943e-09],
[ 7.77156117e-16, 9.99866856e-13, 2.77333267e-10],
[-4.57690943e-09, 2.77333267e-10, 3.31283378e-03]])Moar?! Then read on!
pip install stheno
Note: here is a nicely rendered and more readable version of the docs.
from stheno.autograd import GP, EQfrom stheno.tensorflow import GP, EQfrom stheno.torch import GP, EQfrom stheno.jax import GP, EQThe basic building block is a f = GP(mean=0, kernel, measure=prior), which takes
in a mean, a kernel, and a measure.
The mean and kernel of a GP can be extracted with f.mean and f.kernel.
The measure should be thought of as a big joint distribution that assigns a mean and
a kernel to every variable f.
A measure can be created with prior = Measure().
A GP f can have different means and kernels under different measures.
For example, under some prior measure, f can have an EQ() kernel; but, under some
posterior measure, f has a kernel that is determined by the posterior distribution
of a GP.
We will see later how posterior measures can be constructed.
The measure with which a f = GP(kernel, measure=prior) is constructed can be
extracted with f.measure == prior.
If the keyword argument measure is not set, then automatically a new measure is
created, which afterwards can be extracted with f.measure.
Definition, where prior = Measure():
f = GP(kernel)
f = GP(mean, kernel)
f = GP(kernel, measure=prior)
f = GP(mean, kernel, measure=prior)GPs that are associated to the same measure can be combined into new GPs, which is the primary mechanism used to build cool models.
Here's an example model:
>>> prior = Measure()
>>> f1 = GP(lambda x: x ** 2, EQ(), measure=prior)
>>> f1
GP(<lambda>, EQ())
>>> f2 = GP(Linear(), measure=prior)
>>> f2
GP(0, Linear())
>>> f_sum = f1 + f2
>>> f_sum
GP(<lambda>, EQ() + Linear())
>>> f_sum + GP(EQ()) # Not valid: `GP(EQ())` belongs to a new measure!
AssertionError: Processes GP(<lambda>, EQ() + Linear()) and GP(0, EQ()) are associated to different measures.To avoid setting the keyword measure for every GP that you create, you can enter
a measure as a context:
>>> with Measure() as prior:
f1 = GP(lambda x: x ** 2, EQ())
f2 = GP(Linear())
f_sum = f1 + f2
>>> prior == f1.measure == f2.measure == f_sum.measure
True-
Add and subtract GPs and other objects.
Example:
>>> GP(EQ(), measure=prior) + GP(Exp(), measure=prior) GP(0, EQ() + Exp()) >>> GP(EQ(), measure=prior) + GP(EQ(), measure=prior) GP(0, 2 * EQ()) >>> GP(EQ()) + 1 GP(1, EQ()) >>> GP(EQ()) + 0 GP(0, EQ()) >>> GP(EQ()) + (lambda x: x ** 2) GP(<lambda>, EQ()) >>> GP(2, EQ(), measure=prior) - GP(1, EQ(), measure=prior) GP(1, 2 * EQ())
-
Multiply GPs and other objects.
Warning: The product of two GPs it not a Gaussian process. Stheno approximates the resulting process by moment matching.
Example:
>>> GP(1, EQ(), measure=prior) * GP(1, Exp(), measure=prior) GP(<lambda> + <lambda> + -1 * 1, <lambda> * Exp() + <lambda> * EQ() + EQ() * Exp()) >>> 2 * GP(EQ()) GP(2, 2 * EQ()) >>> 0 * GP(EQ()) GP(0, 0) >>> (lambda x: x) * GP(EQ()) GP(0, <lambda> * EQ())
-
Shift GPs.
Example:
>>> GP(EQ()).shift(1) GP(0, EQ() shift 1)
-
Stretch GPs.
Example:
>>> GP(EQ()).stretch(2) GP(0, EQ() > 2)
-
Select particular input dimensions.
Example:
>>> GP(EQ()).select(1, 3) GP(0, EQ() : [1, 3])
-
Transform the input.
Example:
>>> GP(EQ()).transform(f) GP(0, EQ() transform f)
-
Numerically take the derivative of a GP. The argument specifies which dimension to take the derivative with respect to.
Example:
>>> GP(EQ()).diff(1) GP(0, d(1) EQ())
-
Construct a finite difference estimate of the derivative of a GP. See
Measure.diff_approxfor a description of the arguments.Example:
>>> GP(EQ()).diff_approx(deriv=1, order=2) GP(50000000.0 * (0.5 * EQ() + 0.5 * ((-0.5 * (EQ() shift (0.0001414213562373095, 0))) shift (0, -0.0001414213562373095)) + 0.5 * ((-0.5 * (EQ() shift (0, 0.0001414213562373095))) shift (-0.0001414213562373095, 0))), 0)
-
Construct the Cartesian product of a collection of GPs.
Example:
>>> prior = Measure() >>> f1, f2 = GP(EQ(), measure=prior), GP(EQ(), measure=prior) >>> cross(f1, f2) GP(MultiOutputMean(0, 0), MultiOutputKernel(EQ(), EQ()))
GPs have a display method that accepts a formatter.
Example:
>>> print(GP(2.12345 * EQ()).display(lambda x: f"{x:.2f}"))
GP(2.12 * EQ(), 0)Properties of kernels can be queried on GPs directly.
Example:
>>> GP(EQ()).stationary
TrueIt is possible to give a name to a GP. Names must be strings. A measure then behaves like a two-way dictionary between GPs and their names.
Example:
>>> prior = Measure()
>>> p = GP(EQ(), name="name", measure=prior)
>>> p.name
'name'
>>> p.name = "alternative_name"
>>> prior["alternative_name"]
GP(0, EQ())
>>> prior[p]
'alternative_name'Simply call a GP to construct a finite-dimensional distribution at some inputs. You can give a second argument, which specifies the variance of additional additive noise. After constructing a finite-dimensional distribution, you can compute the mean, the variance, sample, or compute a logpdf.
Definition, where f is a GP:
f(x) # No additional noise
f(x, noise) # Additional noise with variance `noise`Things you can do with a finite-dimensional distribution:
-
Use
f(x).meanto compute the mean. -
Use
f(x).varto compute the variance. -
Use
f(x).mean_varto compute simultaneously compute the mean and variance. This can be substantially more efficient than calling firstf(x).meanand thenf(x).var. -
Use
Normal.sampleto sample.Definition:
f(x).sample() # Produce one sample. f(x).sample(n) # Produce `n` samples. f(x).sample(noise=noise) # Produce one samples with additional noise variance `noise`. f(x).sample(n, noise=noise) # Produce `n` samples with additional noise variance `noise`.
-
Use
f(x).logpdf(y)to compute the logpdf of some datay. -
Use
means, variances = f(x).marginals()to efficiently compute the marginal means and marginal variances.Example:
>>> f(x).marginals() (array([0., 0., 0.]), np.array([1., 1., 1.]))
-
Use
means, lowers, uppers = f(x).marginal_credible_bounds()to efficiently compute the means and the marginal lower and upper 95% central credible region bounds.Example:
>>> f(x).marginal_credible_bounds() (array([0., 0., 0.]), array([-1.96, -1.96, -1.96]), array([1.96, 1.96, 1.96]))
-
Use
Measure.logpdfto compute the joint logpdf of multiple observations.Definition, where
prior = Measure():prior.logpdf(f(x), y) prior.logpdf((f1(x1), y1), (f2(x2), y2), ...)
-
Use
Measure.sampleto jointly sample multiple observations.Definition, where
prior = Measure():sample = prior.sample(f(x)) sample1, sample2, ... = prior.sample(f1(x1), f2(x2), ...)
Example:
>>> prior = Measure()
>>> f = GP(EQ(), measure=prior)
>>> x = np.array([0., 1., 2.])
>>> f(x) # FDD without noise.
<FDD:
process=GP(0, EQ()),
input=array([0., 1., 2.]),
noise=<zero matrix: shape=3x3, dtype=float64>
>>> f(x, 0.1) # FDD with noise.
<FDD:
process=GP(0, EQ()),
input=array([0., 1., 2.]),
noise=<diagonal matrix: shape=3x3, dtype=float64
diag=[0.1 0.1 0.1]>>
>>> f(x).mean
array([[0.],
[0.],
[0.]])
>>> f(x).var
<dense matrix: shape=3x3, dtype=float64
mat=[[1. 0.607 0.135]
[0.607 1. 0.607]
[0.135 0.607 1. ]]>
>>> y1 = f(x).sample()
>>> y1
array([[-0.45172746],
[ 0.46581948],
[ 0.78929767]])
>>> f(x).logpdf(y1)
-2.811609567720761
>>> y2 = f(x).sample(2)
array([[-0.43771276, -2.36741858],
[ 0.86080043, -1.22503079],
[ 2.15779126, -0.75319405]]
>>> f(x).logpdf(y2)
array([-4.82949038, -5.40084225])Conditioning a prior measure on observations gives a posterior measure.
To condition a measure on observations, use Measure.__or__.
Definition, where prior = Measure() and f* are GPs:
post = prior | (f(x, [noise]), y)
post = prior | ((f1(x1, [noise1]), y1), (f2(x2, [noise2]), y2), ...)You can then obtain a posterior process with post(f) and a finite-dimensional
distribution under the posterior with post(f(x)).
Alternatively, the posterior of a process f can be obtained by conditioning f
directly.
Definition, where and f* are GPs:
f_post = f | (f(x, [noise]), y)
f_post = f | ((f1(x1, [noise1]), y1), (f2(x2, [noise2]), y2), ...)Let's consider an example. First, build a model and sample some values.
>>> prior = Measure()
>>> f = GP(EQ(), measure=prior)
>>> x = np.array([0., 1., 2.])
>>> y = f(x).sample()Then compute the posterior measure.
>>> post = prior | (f(x), y)
>>> post(f)
GP(PosteriorMean(), PosteriorKernel())
>>> post(f).mean(x)
<dense matrix: shape=3x1, dtype=float64
mat=[[ 0.412]
[-0.811]
[-0.933]]>
>>> post(f).kernel(x)
<dense matrix: shape=3x3, dtype=float64
mat=[[1.e-12 0.e+00 0.e+00]
[0.e+00 1.e-12 0.e+00]
[0.e+00 0.e+00 1.e-12]]>
>>> post(f(x))
<FDD:
process=GP(PosteriorMean(), PosteriorKernel()),
input=array([0., 1., 2.]),
noise=<zero matrix: shape=3x3, dtype=float64>>
>>> post(f(x)).mean
<dense matrix: shape=3x1, dtype=float64
mat=[[ 0.412]
[-0.811]
[-0.933]]>
>>> post(f(x)).var
<dense matrix: shape=3x3, dtype=float64
mat=[[1.e-12 0.e+00 0.e+00]
[0.e+00 1.e-12 0.e+00]
[0.e+00 0.e+00 1.e-12]]>We can also obtain the posterior by conditioning f directly:
>>> f_post = f | (f(x), y)
>>> f_post
GP(PosteriorMean(), PosteriorKernel())
>>> f_post.mean(x)
<dense matrix: shape=3x1, dtype=float64
mat=[[ 0.412]
[-0.811]
[-0.933]]>
>>> f_post.kernel(x)
<dense matrix: shape=3x3, dtype=float64
mat=[[1.e-12 0.e+00 0.e+00]
[0.e+00 1.e-12 0.e+00]
[0.e+00 0.e+00 1.e-12]]>
>>> f_post(x)
<FDD:
process=GP(PosteriorMean(), PosteriorKernel()),
input=array([0., 1., 2.]),
noise=<zero matrix: shape=3x3, dtype=float64>>
>>> f_post(x).mean
<dense matrix: shape=3x1, dtype=float64
mat=[[ 0.412]
[-0.811]
[-0.933]]>
>>> f_post(x).var
<dense matrix: shape=3x3, dtype=float64
mat=[[1.e-12 0.e+00 0.e+00]
[0.e+00 1.e-12 0.e+00]
[0.e+00 0.e+00 1.e-12]]>We can further extend our model by building on the posterior.
>>> g = GP(Linear(), measure=post)
>>> f_sum = post(f) + g
>>> f_sum
GP(PosteriorMean(), PosteriorKernel() + Linear())However, what we cannot do is mixing the prior and posterior.
>>> f + g
AssertionError: Processes GP(0, EQ()) and GP(0, Linear()) are associated to different measures.Stheno supports pseudo-point approximations of posterior distributions with various approximation methods:
-
The Variational Free Energy (VFE; Titsias, 2009) approximation. To use the VFE approximation, use
PseudoObs. -
The Fully Independent Training Conditional (FITC; Snelson & Ghahramani, 2006) approximation. To use the FITC approximation, use
PseudoObsFITC. -
The Deterministic Training Conditional (DTC; Csato & Opper, 2002; Seeger et al., 2003) approximation. To use the DTC approximation, use
PseudoObsDTC.
The VFE approximation (PseudoObs) is the approximation recommended to use.
The following definitions and examples will use the VFE approximation with PseudoObs,
but every instance of PseudoObs can be swapped out for PseudoObsFITC or
PseudoObsDTC.
Definition:
obs = PseudoObs(
u(z), # FDD of inducing points
(f(x, [noise]), y) # Observed data
)
obs = PseudoObs(u(z), f(x, [noise]), y)
obs = PseudoObs(u(z), (f1(x1, [noise1]), y1), (f2(x2, [noise2]), y2), ...)
obs = PseudoObs((u1(z1), u2(z2), ...), f(x, [noise]), y)
obs = PseudoObs((u1(z1), u2(z2), ...), (f1(x1, [noise1]), y1), (f2(x2, [noise2]), y2), ...)The approximate posterior measure can be constructed with prior | obs
where prior = Measure() is the measure of your model.
To quantify the quality of the approximation, you can compute the ELBO with
obs.elbo(prior).
Let's consider an example. First, build a model and sample some noisy observations.
>>> prior = Measure()
>>> f = GP(EQ(), measure=prior)
>>> x_obs = np.linspace(0, 10, 2000)
>>> y_obs = f(x_obs, 1).sample()Ouch, computing the logpdf is quite slow:
>>> %timeit f(x_obs, 1).logpdf(y_obs)
219 ms ± 35.7 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)Let's try to use inducing points to speed this up.
>>> x_ind = np.linspace(0, 10, 100)
>>> u = f(x_ind) # FDD of inducing points.
>>> %timeit PseudoObs(u, f(x_obs, 1), y_obs).elbo(prior)
9.8 ms ± 181 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)Much better. And the approximation is good:
>>> PseudoObs(u, f(x_obs, 1), y_obs).elbo(prior) - f(x_obs, 1).logpdf(y_obs)
-3.537934389896691e-10We finally construct the approximate posterior measure:
>>> post_approx = prior | PseudoObs(u, f(x_obs, 1), y_obs)
>>> post_approx(f(x_obs)).mean
<dense matrix: shape=2000x1, dtype=float64
mat=[[0.469]
[0.468]
[0.467]
...
[1.09 ]
[1.09 ]
[1.091]]>See MLKernels.
Stheno supports batched computation. See MLKernels for a description of how means and kernels work with batched computation.
Example:
>>> f = GP(EQ())
>>> x = np.random.randn(16, 100, 1)
>>> y = f(x, 1).sample()
>>> logpdf = f(x, 1).logpdf(y)
>>> y.shape
(16, 100, 1)
>>> f(x, 1).logpdf(y).shape
(16,)Stheno uses LAB to provide an implementation that is backend agnostic. Moreover, Stheno uses an extension of LAB to accelerate linear algebra with structured linear algebra primitives. You will encounter these primitives:
>>> k = 2 * Delta()
>>> x = np.linspace(0, 5, 10)
>>> k(x)
<diagonal matrix: shape=10x10, dtype=float64
diag=[2. 2. 2. 2. 2. 2. 2. 2. 2. 2.]>If you're using LAB to further process these matrices, then there is absolutely no need to worry: these structured matrix types know how to add, multiply, and do other linear algebra operations.
>>> import lab as B
>>> B.matmul(k(x), k(x))
<diagonal matrix: shape=10x10, dtype=float64
diag=[4. 4. 4. 4. 4. 4. 4. 4. 4. 4.]>If you're not using LAB, you can convert these
structured primitives to regular NumPy/TensorFlow/PyTorch/JAX arrays by calling
B.dense (B is from LAB):
>>> import lab as B
>>> B.dense(k(x))
array([[2., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 2., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 2., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 2., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 2., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 2., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 2., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 2., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 2., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 2.]])Furthermore, before computing a Cholesky decomposition, Stheno always adds a minuscule
diagonal to prevent the Cholesky decomposition from failing due to positive
indefiniteness caused by numerical noise.
You can change the magnitude of this diagonal by changing B.epsilon:
>>> import lab as B
>>> B.epsilon = 1e-12 # Default regularisation
>>> B.epsilon = 1e-8 # Strong regularisationThe examples make use of Varz and some utility from WBML.
import matplotlib.pyplot as plt
from wbml.plot import tweak
from stheno import B, GP, EQ
# Define points to predict at.
x = B.linspace(0, 10, 100)
x_obs = B.linspace(0, 7, 20)
# Construct a prior.
f = GP(EQ().periodic(5.0))
# Sample a true, underlying function and noisy observations.
f_true, y_obs = f.measure.sample(f(x), f(x_obs, 0.5))
# Now condition on the observations to make predictions.
f_post = f | (f(x_obs, 0.5), y_obs)
mean, lower, upper = f_post(x).marginal_credible_bounds()
# Plot result.
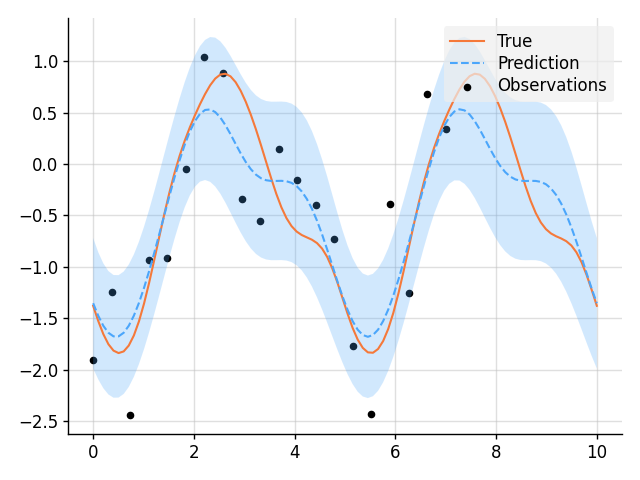
plt.plot(x, f_true, label="True", style="test")
plt.scatter(x_obs, y_obs, label="Observations", style="train", s=20)
plt.plot(x, mean, label="Prediction", style="pred")
plt.fill_between(x, lower, upper, style="pred")
tweak()
plt.savefig("readme_example1_simple_regression.png")
plt.show()import lab as B
import matplotlib.pyplot as plt
import torch
from varz import Vars, minimise_l_bfgs_b, parametrised, Positive
from wbml.plot import tweak
from stheno.torch import EQ, GP
# Increase regularisation because PyTorch defaults to 32-bit floats.
B.epsilon = 1e-6
# Define points to predict at.
x = torch.linspace(0, 2, 100)
x_obs = torch.linspace(0, 2, 50)
# Sample a true, underlying function and observations with observation noise `0.05`.
f_true = torch.sin(5 * x)
y_obs = torch.sin(5 * x_obs) + 0.05**0.5 * torch.randn(50)
def model(vs):
"""Construct a model with learnable parameters."""
p = vs.struct # Varz handles positivity (and other) constraints.
kernel = p.variance.positive() * EQ().stretch(p.scale.positive())
return GP(kernel), p.noise.positive()
@parametrised
def model_alternative(vs, scale: Positive, variance: Positive, noise: Positive):
"""Equivalent to :func:`model`, but with `@parametrised`."""
kernel = variance * EQ().stretch(scale)
return GP(kernel), noise
vs = Vars(torch.float32)
f, noise = model(vs)
# Condition on observations and make predictions before optimisation.
f_post = f | (f(x_obs, noise), y_obs)
prior_before = f, noise
pred_before = f_post(x, noise).marginal_credible_bounds()
def objective(vs):
f, noise = model(vs)
evidence = f(x_obs, noise).logpdf(y_obs)
return -evidence
# Learn hyperparameters.
minimise_l_bfgs_b(objective, vs)
f, noise = model(vs)
# Condition on observations and make predictions after optimisation.
f_post = f | (f(x_obs, noise), y_obs)
prior_after = f, noise
pred_after = f_post(x, noise).marginal_credible_bounds()
def plot_prediction(prior, pred):
f, noise = prior
mean, lower, upper = pred
plt.scatter(x_obs, y_obs, label="Observations", style="train", s=20)
plt.plot(x, f_true, label="True", style="test")
plt.plot(x, mean, label="Prediction", style="pred")
plt.fill_between(x, lower, upper, style="pred")
plt.ylim(-2, 2)
plt.text(
0.02,
0.02,
f"var = {f.kernel.factor(0):.2f}, "
f"scale = {f.kernel.factor(1).stretches[0]:.2f}, "
f"noise = {noise:.2f}",
transform=plt.gca().transAxes,
)
tweak()
# Plot result.
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
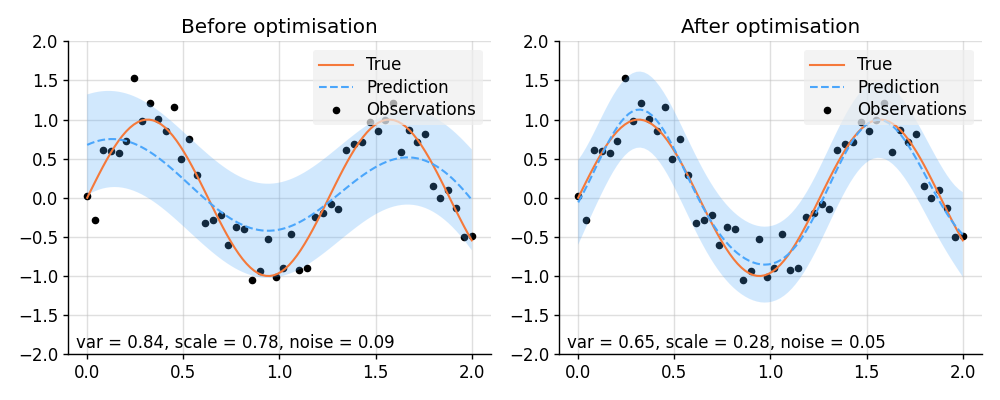
plt.title("Before optimisation")
plot_prediction(prior_before, pred_before)
plt.subplot(1, 2, 2)
plt.title("After optimisation")
plot_prediction(prior_after, pred_after)
plt.savefig("readme_example12_optimisation_varz.png")
plt.show()import lab as B
import matplotlib.pyplot as plt
import torch
from wbml.plot import tweak
from stheno.torch import EQ, GP
# Increase regularisation because PyTorch defaults to 32-bit floats.
B.epsilon = 1e-6
# Define points to predict at.
x = torch.linspace(0, 2, 100)
x_obs = torch.linspace(0, 2, 50)
# Sample a true, underlying function and observations with observation noise `0.05`.
f_true = torch.sin(5 * x)
y_obs = torch.sin(5 * x_obs) + 0.05**0.5 * torch.randn(50)
class Model(torch.nn.Module):
"""A GP model with learnable parameters."""
def __init__(self, init_var=0.3, init_scale=1, init_noise=0.2):
super().__init__()
# Ensure that the parameters are positive and make them learnable.
self.log_var = torch.nn.Parameter(torch.log(torch.tensor(init_var)))
self.log_scale = torch.nn.Parameter(torch.log(torch.tensor(init_scale)))
self.log_noise = torch.nn.Parameter(torch.log(torch.tensor(init_noise)))
def construct(self):
self.var = torch.exp(self.log_var)
self.scale = torch.exp(self.log_scale)
self.noise = torch.exp(self.log_noise)
kernel = self.var * EQ().stretch(self.scale)
return GP(kernel), self.noise
model = Model()
f, noise = model.construct()
# Condition on observations and make predictions before optimisation.
f_post = f | (f(x_obs, noise), y_obs)
prior_before = f, noise
pred_before = f_post(x, noise).marginal_credible_bounds()
# Perform optimisation.
opt = torch.optim.Adam(model.parameters(), lr=5e-2)
for _ in range(1000):
opt.zero_grad()
f, noise = model.construct()
loss = -f(x_obs, noise).logpdf(y_obs)
loss.backward()
opt.step()
f, noise = model.construct()
# Condition on observations and make predictions after optimisation.
f_post = f | (f(x_obs, noise), y_obs)
prior_after = f, noise
pred_after = f_post(x, noise).marginal_credible_bounds()
def plot_prediction(prior, pred):
f, noise = prior
mean, lower, upper = pred
plt.scatter(x_obs, y_obs, label="Observations", style="train", s=20)
plt.plot(x, f_true, label="True", style="test")
plt.plot(x, mean, label="Prediction", style="pred")
plt.fill_between(x, lower, upper, style="pred")
plt.ylim(-2, 2)
plt.text(
0.02,
0.02,
f"var = {f.kernel.factor(0):.2f}, "
f"scale = {f.kernel.factor(1).stretches[0]:.2f}, "
f"noise = {noise:.2f}",
transform=plt.gca().transAxes,
)
tweak()
# Plot result.
plt.figure(figsize=(10, 4))
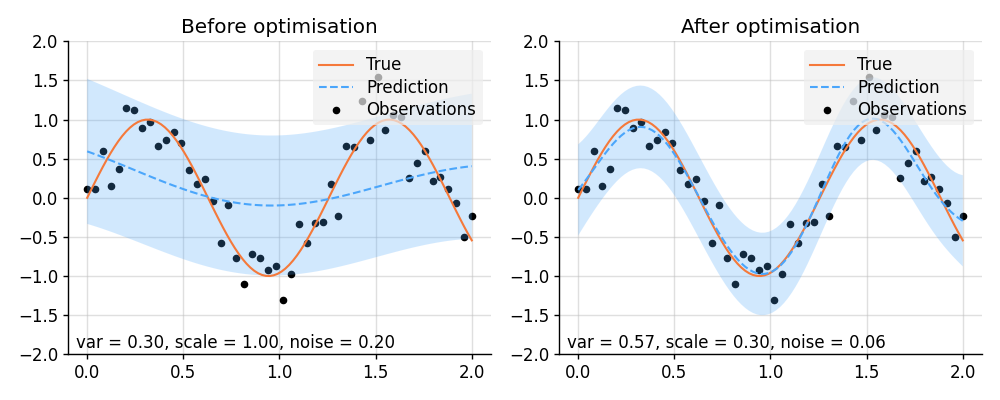
plt.subplot(1, 2, 1)
plt.title("Before optimisation")
plot_prediction(prior_before, pred_before)
plt.subplot(1, 2, 2)
plt.title("After optimisation")
plot_prediction(prior_after, pred_after)
plt.savefig("readme_example13_optimisation_torch.png")
plt.show()import matplotlib.pyplot as plt
from wbml.plot import tweak
from stheno import Measure, GP, EQ, RQ, Linear, Delta, Exp, B
B.epsilon = 1e-10
# Define points to predict at.
x = B.linspace(0, 10, 200)
x_obs = B.linspace(0, 7, 50)
with Measure() as prior:
# Construct a latent function consisting of four different components.
f_smooth = GP(EQ())
f_wiggly = GP(RQ(1e-1).stretch(0.5))
f_periodic = GP(EQ().periodic(1.0))
f_linear = GP(Linear())
f = f_smooth + f_wiggly + f_periodic + 0.2 * f_linear
# Let the observation noise consist of a bit of exponential noise.
e_indep = GP(Delta())
e_exp = GP(Exp())
e = e_indep + 0.3 * e_exp
# Sum the latent function and observation noise to get a model for the observations.
y = f + 0.5 * e
# Sample a true, underlying function and observations.
(
f_true_smooth,
f_true_wiggly,
f_true_periodic,
f_true_linear,
f_true,
y_obs,
) = prior.sample(f_smooth(x), f_wiggly(x), f_periodic(x), f_linear(x), f(x), y(x_obs))
# Now condition on the observations and make predictions for the latent function and
# its various components.
post = prior | (y(x_obs), y_obs)
pred_smooth = post(f_smooth(x))
pred_wiggly = post(f_wiggly(x))
pred_periodic = post(f_periodic(x))
pred_linear = post(f_linear(x))
pred_f = post(f(x))
# Plot results.
def plot_prediction(x, f, pred, x_obs=None, y_obs=None):
plt.plot(x, f, label="True", style="test")
if x_obs is not None:
plt.scatter(x_obs, y_obs, label="Observations", style="train", s=20)
mean, lower, upper = pred.marginal_credible_bounds()
plt.plot(x, mean, label="Prediction", style="pred")
plt.fill_between(x, lower, upper, style="pred")
tweak()
plt.figure(figsize=(10, 6))
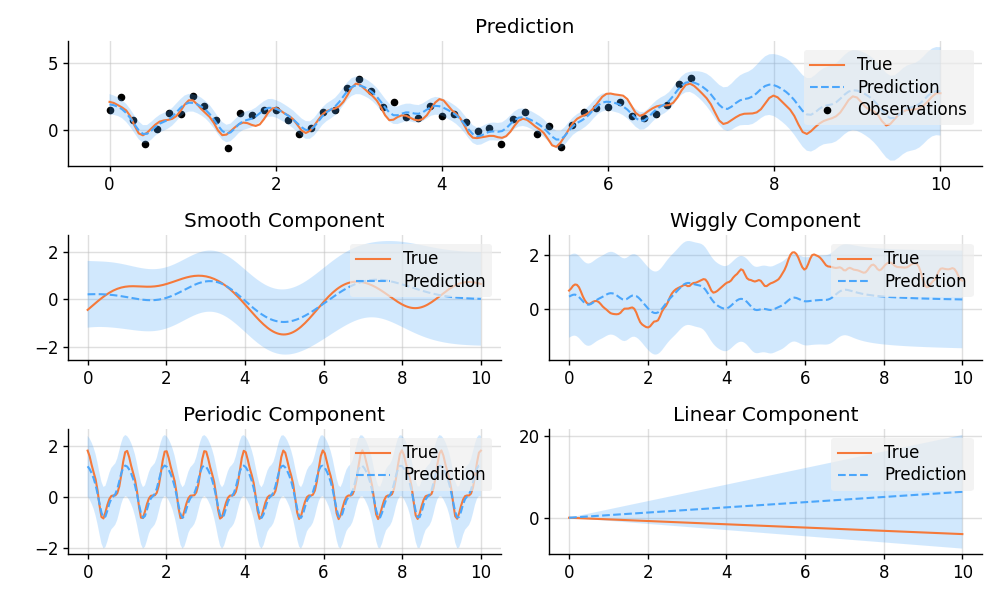
plt.subplot(3, 1, 1)
plt.title("Prediction")
plot_prediction(x, f_true, pred_f, x_obs, y_obs)
plt.subplot(3, 2, 3)
plt.title("Smooth Component")
plot_prediction(x, f_true_smooth, pred_smooth)
plt.subplot(3, 2, 4)
plt.title("Wiggly Component")
plot_prediction(x, f_true_wiggly, pred_wiggly)
plt.subplot(3, 2, 5)
plt.title("Periodic Component")
plot_prediction(x, f_true_periodic, pred_periodic)
plt.subplot(3, 2, 6)
plt.title("Linear Component")
plot_prediction(x, f_true_linear, pred_linear)
plt.savefig("readme_example2_decomposition.png")
plt.show()import matplotlib.pyplot as plt
import tensorflow as tf
import wbml.out as out
from varz.spec import parametrised, Positive
from varz.tensorflow import Vars, minimise_l_bfgs_b
from wbml.plot import tweak
from stheno.tensorflow import B, Measure, GP, EQ, Delta
# Define points to predict at.
x = B.linspace(tf.float64, 0, 5, 100)
x_obs = B.linspace(tf.float64, 0, 3, 20)
@parametrised
def model(
vs,
u_var: Positive = 0.5,
u_scale: Positive = 0.5,
noise: Positive = 0.5,
alpha: Positive = 1.2,
):
with Measure():
# Random fluctuation:
u = GP(u_var * EQ().stretch(u_scale))
# Construct model.
f = u + (lambda x: x**alpha)
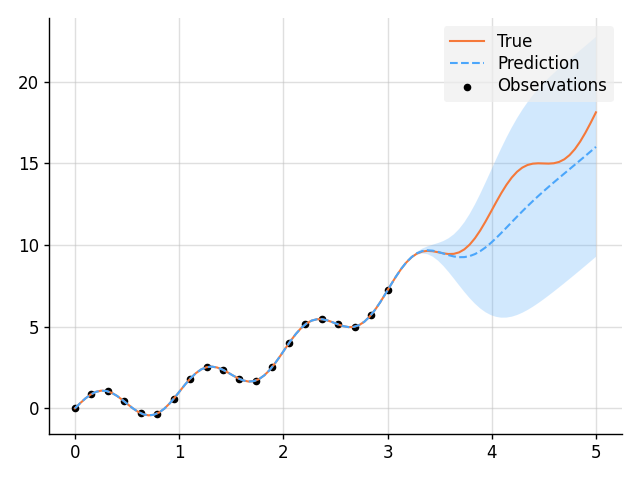
return f, noise
# Sample a true, underlying function and observations.
vs = Vars(tf.float64)
f_true = x**1.8 + B.sin(2 * B.pi * x)
f, y = model(vs)
post = f.measure | (f(x), f_true)
y_obs = post(f(x_obs)).sample()
def objective(vs):
f, noise = model(vs)
evidence = f(x_obs, noise).logpdf(y_obs)
return -evidence
# Learn hyperparameters.
minimise_l_bfgs_b(objective, vs, jit=True)
f, noise = model(vs)
# Print the learned parameters.
out.kv("Prior", f.display(out.format))
vs.print()
# Condition on the observations to make predictions.
f_post = f | (f(x_obs, noise), y_obs)
mean, lower, upper = f_post(x).marginal_credible_bounds()
# Plot result.
plt.plot(x, B.squeeze(f_true), label="True", style="test")
plt.scatter(x_obs, B.squeeze(y_obs), label="Observations", style="train", s=20)
plt.plot(x, mean, label="Prediction", style="pred")
plt.fill_between(x, lower, upper, style="pred")
tweak()
plt.savefig("readme_example3_parametric.png")
plt.show()import matplotlib.pyplot as plt
from wbml.plot import tweak
from stheno import B, Measure, GP, EQ, Delta
class VGP:
"""A vector-valued GP."""
def __init__(self, ps):
self.ps = ps
def __add__(self, other):
return VGP([f + g for f, g in zip(self.ps, other.ps)])
def lmatmul(self, A):
m, n = A.shape
ps = [0 for _ in range(m)]
for i in range(m):
for j in range(n):
ps[i] += A[i, j] * self.ps[j]
return VGP(ps)
# Define points to predict at.
x = B.linspace(0, 10, 100)
x_obs = B.linspace(0, 10, 10)
# Model parameters:
m = 2
p = 4
H = B.randn(p, m)
with Measure() as prior:
# Construct latent functions.
us = VGP([GP(EQ()) for _ in range(m)])
# Construct multi-output prior.
fs = us.lmatmul(H)
# Construct noise.
e = VGP([GP(0.5 * Delta()) for _ in range(p)])
# Construct observation model.
ys = e + fs
# Sample a true, underlying function and observations.
samples = prior.sample(*(p(x) for p in fs.ps), *(p(x_obs) for p in ys.ps))
fs_true, ys_obs = samples[:p], samples[p:]
# Compute the posterior and make predictions.
post = prior.condition(*((p(x_obs), y_obs) for p, y_obs in zip(ys.ps, ys_obs)))
preds = [post(p(x)) for p in fs.ps]
# Plot results.
def plot_prediction(x, f, pred, x_obs=None, y_obs=None):
plt.plot(x, f, label="True", style="test")
if x_obs is not None:
plt.scatter(x_obs, y_obs, label="Observations", style="train", s=20)
mean, lower, upper = pred.marginal_credible_bounds()
plt.plot(x, mean, label="Prediction", style="pred")
plt.fill_between(x, lower, upper, style="pred")
tweak()
plt.figure(figsize=(10, 6))
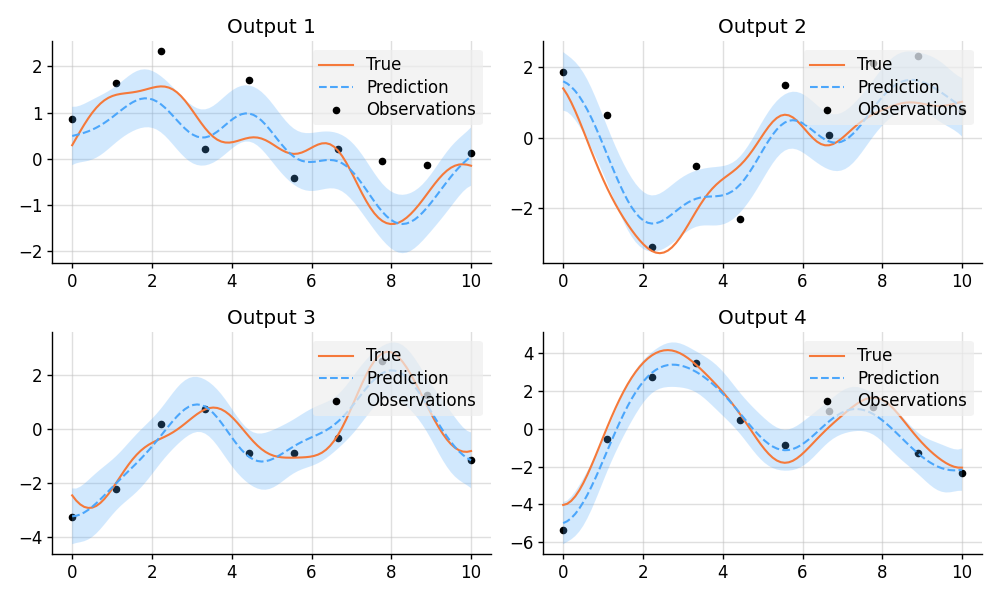
for i in range(4):
plt.subplot(2, 2, i + 1)
plt.title(f"Output {i + 1}")
plot_prediction(x, fs_true[i], preds[i], x_obs, ys_obs[i])
plt.savefig("readme_example4_multi-output.png")
plt.show()import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
import wbml.plot
from stheno.tensorflow import B, Measure, GP, EQ, Delta
# Define points to predict at.
x = B.linspace(tf.float64, 0, 10, 200)
x_obs = B.linspace(tf.float64, 0, 10, 10)
with Measure() as prior:
# Construct a model.
f = 0.7 * GP(EQ()).stretch(1.5)
e = 0.2 * GP(Delta())
# Construct derivatives.
df = f.diff()
ddf = df.diff()
dddf = ddf.diff() + e
# Fix the integration constants.
zero = B.cast(tf.float64, 0)
one = B.cast(tf.float64, 1)
prior = prior | ((f(zero), one), (df(zero), zero), (ddf(zero), -one))
# Sample observations.
y_obs = B.sin(x_obs) + 0.2 * B.randn(*x_obs.shape)
# Condition on the observations to make predictions.
post = prior | (dddf(x_obs), y_obs)
# And make predictions.
pred_iiif = post(f)(x)
pred_iif = post(df)(x)
pred_if = post(ddf)(x)
pred_f = post(dddf)(x)
# Plot result.
def plot_prediction(x, f, pred, x_obs=None, y_obs=None):
plt.plot(x, f, label="True", style="test")
if x_obs is not None:
plt.scatter(x_obs, y_obs, label="Observations", style="train", s=20)
mean, lower, upper = pred.marginal_credible_bounds()
plt.plot(x, mean, label="Prediction", style="pred")
plt.fill_between(x, lower, upper, style="pred")
wbml.plot.tweak()
plt.figure(figsize=(10, 6))
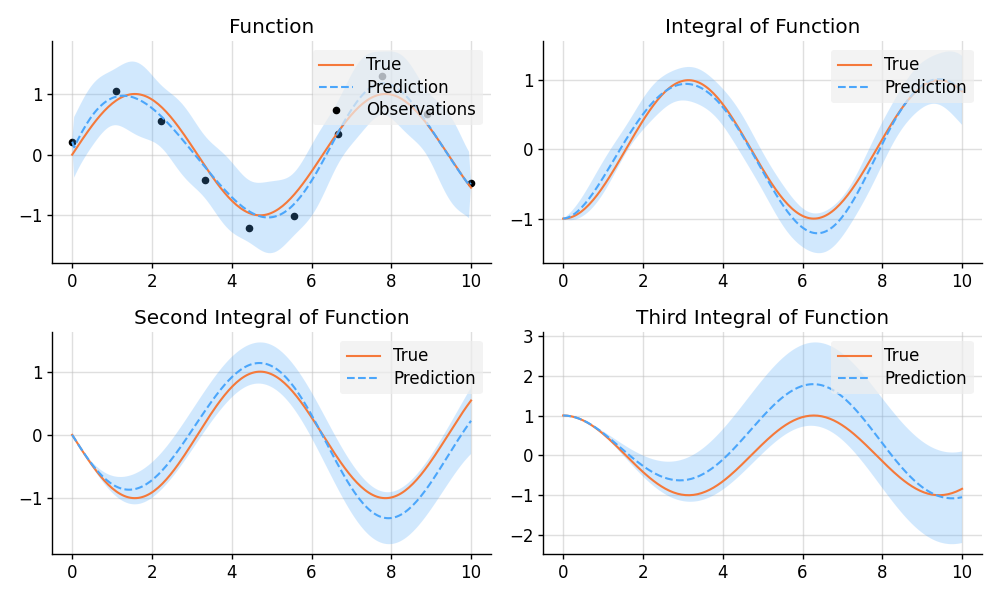
plt.subplot(2, 2, 1)
plt.title("Function")
plot_prediction(x, np.sin(x), pred_f, x_obs=x_obs, y_obs=y_obs)
plt.subplot(2, 2, 2)
plt.title("Integral of Function")
plot_prediction(x, -np.cos(x), pred_if)
plt.subplot(2, 2, 3)
plt.title("Second Integral of Function")
plot_prediction(x, -np.sin(x), pred_iif)
plt.subplot(2, 2, 4)
plt.title("Third Integral of Function")
plot_prediction(x, np.cos(x), pred_iiif)
plt.savefig("readme_example5_integration.png")
plt.show()import matplotlib.pyplot as plt
import wbml.out as out
from wbml.plot import tweak
from stheno import B, Measure, GP
B.epsilon = 1e-10 # Very slightly regularise.
# Define points to predict at.
x = B.linspace(0, 10, 200)
x_obs = B.linspace(0, 10, 10)
with Measure() as prior:
# Construct a linear model.
slope = GP(1)
intercept = GP(5)
f = slope * (lambda x: x) + intercept
# Sample a slope, intercept, underlying function, and observations.
true_slope, true_intercept, f_true, y_obs = prior.sample(
slope(0), intercept(0), f(x), f(x_obs, 0.2)
)
# Condition on the observations to make predictions.
post = prior | (f(x_obs, 0.2), y_obs)
mean, lower, upper = post(f(x)).marginal_credible_bounds()
out.kv("True slope", true_slope[0, 0])
out.kv("Predicted slope", post(slope(0)).mean[0, 0])
out.kv("True intercept", true_intercept[0, 0])
out.kv("Predicted intercept", post(intercept(0)).mean[0, 0])
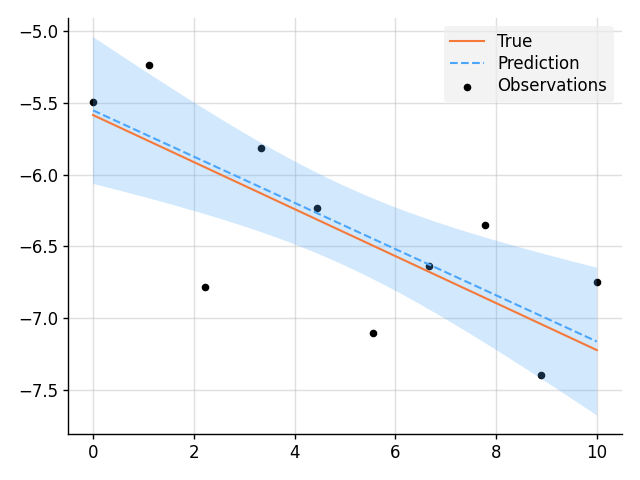
# Plot result.
plt.plot(x, f_true, label="True", style="test")
plt.scatter(x_obs, y_obs, label="Observations", style="train", s=20)
plt.plot(x, mean, label="Prediction", style="pred")
plt.fill_between(x, lower, upper, style="pred")
tweak()
plt.savefig("readme_example6_blr.png")
plt.show()import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from varz.spec import parametrised, Positive
from varz.tensorflow import Vars, minimise_l_bfgs_b
from wbml.plot import tweak
from stheno.tensorflow import B, GP, EQ
# Define points to predict at.
x = B.linspace(tf.float64, 0, 10, 200)
x_obs1 = B.linspace(tf.float64, 0, 10, 30)
inds2 = np.random.permutation(len(x_obs1))[:10]
x_obs2 = B.take(x_obs1, inds2)
# Construction functions to predict and observations.
f1_true = B.sin(x)
f2_true = B.sin(x) ** 2
y1_obs = B.sin(x_obs1) + 0.1 * B.randn(*x_obs1.shape)
y2_obs = B.sin(x_obs2) ** 2 + 0.1 * B.randn(*x_obs2.shape)
@parametrised
def model(
vs,
var1: Positive = 1,
scale1: Positive = 1,
noise1: Positive = 0.1,
var2: Positive = 1,
scale2: Positive = 1,
noise2: Positive = 0.1,
):
# Build layers:
f1 = GP(var1 * EQ().stretch(scale1))
f2 = GP(var2 * EQ().stretch(scale2))
return (f1, noise1), (f2, noise2)
def objective(vs):
(f1, noise1), (f2, noise2) = model(vs)
x1 = x_obs1
x2 = B.stack(x_obs2, B.take(y1_obs, inds2), axis=1)
evidence = f1(x1, noise1).logpdf(y1_obs) + f2(x2, noise2).logpdf(y2_obs)
return -evidence
# Learn hyperparameters.
vs = Vars(tf.float64)
minimise_l_bfgs_b(objective, vs)
# Compute posteriors.
(f1, noise1), (f2, noise2) = model(vs)
x1 = x_obs1
x2 = B.stack(x_obs2, B.take(y1_obs, inds2), axis=1)
f1_post = f1 | (f1(x1, noise1), y1_obs)
f2_post = f2 | (f2(x2, noise2), y2_obs)
# Predict first output.
mean1, lower1, upper1 = f1_post(x).marginal_credible_bounds()
# Predict second output with Monte Carlo.
samples = [
f2_post(B.stack(x, f1_post(x).sample()[:, 0], axis=1)).sample()[:, 0]
for _ in range(100)
]
mean2 = np.mean(samples, axis=0)
lower2 = np.percentile(samples, 2.5, axis=0)
upper2 = np.percentile(samples, 100 - 2.5, axis=0)
# Plot result.
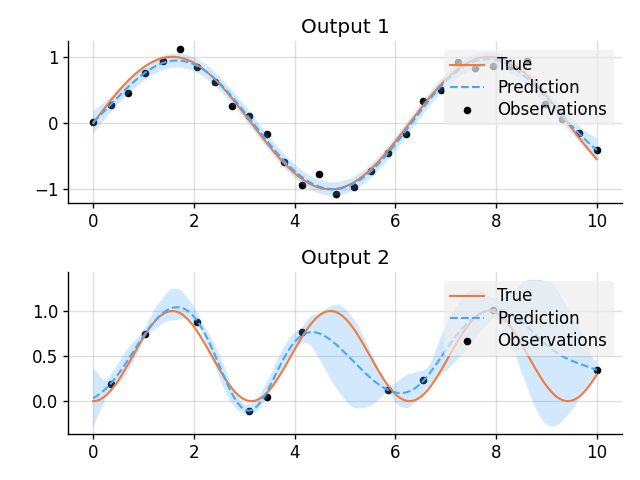
plt.figure()
plt.subplot(2, 1, 1)
plt.title("Output 1")
plt.plot(x, f1_true, label="True", style="test")
plt.scatter(x_obs1, y1_obs, label="Observations", style="train", s=20)
plt.plot(x, mean1, label="Prediction", style="pred")
plt.fill_between(x, lower1, upper1, style="pred")
tweak()
plt.subplot(2, 1, 2)
plt.title("Output 2")
plt.plot(x, f2_true, label="True", style="test")
plt.scatter(x_obs2, y2_obs, label="Observations", style="train", s=20)
plt.plot(x, mean2, label="Prediction", style="pred")
plt.fill_between(x, lower2, upper2, style="pred")
tweak()
plt.savefig("readme_example7_gpar.png")
plt.show()import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from varz.spec import parametrised, Positive
from varz.tensorflow import Vars, minimise_adam
from wbml.net import rnn as rnn_constructor
from wbml.plot import tweak
from stheno.tensorflow import B, Measure, GP, EQ
# Increase regularisation because we are dealing with `tf.float32`s.
B.epsilon = 1e-6
# Construct points which to predict at.
x = B.linspace(tf.float32, 0, 1, 100)[:, None]
inds_obs = B.range(0, int(0.75 * len(x))) # Train on the first 75% only.
x_obs = B.take(x, inds_obs)
# Construct function and observations.
# Draw random modulation functions.
a_true = GP(1e-2 * EQ().stretch(0.1))(x).sample()
b_true = GP(1e-2 * EQ().stretch(0.1))(x).sample()
# Construct the true, underlying function.
f_true = (1 + a_true) * B.sin(2 * np.pi * 7 * x) + b_true
# Add noise.
y_true = f_true + 0.1 * B.randn(*f_true.shape)
# Normalise and split.
f_true = (f_true - B.mean(y_true)) / B.std(y_true)
y_true = (y_true - B.mean(y_true)) / B.std(y_true)
y_obs = B.take(y_true, inds_obs)
@parametrised
def model(vs, a_scale: Positive = 0.1, b_scale: Positive = 0.1, noise: Positive = 0.01):
# Construct an RNN.
f_rnn = rnn_constructor(
output_size=1, widths=(10,), nonlinearity=B.tanh, final_dense=True
)
# Set the weights for the RNN.
num_weights = f_rnn.num_weights(input_size=1)
weights = Vars(tf.float32, source=vs.get(shape=(num_weights,), name="rnn"))
f_rnn.initialise(input_size=1, vs=weights)
with Measure():
# Construct GPs that modulate the RNN.
a = GP(1e-2 * EQ().stretch(a_scale))
b = GP(1e-2 * EQ().stretch(b_scale))
# GP-RNN model:
f_gp_rnn = (1 + a) * (lambda x: f_rnn(x)) + b
return f_rnn, f_gp_rnn, noise, a, b
def objective_rnn(vs):
f_rnn, _, _, _, _ = model(vs)
return B.mean((f_rnn(x_obs) - y_obs) ** 2)
def objective_gp_rnn(vs):
_, f_gp_rnn, noise, _, _ = model(vs)
evidence = f_gp_rnn(x_obs, noise).logpdf(y_obs)
return -evidence
# Pretrain the RNN.
vs = Vars(tf.float32)
minimise_adam(objective_rnn, vs, rate=5e-3, iters=1000, trace=True, jit=True)
# Jointly train the RNN and GPs.
minimise_adam(objective_gp_rnn, vs, rate=1e-3, iters=1000, trace=True, jit=True)
_, f_gp_rnn, noise, a, b = model(vs)
# Condition.
post = f_gp_rnn.measure | (f_gp_rnn(x_obs, noise), y_obs)
# Predict and plot results.
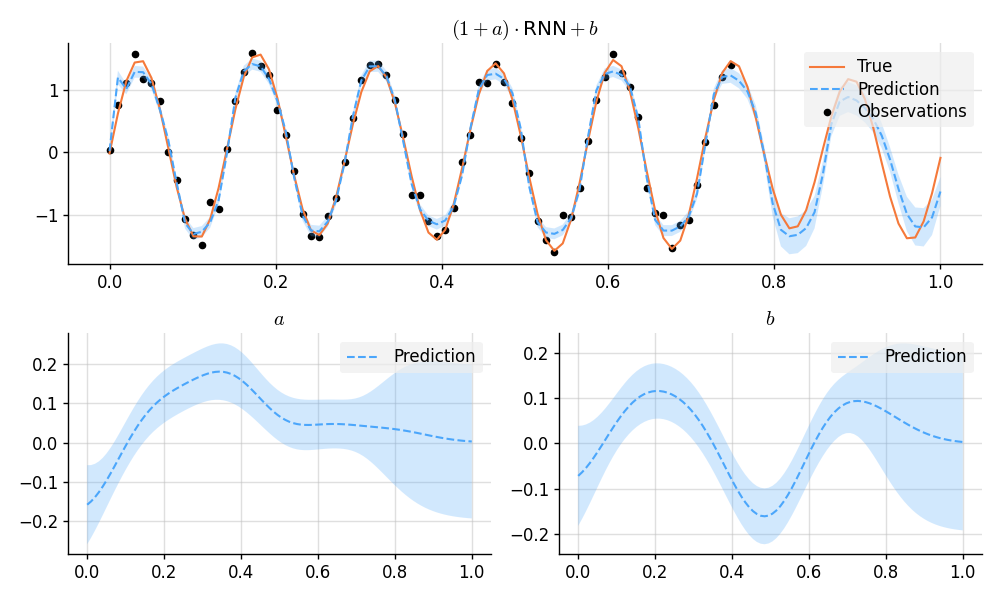
plt.figure(figsize=(10, 6))
plt.subplot(2, 1, 1)
plt.title("$(1 + a)\\cdot {}$RNN${} + b$")
plt.plot(x, f_true, label="True", style="test")
plt.scatter(x_obs, y_obs, label="Observations", style="train", s=20)
mean, lower, upper = post(f_gp_rnn(x)).marginal_credible_bounds()
plt.plot(x, mean, label="Prediction", style="pred")
plt.fill_between(x, lower, upper, style="pred")
tweak()
plt.subplot(2, 2, 3)
plt.title("$a$")
mean, lower, upper = post(a(x)).marginal_credible_bounds()
plt.plot(x, mean, label="Prediction", style="pred")
plt.fill_between(x, lower, upper, style="pred")
tweak()
plt.subplot(2, 2, 4)
plt.title("$b$")
mean, lower, upper = post(b(x)).marginal_credible_bounds()
plt.plot(x, mean, label="Prediction", style="pred")
plt.fill_between(x, lower, upper, style="pred")
tweak()
plt.savefig(f"readme_example8_gp-rnn.png")
plt.show()import matplotlib.pyplot as plt
from wbml.plot import tweak
from stheno import B, Measure, GP, EQ
# Define points to predict at.
x = B.linspace(0, 10, 100)
with Measure() as prior:
f1 = GP(3, EQ())
f2 = GP(3, EQ())
# Compute the approximate product.
f_prod = f1 * f2
# Sample two functions.
s1, s2 = prior.sample(f1(x), f2(x))
# Predict.
f_prod_post = f_prod | ((f1(x), s1), (f2(x), s2))
mean, lower, upper = f_prod_post(x).marginal_credible_bounds()
# Plot result.
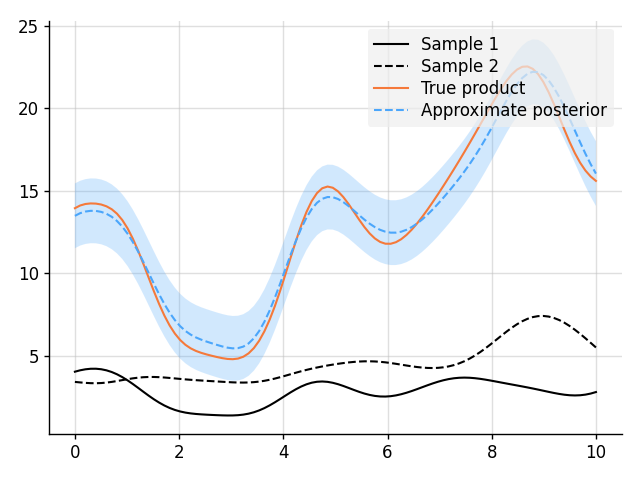
plt.plot(x, s1, label="Sample 1", style="train")
plt.plot(x, s2, label="Sample 2", style="train", ls="--")
plt.plot(x, s1 * s2, label="True product", style="test")
plt.plot(x, mean, label="Approximate posterior", style="pred")
plt.fill_between(x, lower, upper, style="pred")
tweak()
plt.savefig("readme_example9_product.png")
plt.show()import matplotlib.pyplot as plt
import wbml.out as out
from wbml.plot import tweak
from stheno import B, GP, EQ, PseudoObs
# Define points to predict at.
x = B.linspace(0, 10, 100)
x_obs = B.linspace(0, 7, 50_000)
x_ind = B.linspace(0, 10, 20)
# Construct a prior.
f = GP(EQ().periodic(2 * B.pi))
# Sample a true, underlying function and observations.
f_true = B.sin(x)
y_obs = B.sin(x_obs) + B.sqrt(0.5) * B.randn(*x_obs.shape)
# Compute a pseudo-point approximation of the posterior.
obs = PseudoObs(f(x_ind), (f(x_obs, 0.5), y_obs))
# Compute the ELBO.
out.kv("ELBO", obs.elbo(f.measure))
# Compute the approximate posterior.
f_post = f | obs
# Make predictions with the approximate posterior.
mean, lower, upper = f_post(x).marginal_credible_bounds()
# Plot result.
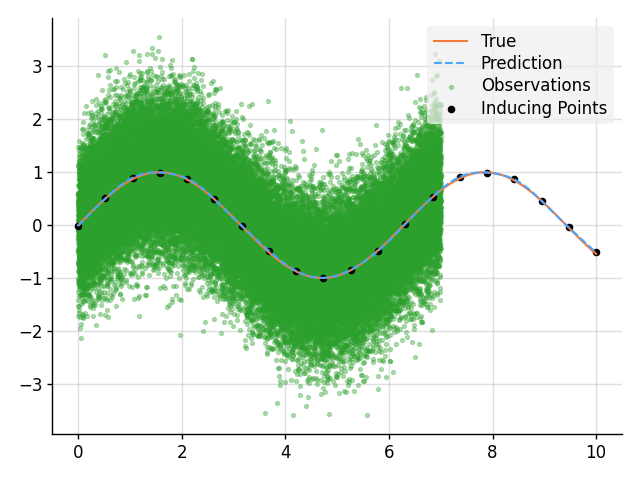
plt.plot(x, f_true, label="True", style="test")
plt.scatter(
x_obs,
y_obs,
label="Observations",
style="train",
c="tab:green",
alpha=0.35,
)
plt.scatter(
x_ind,
obs.mu(f.measure)[:, 0],
label="Inducing Points",
style="train",
s=20,
)
plt.plot(x, mean, label="Prediction", style="pred")
plt.fill_between(x, lower, upper, style="pred")
tweak()
plt.savefig("readme_example10_sparse.png")
plt.show()import matplotlib.pyplot as plt
from wbml.plot import tweak
from stheno import B, Measure, GP, EQ
# Define points to predict at.
x = B.linspace(0, 10, 100)
x_obs = B.linspace(0, 10, 20)
with Measure() as prior:
w = lambda x: B.exp(-(x**2) / 0.5) # Basis function
b = [(w * GP(EQ())).shift(xi) for xi in x_obs] # Weighted basis functions
f = sum(b)
# Sample a true, underlying function and observations.
f_true, y_obs = prior.sample(f(x), f(x_obs, 0.2))
# Condition on the observations to make predictions.
post = prior | (f(x_obs, 0.2), y_obs)
# Plot result.
for i, bi in enumerate(b):
mean, lower, upper = post(bi(x)).marginal_credible_bounds()
kw_args = {"label": "Basis functions"} if i == 0 else {}
plt.plot(x, mean, style="pred2", **kw_args)
plt.plot(x, f_true, label="True", style="test")
plt.scatter(x_obs, y_obs, label="Observations", style="train", s=20)
mean, lower, upper = post(f(x)).marginal_credible_bounds()
plt.plot(x, mean, label="Prediction", style="pred")
plt.fill_between(x, lower, upper, style="pred")
tweak()
plt.savefig("readme_example11_nonparametric_basis.png")
plt.show()