-
Notifications
You must be signed in to change notification settings - Fork 10
Home
Generates monocrystal in PBC (but the description below is also relevant to generating bicrystals.)
Out of box supports Fe (bcc), Cu (fcc), NaCl, Si and diamond (both have the diamond structure), SiC (zinc blende, wurtzite or any polytype specified by a sequence of letters). Other systems can be easily added in the get_named_lattice() function.
Update 2018: it is now possible to use cif files (for example, from COD)
to describe structure. For this you need to install Gemmi for your Python
(pip install gemmi), get a cif file and use its path as the first parameter (monocryst.py ~/Downloads/1010995.cif 2 2 3 output2.cfg).
Generate Si crystal with the size equal or larger than 2nm x 2nm x 3nm:
monocryst.py si 2 2 3 output.cfg
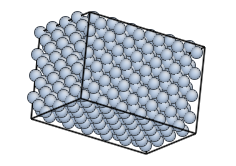
Option --margin generates a cuboid in PBC, by padding the monocrystal with vacuum (of course it's not a monocrystal anymore):
monocryst.py --margin=1 NaCl 4 4 4 nacl.cfg
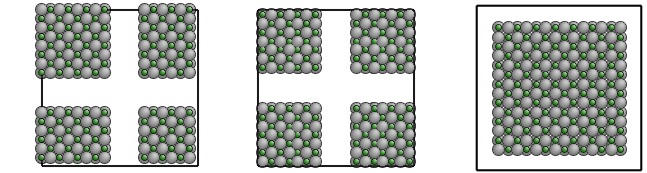
All the three pictures present the same configuration, shifted under PBC.
The command above generates the system in the left picture.
With the additional --center-zero option, the center of the configuration is exactly at (0,0,0),
like in the middle picture.
In AtomEye program, it is possible to shift the view under PBC, using mouse.
If your visualization program cannot do this and you want to see the cube in one piece,
you may use a program from the debyer toolset:
# shift the system by half of the PBC in x, y and z directions.
dbr_extend -r -S0.5,0.5,0.5 -i nacl.cfg
Having a configuration with the center at or near (0,0,0) makes mathematic calculations easier. For example, command
mdfile.py --prefer-negative --filter='abs(x)+abs(y)+abs(z) < 20' nacl.cfg nacl-oct.cfg
makes octahedron. The --prefer-negative option changes the internal processing of the coordinates:
they are mapped to the (-H/2, H/2) range, instead of (0, H), where H is the PBC box size.
Info about coincident site lattice (CSL) grain boundaries in cubic crystals. Shows usage instructions when called without arguments.
Example. Print angle of rotation for Σ=5 grain boundary with the [001] axis of rotation:
$ ./csl.py 001 5
m= 3 n= 1 36.870
m= 2 n= 1 53.130
m= 1 n= 2 126.870
m= 1 n= 3 143.130
Generates bicrystals (more precisely, models of bicrystals, a starting point for getting more realistic models). This script has been used to generate only symmetric tilt and twist GBs in cubic systems. Nonetheless, it has a lot of options. Running the script without any parameters prints help (but the help is not complete).
Generate diamond bicrystal:
- rotation axis [100],
- median plane (011), i.e. its a tilt boundary,
- Σ=13 (pick the lowest rotation angle for Σ=13),
- min. dimensions: 0.8 x 0.8 x 3 nm,
- do not adjust z dimension
- add 1.0nm vacuum in z dimension
- if two atoms are in a distance smaller than 0.5, remove one of them
bicrystal.py 100 m011 13 0.8 0.8 3 nozfit remove:0.5 vacuum:1.0 lattice:diamond d13-ini.cfg
The GB is constructed at the z=0 plane, so you may want to shift it under PBC before visualization, like in the nacl.cfg case above.
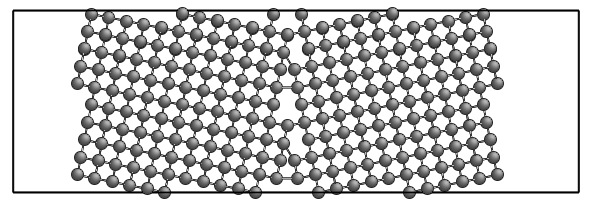
Let's now try to construct <110> symmetric tilt grain boundaries in Cu, similar to that in the paper: M. Tschopp et al., Acta Materialia 55 (2007) 3959-3969. Let's pick Σ267 (11,11,5) θ=144.4° boundary (Fig. 3f). To learn more about <110> Σ267 GBs, use csl.py:
$ ./csl.py 110 267
m=22 n= 5 35.636
m=13 n= 7 74.579
m=14 n=13 105.421
m= 5 n=11 144.364
The m and n integers are used to generate boundaries (see Grimmer, Acta Cryst. (1984) A40, 108). m,n can be used as a bicrystal.py parameter, instead of the Σ.
In this case: 5,11.
If the rotation axis is [110], the (11,11,5) plane does not contain the axis, so to have tilt boundary, we use the equivalent (11,-11,5) plane.
The final command is
./bicrystal.py 1,1,0 11,-11,5 5,11 2 2 3 lattice:cu out.cfg
And we got GB with the 5 macroscopic degrees of freedom the same as in the Fig. 3f.

The system is periodic and there are two GBs. To get only one GB use the vacuum option, as in the previous example.
As you can see, in this geometrical construction some GB atoms are very close to each other. This system is clearly not a realistic model of the GB. The remove option (see the previous example) can remove the atoms that are too close to each other, but this is only the first step (and this step may not be necessary) to create more realistic models.
For crystals defined in monomers.py, such as SiC or NaCl, atoms removal preserves stoichiometry -- Na is removed together with Cl. If the crystal description comes from a CIF file, each atom is evaluated separately.
The complete procedure that we used to prepare GBs is described in the paper:
M. Wojdyr et al, Energetics and structure of <001> tilt grain boundaries in SiC,
Modelling Simul. Mater. Sci. Eng. 18 075009 (2010)
(free preprint).
bicrystal.py was written on that occasion, but I've heard from a few other people
that used or tried to use it in their research.
Manipulates coordinate files and converts between file formats. Can handle gzipped (.gz) and bzip2'ed (.bz2) files. See the list of the supported files in the source.
Convert VASP POSCAR file to LAMMPS input.
mdfile.py POSCAR foo.lammps
Convert all AtomEye cfg files to gzipped input LAMMPS files.
bash$ for i in *.cfg; do ../../mdfile.py $i `basename $i .cfg`.lammps.gz; done
Change all atoms B to C and Cl to Si.
mdfile.py --translate 'B->C, Cl->Si' input.cfg output.cfg
Swap Si and C atoms.
mdfile.py --translate 'Si->C, C->Si' input.cfg output.cfg
Set explicitly PBC box size.
mdfile.py --pbc '[(60,0,0),(0,60,0),(0,0,60)]' input.xyz output.cfg
Remove atoms that have the z coordinate outside of the (15,30) range.
mdfile.py --filter '15 < z < 30' input.cfg output.cfg
In addition to Python and Numpy, graingen.py it requires qhull.
On Linux install a package such as qhull (Fedora) or qhull-bin (Ubuntu).
On Windows download and put qhull.exe in the gosam directory.
graingen.py generates crystalline grains. It is recommended to use it from a python script that looks like a configuration file, but has imports at the beginning and a call to generate_grain() at the end.
Example 1. Let's create a file Fe_r4.py:
from graingen import *
cell = CubicUnitCell(a=2.87)
atoms = [
("Fe", 0.0, 0.0, 0.0),
("Fe", 0.5, 0.5, 0.5),
]
surfaces = LatticeSurface(r=4)
generate_grain(globals())
Put this file in the gosam directory.
On Windows: click the script to execute it.
On Unix system: type
$ python Fe_r4.py
The script should produce two files with the same basename: log file Fe_r4.log and output configuration Fe_r4.xyz.
The import statement above, in the first line of the script, works
if your script is in the same directory as the graingen.py file.
Alternatively, you may install gosam as Python package and use:
from gosam.graingen import *
Assignment of the cell variable defines unit cell. Usually values in ångströms are used, but the program is unit agnostic. Any unit can be used (consistently). The coordinates in the output file will be in the same unit that was used in the configuration file.
Assignment of the atoms variable defines positions of atoms in the unit cell.
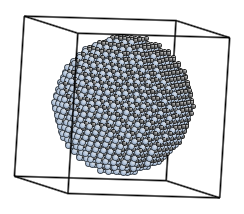
The surfaces variable is responsible for size and shape of the grain. In the example above, the surface is spherical and the radius is 4Å.
The script above generates bcc lattice and cuts out an atomic cluster discarding atoms outside of the r=4Å sphere.
Instead of the sphere, one can use a convex polyhedron defined by a set of planes:
surfaces = [
# each plane is defined by Miller indices and distance r from (0,0,0)
LatticeSurface( hkl=(0,-1,0), r=25 ),
LatticeSurface( hkl=(-1,0,0), r=25 ),
# ...
# polyhedron needs at least 4 planes
]
It is possible to define surface deformation (the relaxation of atoms at the surface). The deformation can be defined as displacement of atoms from the perfect lattice positions, in direction normal to the surface, with displacement magnitude given as a function of the distance from the surface. For example:
LatticeSurface.default_sd = SurfaceDeformation(depth=8.3,
fun=lambda x: (8.3-x)*0.05 )
To assign different deformation for each surface plane define LatticeSurface with parameter sd, like this:
def func(d):
return 0.02 * (10-d)**2
surfaces = [
LatticeSurface( hkl=(1,0,0), r=5 ),
LatticeSurface( hkl=(-1,0,0), r=5 ),
LatticeSurface( hkl=(0,1,0), r=10 ),
LatticeSurface( hkl=(0,-1,0), r=10 ),
LatticeSurface( hkl=(0,0,1), r=15, sd=SurfaceDeformation(10, func) ),
LatticeSurface( hkl=(0,0,-1), r=15 ),
]
If the function named modifier is defined, it is used to modify each atom.
This can be used to add thermal vibrations:
def modifier(atom):
sigma = 0.025
atom.pos += (random.gauss(0, sigma),
random.gauss(0, sigma),
random.gauss(0, sigma))
Each atom has three properties:
-
name-- atomic symbol -
pos-- position (x, y, z) in ångströms -
min_dist-- distance to the grain surface It is possible to specify different vibrations for atoms near the surface, or different vibrations for different atomic species.
It is possible to generate vacancies (remove some atoms) by specifying the probability of vacancy:
vacancy_probability = 0.01
Different species can have different probabilities:
vacancy_probability = { "Si": 0.01, "C": 0.02 }
The vacancy_probability variable can be defined as a function that takes atom and returns probability:
def vacancy_probability(atom):
if atom.min_dist < 5: # surface, 5A shell
return 0.05
else # core
return 0.01
The modifier() function can be used to add substitutional impurity atoms:
# this substitutes, with 2% probability, any atoms with oxygen
def modifier(atom):
if random.random() < 0.02:
atom.name = "O"
Note that if you already have the modifier() function in your file, you need to add code to that function. Do not create two functions with the same name.
Instead of atoms, as in the first example, two variables: nodes and node_atoms can be used.
nodes = [
(0.0, 0.0, 0.0),
(0.5, 0.5, 0.0),
(0.0, 0.5, 0.5),
(0.5, 0.0, 0.5),
]
node_atoms = [
("Si", 0.0, 0.0, 0.0),
("C", 0.25,0.25,0.25),
]
There are two predefined lists of nodes: fcc_nodes and bcc_nodes. This is equivalent to the assignment in the example above:
nodes = fcc_nodes
If the unit cell has n nodes and m node atoms, it has n × m atoms. The positions in the second list are added to the node position.
Nodes contain one or more atoms that are, by default, kept together. To ungroup nodes, add line:
do_not_group_nodes=True
The output_file variable sets the basename of log file and output files.
If not set, the basename is set to the basename of the script.
output_file = "foo"
The output_formats variable contains a list of output formats. It should contain one or more formats supported by mdfile.py (XYZ, AtomEye, LAMMPS and others).
output_formats = ["xyz"]
output_formats = ["xyz", "atomeye"]
Additionally, a log of the operation is written to a file with the .log extension.
More complex example that generates a spherical grain of cubic SiC:
#!/usr/bin/env python
import random
from graingen import *
output_file = "cub_sic"
output_formats = ["atomeye"]
cell = CubicUnitCell(4.36)
#nodes in unit cell (as fraction of unit cell parameters)
nodes = [
(0.0, 0.0, 0.0),
(0.5, 0.5, 0.0),
(0.0, 0.5, 0.5),
(0.5, 0.0, 0.5),
]
# alternatively, predefined lists fcc_nodes and bcc_nodes can be used, e.g:
#nodes = fcc_nodes
#atoms in node (as fraction of unit cell parameters)
node_atoms = [
("Si", 0.0, 0.0, 0.0),
("C", 0.25,0.25,0.25),
]
# the simplest case - spherical grain
surfaces = LatticeSurface(r=25)
# add thermal vibrations
def modifier(atom):
sigma = 0.025
atom.pos += (random.gauss(0, sigma),
random.gauss(0, sigma),
random.gauss(0, sigma))
#vacancy_probability = { "Si": 0.01, "C": 0.02 }
generate_grain(globals())