README_EN.md

1824. Minimum Sideway Jumps

中文文档

Description

There is a 3 lane road of length n that consists of n + 1 points labeled from 0 to n. A frog starts at point 0 in the second lane and wants to jump to point n. However, there could be obstacles along the way.

You are given an array obstacles of length n + 1 where each obstacles[i] (ranging from 0 to 3) describes an obstacle on the lane obstacles[i] at point i. If obstacles[i] == 0, there are no obstacles at point i. There will be at most one obstacle in the 3 lanes at each point.

• For example, if obstacles[2] == 1, then there is an obstacle on lane 1 at point 2.

The frog can only travel from point i to point i + 1 on the same lane if there is not an obstacle on the lane at point i + 1. To avoid obstacles, the frog can also perform a side jump to jump to another lane (even if they are not adjacent) at the same point if there is no obstacle on the new lane.

• For example, the frog can jump from lane 3 at point 3 to lane 1 at point 3.

Return the minimum number of side jumps the frog needs to reach any lane at point n starting from lane 2 at point 0.

Note: There will be no obstacles on points 0 and n.

 

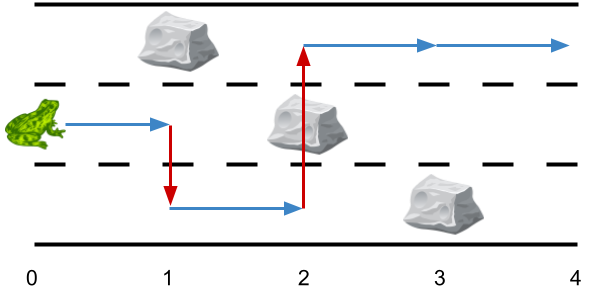
Example 1:

Input: obstacles = [0,1,2,3,0]
Output: 2 
Explanation: The optimal solution is shown by the arrows above. There are 2 side jumps (red arrows).
Note that the frog can jump over obstacles only when making side jumps (as shown at point 2).

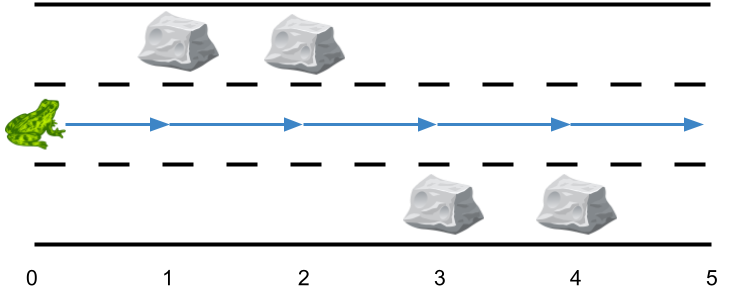
Example 2:

Input: obstacles = [0,1,1,3,3,0]
Output: 0
Explanation: There are no obstacles on lane 2. No side jumps are required.

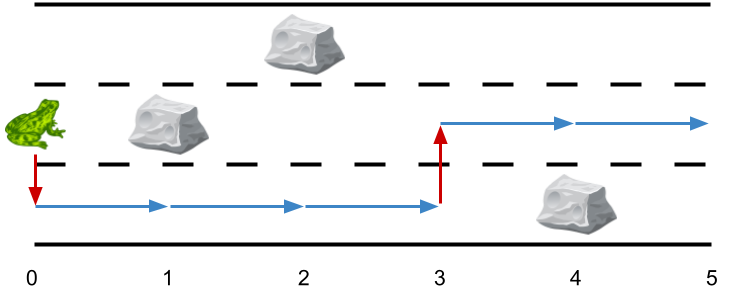
Example 3:

Input: obstacles = [0,2,1,0,3,0]
Output: 2
Explanation: The optimal solution is shown by the arrows above. There are 2 side jumps.

 

Constraints:

• obstacles.length == n + 1
• 1 <= n <= 5 * 105
• 0 <= obstacles[i] <= 3
• obstacles[0] == obstacles[n] == 0

Solutions

Python3

class Solution:
    def minSideJumps(self, obstacles: List[int]) -> int:
        f = [1, 0, 1]
        for v in obstacles[1:]:
            g = [inf] * 3
            for j in range(3):
                if v != j + 1:
                    g[j] = f[j]
            if v != 1:
                g[0] = min(g[0], min(g[1], g[2]) + 1)
            if v != 2:
                g[1] = min(g[1], min(g[0], g[2]) + 1)
            if v != 3:
                g[2] = min(g[2], min(g[0], g[1]) + 1)
            f = g
        return min(f)

Java

class Solution {
    private int inf = 0x3f3f3f3f;

    public int minSideJumps(int[] obstacles) {
        int[] f = new int[] {1, 0, 1};
        for (int i = 1; i < obstacles.length; ++i) {
            int v = obstacles[i];
            int[] g = new int[] {inf, inf, inf};
            for (int j = 0; j < 3; ++j) {
                if (v != j + 1) {
                    g[j] = f[j];
                }
            }
            if (v != 1) {
                g[0] = Math.min(g[0], Math.min(g[1], g[2]) + 1);
            }
            if (v != 2) {
                g[1] = Math.min(g[1], Math.min(g[0], g[2]) + 1);
            }
            if (v != 3) {
                g[2] = Math.min(g[2], Math.min(g[0], g[1]) + 1);
            }
            f = g;
        }
        return Math.min(f[0], Math.min(f[1], f[2]));
    }
}

C++

class Solution {
public:
    const int inf = 0x3f3f3f3f;

    int minSideJumps(vector<int>& obstacles) {
        vector<int> f = {1, 0, 1};
        for (int i = 1; i < obstacles.size(); ++i) {
            int v = obstacles[i];
            vector<int> g(3, inf);
            for (int j = 0; j < 3; ++j) if (v != j + 1) g[j] = f[j];
            if (v != 1) g[0] = min(g[0], min(g[1], g[2]) + 1);
            if (v != 2) g[1] = min(g[1], min(g[0], g[2]) + 1);
            if (v != 3) g[2] = min(g[2], min(g[0], g[1]) + 1);
            f = move(g);
        }
        return *min_element(f.begin(), f.end());
    }
};

Go

func minSideJumps(obstacles []int) int {
	inf := 0x3f3f3f3f
	f := [3]int{1, 0, 1}
	for _, v := range obstacles[1:] {
		g := [3]int{inf, inf, inf}
		for j := 0; j < 3; j++ {
			if v != j+1 {
				g[j] = f[j]
			}
		}
		if v != 1 {
			g[0] = min(g[0], min(g[1], g[2])+1)
		}
		if v != 2 {
			g[1] = min(g[1], min(g[0], g[2])+1)
		}
		if v != 3 {
			g[2] = min(g[2], min(g[0], g[1])+1)
		}
		f = g
	}
	return min(f[0], min(f[1], f[2]))
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

...