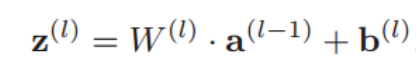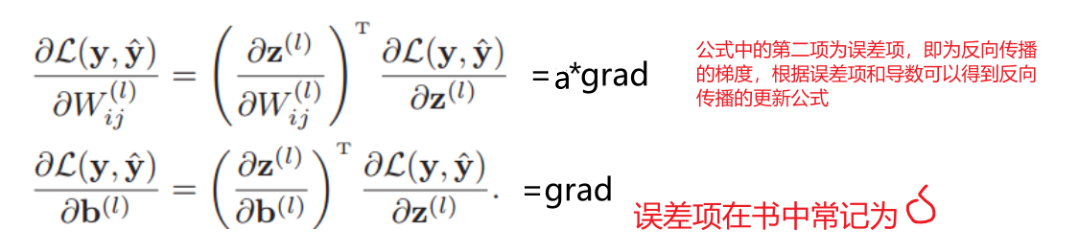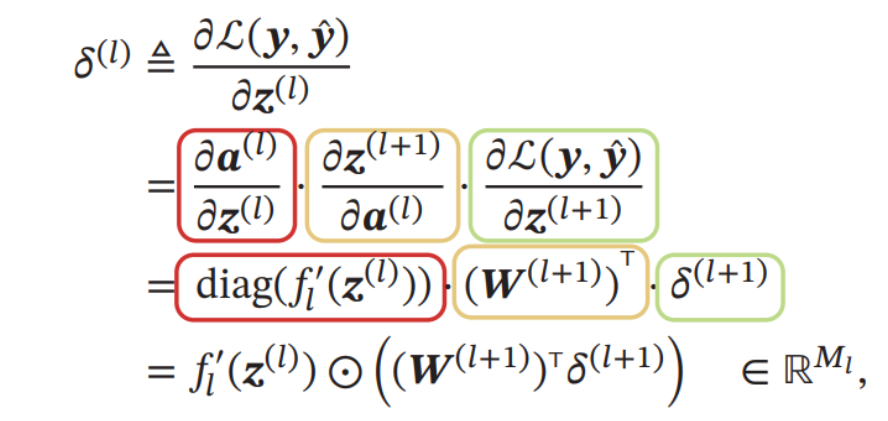实验 用numpy搭建全连接神经网络用于手写数字识别

结合代码和公式对全连接神经网络的实现进行分析

数据处理

# 标准化处理  
if normalize:  
    for _ in ('train_img', 'test_img'):  
        dataset[_] = dataset[_].astype(np.float32) / 255.0  
# one_hot_label处理  
if one_hot_label:  
    for _ in ('train_label', 'test_label'):  
        t = np.zeros((dataset[_].size, 10))  
        for idx, row in enumerate(t):  
            row[dataset[_][idx]] = 1  
        dataset[_] = t  
# 展平处理  
if flatten:  
    for _ in ('train_img', 'test_img'):  
        dataset[_] = dataset[_].reshape(-1, 784)  
# 划分验证集  
if val_data:  
    x_val_data, x_test_data = np.split(dataset['test_img'], 2)  
    y_val_data, y_test_data = np.split(dataset['test_label'], 2)  
    return dataset['train_img'], dataset['train_label'], x_val_data, y_val_data, x_test_data, y_test_data

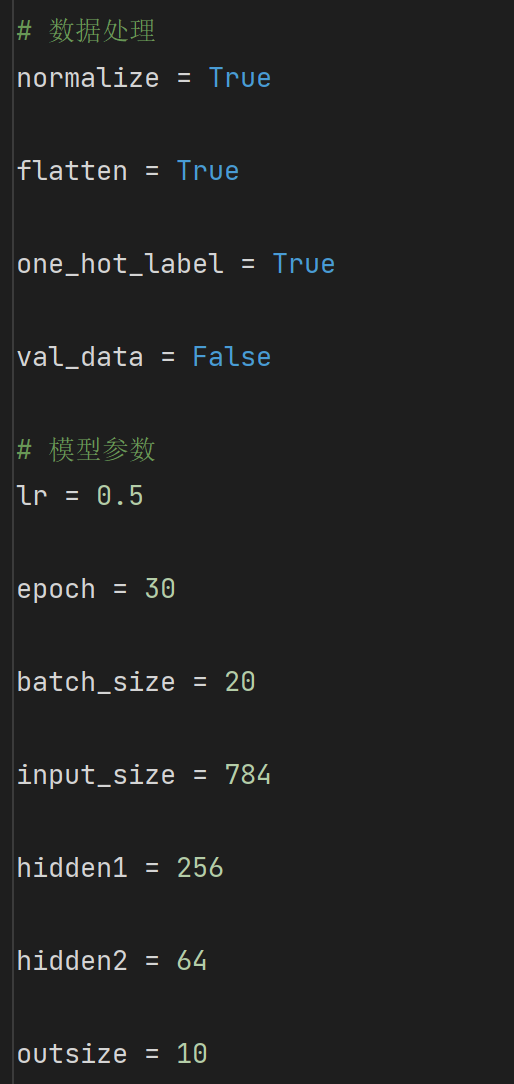
• 标准化处理：将数据归一化

• one hot处理：将数据处理成one hot形式，即维度扩充为与数据类别相同，数据为哪个类别，其相应维度上的值为1，否则为0

• 展平处理：将28*28的图像转换成一个维度上784的大小

• 划分验证集：原数据集为训练集：测试集60000：10000，把测试集中的5000条作为验证集

全连接层

class Net(object):  
    def __init__(self, num_input, num_output):  
        self.num_input = num_input  
        self.num_output = num_output  
        self.w = np.random.normal(loc=0.0, scale=0.01, size=(self.num_input, self.num_output))  # 随机初始化参数 假设为(n, m)  
        self.bias = np.zeros([1, self.num_output])  # 初始化为0  (1, m)  
        self.input_data = np.zeros(0)  
        self.output_data = np.zeros(0)  
        self.grad_w = np.zeros(0)  
        self.grad_b = np.zeros(0)  
  
    def forward(self, input_data):  
        self.input_data = input_data  # 假设input_data = (1, n)  
        self.output_data = np.matmul(self.input_data, self.w) + self.bias  # (1, n) * (n, m) = (1, m) m为下一层的输入维度  
        return self.output_data  
  
    def backward(self, grad):  
        self.grad_w = np.dot(self.input_data.T, grad)  # (n, 1) * (1, m) = (n, m)  
        self.grad_b = np.sum(grad, axis=0)  
        next_grad = np.dot(grad, self.w.T)  # (1, m) * (m, n) = (1, n)  
        return next_grad  
  
    def backward_with_l2(self, grad, lamb, batch_size):  
        self.grad_w = np.dot(self.input_data.T, grad) + (lamb / batch_size) * self.w  
        self.grad_b = np.sum(grad, axis=0)  
        next_grad = np.dot(grad, self.w.T)  
        return next_grad  
  
    def update(self, lr):  
        self.w = self.w - lr * self.grad_w  
        self.bias = self.bias - lr * self.grad_b

定义一个类，在其中实现的功能有：

• 初始化：在创建一层全连接层时，需要初始化w和b，w为（m，n）其中m为输入数据的维度，n为下一层的输入维度，b为（1，n）.公式如下:

• 前馈函数：在前馈函数中实现上面的公式

• 反向传播：需要根据损失更新参数w和b的值，因此分别对w和b求偏导

前一层的梯度可以根据后一层的梯度得到: 根据上面这个公式，可以发现，前一层可以使用后一层的误差项来得到自己的误差项，而不需要从最后用链式法则进行推导。因此称为反向传播。 推导过程如下：

• 更新参数：在原来的参数上减去梯度方向得到新的参数，实验中往往需要学习率来控制更新的程度

激活函数

class ReLU(object):  
  
    def __init__(self):  
        self.input_data = np.zeros(0)  
  
    def forward(self, input_data):  
        self.input_data = input_data  
        output_data = np.maximum(0, input_data)  # (1, n)  
        return output_data  
  
    def backward(self, grad):  
        next_grad = grad  # (1, n) * (1, n) 逐元素相乘  
        next_grad[self.input_data < 0] = 0  
        return next_grad

激活函数同样需要两个，一个实现前向传播，一个实现反向传播

Softmax+交叉熵损失

class Softmax(object):  
    def __init__(self):  
        self.prob = np.zeros(0)  
        self.batch_size = []  
        self.label = []  
  
    def forward(self, input_data):  
        input_max = np.max(input_data, axis=1, keepdims=True)  
        input_exp = np.exp(input_data - input_max)  
        self.prob = input_exp / np.sum(input_exp, axis=1, keepdims=True)  
        return self.prob  
  
    def get_loss(self, label):  # 计算损失  
        self.label = label  
        self.batch_size = self.prob.shape[0]  
        loss = -np.sum(label * np.log(self.prob + 1e-7)) / self.batch_size  
        return loss  
  
    def backward(self):  
        grad = (self.prob - self.label) / self.batch_size  
        return grad

在Softmax中除了实现前向和后向传播外，添加了用交叉熵计算损失的函数，这是因为在softmax后加交叉熵，反向传播的公式会更简便。

MSE损失（Mean squared error均方误差）

def MSE_loss(self, y_pre, y):  
    loss = 0.5 * np.sum((y_pre - y) ** 2) / batch_size  
    grad = (y_pre - y) / batch_size  
    return loss, grad

整体的传播

def forward(self, input_data):  # 神经网络的前向传播  
    h1 = self.fc1.forward(input_data)  
    h1 = self.relu1.forward(h1)  
    # h1 = self.sigmoid1.forward(h1)  
    h2 = self.fc2.forward(h1)  
    h2 = self.relu2.forward(h2)  
    # h2 = self.sigmoid2.forward(h2)  
    h3 = self.fc3.forward(h2)  
    # prob = self.softmax.forward(h1)  
    return h3  
  
def backward(self, y_pre, y):  # 神经网络的反向传播  
    _, grad = self.MSE_loss(y_pre, y)  
    # grad = self.softmax.backward()  
    dh3 = self.fc3.backward(grad)  
    dh2 = self.relu2.backward(dh3)  
    # dh2 = self.sigmoid2.backward(dh3)  
    dh2 = self.fc2.backward(dh2)  
    dh1 = self.relu1.backward(dh2)  
    # dh1 = self.sigmoid1.backward(dh2)  
    dh1 = self.fc1.backward(dh1)
    
def update(self, lr):  
    self.fc1.update(lr)  
    self.fc2.update(lr)  
    self.fc3.update(lr)

实验结果

使用mini-batch GD，使用效果较好的模型参数

得到实验结果如下：

最终测试集准确率稳定在98%以上。