3edu03

예제

[01] 선형회귀를 이용한 광고에 소요되는 비용으로 클릭수 예측하기

1. Data

   /ws_python/notebook/machine/basic/click.csv

   • x: 광고 비용, y: 클릭수

   x,y
   235,591
   216,539
   148,413
   35,310
   85,308
   204,519
   49,325
   25,332
   173,498
   191,498
   134,392
   99,334
   117,385
   112,387
   162,425
   272,659
   159,400
   159,427
   59,319
   198,522
   

2. Script

   /ws_python/notebook/machine/basic/Regression1.ipynb

   import pandas as pd
   import numpy as np
   import matplotlib
   import matplotlib.pyplot as plt
   from matplotlib import font_manager, rc
   
   font_name = font_manager.FontProperties(fname="C:/Windows/Fonts/malgun.ttf").get_name()
   # windows 10
   # font_name = font_manager.FontProperties(fname="C:/Windows/Fonts/malgunsl.ttf").get_name()
   rc('font', family=font_name)           # 맑은 고딕 폰트 지정
   plt.rcParams["font.size"] = 12         # 글자 크기
   # plt.rcParams["figure.figsize"] = (10, 4) # 10:4의 그래프 비율
   plt.rcParams['axes.unicode_minus'] = False  # minus 부호는 unicode 적용시 한글이 깨짐으로 설정
   
   # Jupyter에게 matplotlib 그래프를 출력 영역에 표시할 것을 지시하는 명령
   %matplotlib inline  

   # skiprows=1: 첫번재 행 skip
   train = np.loadtxt('click.csv', delimiter=',', dtype='int', skiprows=1)
   print(type(train)) # <class 'numpy.ndarray'>
   train_x = train[:, 0] # 모든행 0열
   train_y = train[:, 1] # 모든행 1열
   
   plt.plot(train_x, train_y, 'o')
   plt.show()

   a = a - ETA * np.sum(((f(train_z) - train_y) * train_z))  # 기울기
   print('a: {0}'.format(ETA * np.sum(((f(train_z) - train_y) * train_z))))
   b = b - ETA * np.sum(f(train_z) - train_y) # 편향, b - ETA * (ax + b의 값 - 실제값)
   print('b: {0}'.format(ETA * np.sum(f(train_z) - train_y)))

[참고] 표준정규분포(Standard Normal Distribution)

1. 표준정규분포

   • 평균과 분산이 다른 정규분포를 표준화한 것이 표준정규분포이다.
   • 표준정규분포는 정규분포의 근간이 되는 [평균 0과 표준편차를 1]로 고정하는 과정을 의미한다.
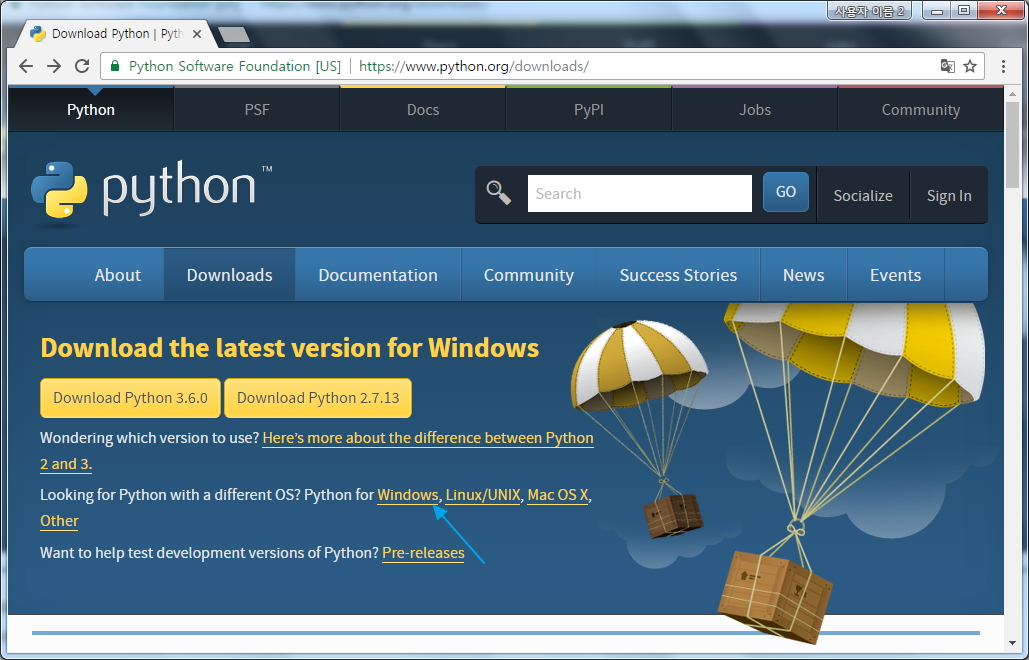
   • 정규분포의 확률(신뢰구간)을 구할 때 이용함.
   • 표준화 예(TOEIC <-> TOFEL <-> TEPS 점수 인정 비교)

2. 표준화 변수 Z

   • 정규분포의 확률변수 X를 구하기 위해서 표준정규분포로 바꾸는 변수를 표준화 변수 Z라고한다.
   • 정규분포를 표준정규분포로 바꾸는 Z의 공식 Z = X-μ / σ (X: 확률변수, μ: 평균, σ: 표준 편차)

   예) A 고등학교의 B반 학생의 국어 점수가 평균 75점, 표준편차 5점인 정규분포로 나타났다. 이 경우에 어느 학생의 점수가 70점~80점 사이일 확률은?

   평균: 75점, 표준 편차: 5점, 확률 변수: 70, 80

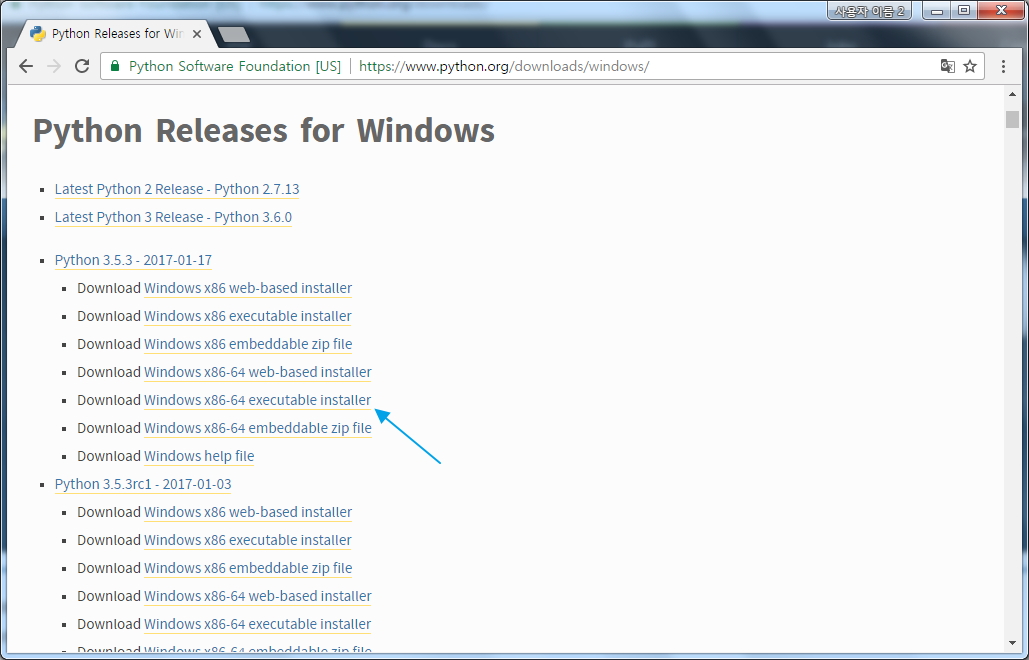
   z = 70 - 75 / 5 = -1, z = 80 - 75 / 5 = 1

   확률 구간 P(70 < X < 80) => P(Z=70 - 75 / 5 < Z < Z=80 - 75 / 5) = P(-1 < Z < 1) = P(-0.3413 < Z < +0.3413) = P(-34% < Z < + 34%) = 어느 학생의 점수가 70점~80점 사이일 확률은 68%이다.

   • Z값에 의해서 평균 0을 기준으로 ±1σ(표준편차)의 표준정규분포로 나타낸 경우

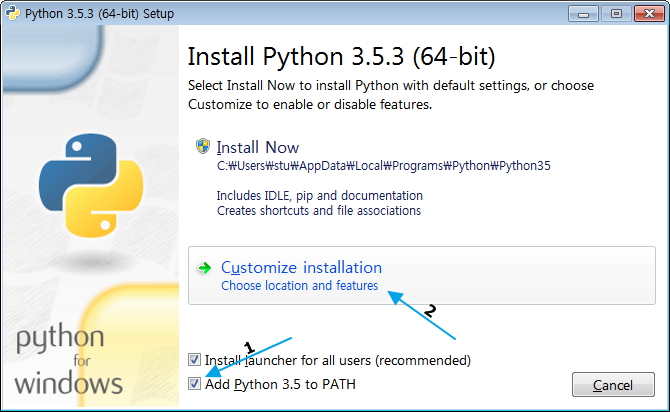
   예) A 고등학교의 B반 학생의 국어 점수가 평균 75점, 표준편차 5점인 정규분포로 나타났다. 이 경우에 어느 학생의 점수가 60점~90점 사이일 확률은?

   z = 60 - 75 / 5 = -3, z = 90 - 75 / 5 = 3

   확률 구간 P(60 < X < 90) => P(Z=60 - 75 / 5 < Z < Z=90 - 75 / 5) = P(-3 < Z < 3) = P(-0.4987 < Z < +0.4987) = P(-49% < Z < + 49%) = 어느 학생의 점수가 60점~90점 사이일 확률은 98%이다.