List of scheduling environments

Introduction

In the next sections, the scheduling models (layouts) currently implemented in scheptk is listed. The creation and usage of customised scheduling models is discussed here. The standard scheduling models implemented in scheptk are the following:

• Single Machine (SingleMachine class)
• Parallel Machines (ParalleMachines class)
• Unrelated Machines (UnrelatedMachines class)
• Flow Shop (FlowShop class)
• Job Shop (JobShop class)
• Open Shop (OpenShop class)

Single Machine

The SingleMachine class serves to model a single machine scheduling problem, where a set of jobs have to be processed on a single machine. This is the Gantt chart produced with the instance in the file and the solution procedure in the sample.

Attributes

Some of the Attributes are mandatory and produce an error if not found when loading the instance file. Others are optional, but they may produce errors in some cases if missing (e.g. if due dates are ommitted, then due-date related criteria cannot be computed).

• Mandatory:

• jobs - number of jobs
• pt - processing times (a list containing the processing time of each job)

• Optional:

• w - weights. The weight of each job. If not specified, they are assumed to be 1.0
• r - release dates. The earliest starting time of each job. If not specified, they are assumed to be 0
• dd - due dates. The due date of each job. If not specified, they are assumed to be infinite

Instance

A typical instance is the following:

[PT=2,10,1,1]
[DD=11,13,13,14]
[W=2.0,1,1,2]
[R=0,0,0,0]
[JOBS=4]

Solution encoding

A semiactive (no idle) schedule for a single machine typically consists of providing an order (sequence) in which the jobs are processed in the machine, i.e.

solution = [3,2,0,1]

Sample code

from scheptk.scheptk import SingleMachine

instance = SingleMachine('test_single.txt')
solution = [3,2,0,1]
print('Max. tardiness is {}'.format(instance.Tmax(solution)))
instance.print_schedule(solution, '..\\documentation\\images\\single_sample.png')

Parallel Machines

The ParallelMachines class serves to model a (identical) parallel machine scheduling problem. Each job has to be processed in one machine. This is the Gantt chart produced with the instance in the sample and the solution in the solution encoding section.

Attributes

Some of the Attributes are mandatory and produce an error if not found when loading the instance file. Others are optional, but they may produce errors in some cases if missing (e.g. if due dates are ommitted, then due-date related criteria cannot be computed).

• Mandatory:

• jobs - number of jobs
• machines - number of machines
• pt - processing times (a list containing the processing time of each job), which is the same in all machines

• Optional:

• w - weights. The weight of each job. If not specified, they are assumed to be 1.0
• r - release dates. The earliest starting time of each job. If not specified, they are assumed to be 0
• dd - due dates. The due date of each job. If not specified, they are assumed to be infinite

Instance

A typical instance is the following:

[PT=2,10,4,5,7,9,1,8]
[JOBS=8]
[MACHINES=3]

Solution encoding

There are several possibilites for encoding a solution. Perhaps the easiest is to provide an order (sequence) in which the jobs enter the system and assign the job to the machine according to the ECT (Earliest Completion Time) rule, i.e. the job is allocated to the machine that finishes first. Ties are broken according to the index of the machine, so machines with lower index have higher priority for the allocation.

solution = [1, 5, 6, 2, 3, 4, 7, 0]

Sample code

Unrelated machines

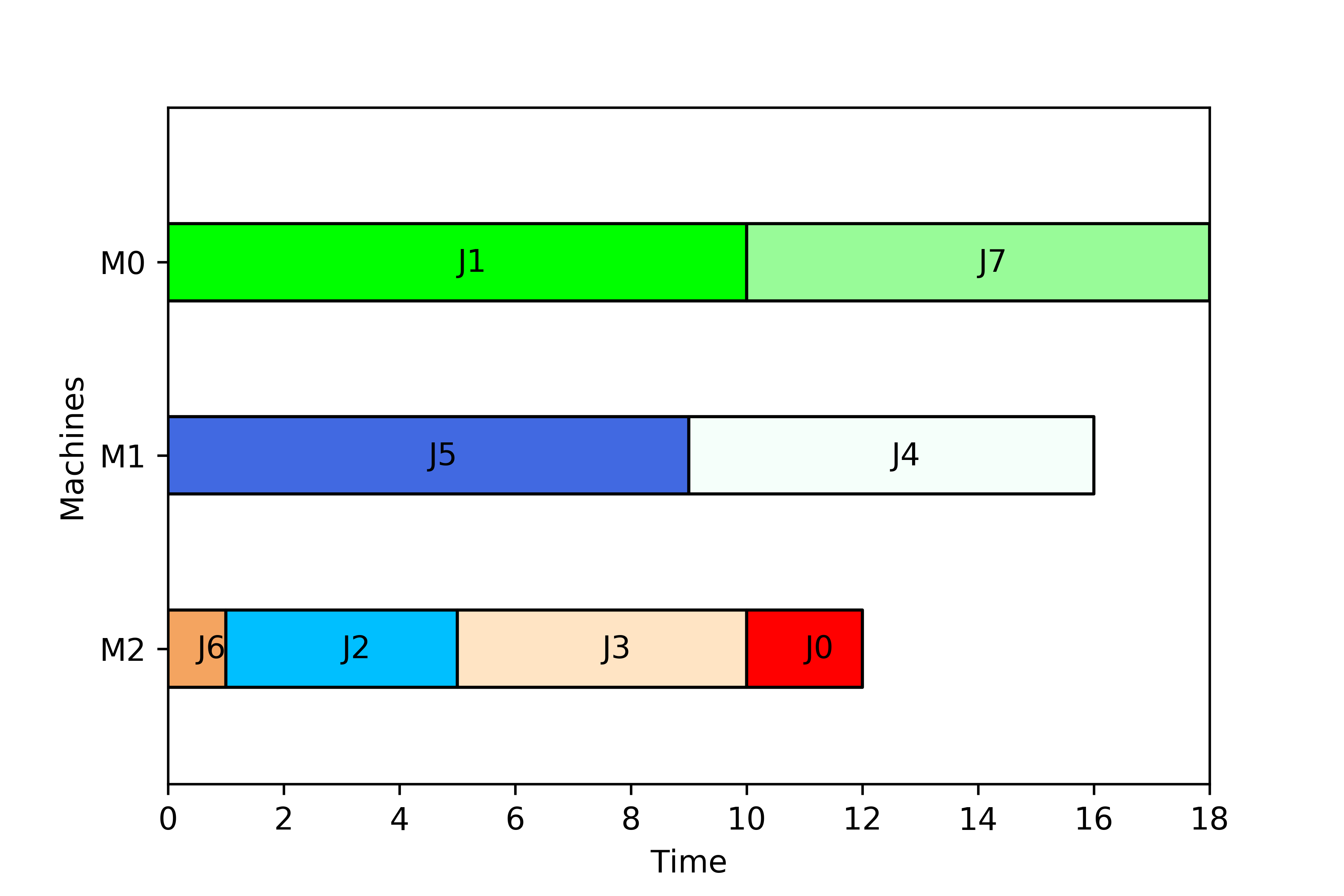
The UnrelatedMachines class serves to model parallel, but not identical machines. Each job has to be processed in one of these machines, but the processing times are machine-dependent. This is the Gantt chart produced with the instance in the sample and the solution in the solution encoding section.

Attributes

Some of the Attributes are mandatory and produce an error if not found when loading the instance file. Others are optional, but they may produce errors in some cases if missing (e.g. if due dates are ommitted, then due-date related criteria cannot be computed).

• Mandatory:

• jobs - number of jobs
• machines - number of machines
• pt - processing times of each job on each machine. It is a list of lists, i.e. a list containing the processing times of all jobs on the machine, so instance.pt[i][j] indicates the processing times of job j on machine i.

• Optional:

• w - weights. The weight of each job. If not specified, they are assumed to be 1.0
• r - release dates. The earliest starting time of each job. If not specified, they are assumed to be 0
• dd - due dates. The due date of each job. If not specified, they are assumed to be infinite

Instance

A typical instance is the following:

[JOBS=6]
[MACHINES=2]
[PT=5,13,5,2,8,6;9,12,10,4,3,10]

Solution encoding

There are several possibilites for encoding a solution. Perhaps the easiest is to provide an order (sequence) in which the jobs enter the system and assign the job to the machine according to the ECT (Earliest Completion Time) rule, i.e. the job is allocated to the machine that would first complete this job. Ties are broken according to the index of the machine, so machines with lower index have higher priority for the allocation.

solution = [5, 1, 4, 2, 3, 0]

Sample code

from scheptk.scheptk import UnrelatedMachines
instance = UnrelatedMachines('test_unrelated.txt')
sequence = [5, 1, 4, 2, 3, 0]
instance.print_schedule(sequence)
print(instance.Cj(sequence))

Flow Shop

The FlowShop class serves to model the permutation flowshop scheduling problem. Each job has to be processed in all machines in the same order. This is the Gantt chart produced with the instance in the sample and the solution in the solution encoding section.

Attributes

Some of the Attributes are mandatory and produce an error if not found when loading the instance file. Others are optional, but they may produce errors in some cases if missing (e.g. if due dates are ommitted, then due-date related criteria cannot be computed).

• Mandatory:

• jobs - number of jobs
• machines - number of machines
• pt - processing times of each job on each machine. It is a list of lists, i.e. a list containing the processing times of all jobs on the machine, so instance.pt[i][j] indicates the processing times of job j on machine i.

• Optional:

• w - weights. The weight of each job. If not specified, they are assumed to be 1.0
• r - release dates. The earliest starting time of each job. If not specified, they are assumed to be 0
• dd - due dates. The due date of each job. If not specified, they are assumed to be infinite

Instance

A typical instance is the following:

[JOBS=6]
[MACHINES=2]
[PT=5,13,5,2,8,6;9,12,10,4,3,10]

Solution encoding

A sequence indicating the order in which the jobs are going to be processed in all machines.

solution = [0,1,4,3,2]

Sample code

from scheptk.scheptk import FlowShop
instance = FlowShop('test_flowshop.txt')
sequence = [0,1,4,3,2]
instance.print_schedule(sequence)

makespan = instance.Cmax(sequence)

Job Shop

The JobShop class serves to model the jobshop scheduling problem. Each job has to be processed in all machines in an order given by a routing matrix. This is the Gantt chart produced with the instance in the sample and the solution in the solution encoding section.

Attributes

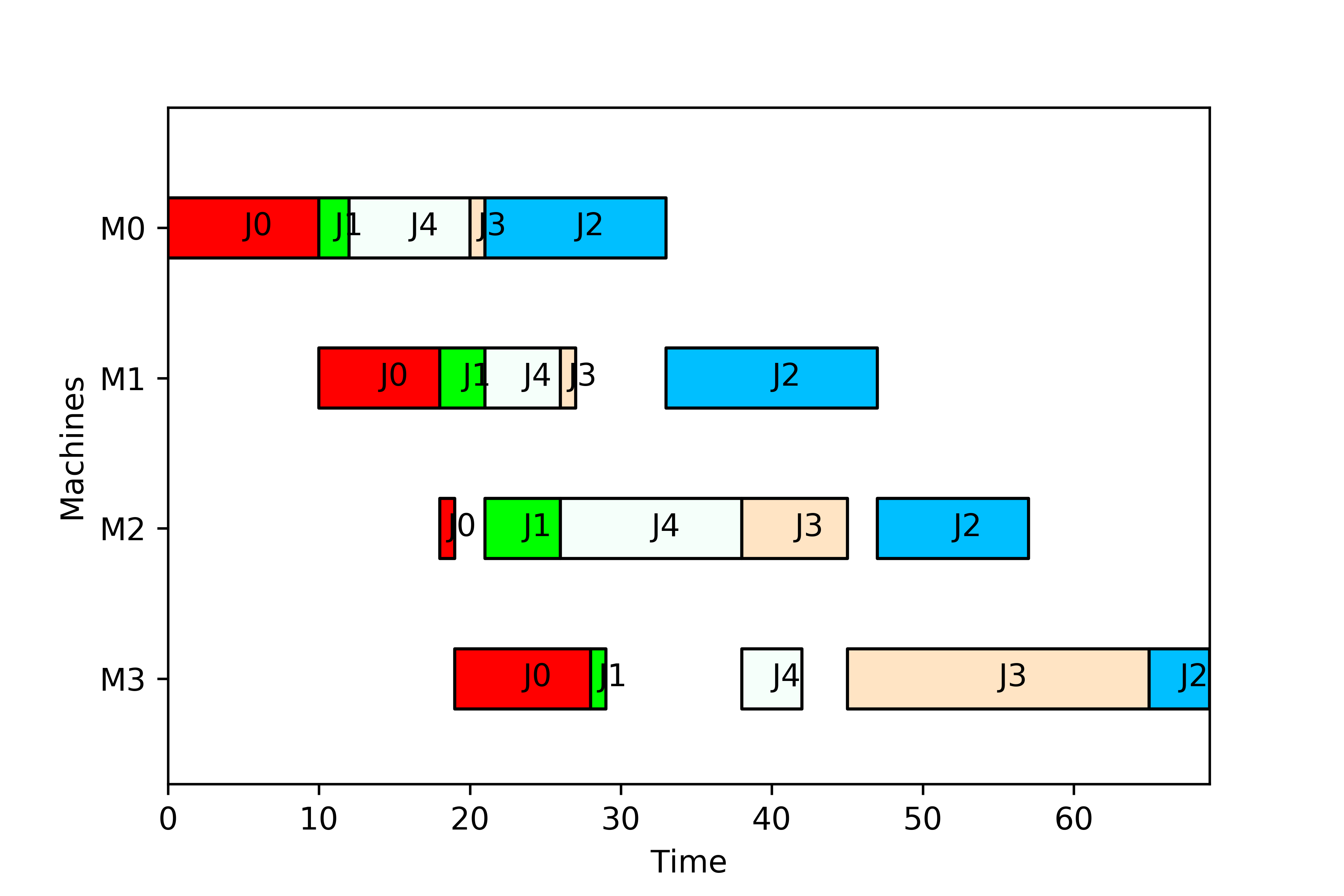
Some of the Attributes are mandatory and produce an error if not found when loading the instance file. Others are optional, but they may produce errors in some cases if missing (e.g. if due dates are ommitted, then due-date related criteria cannot be computed).

• Mandatory:

• jobs - number of jobs
• machines - number of machines
• pt - processing times of each job on each machine. It is a list of lists, i.e. a list containing the processing times of all jobs on the machine, so instance.pt[i][j] indicates the processing times of job j on machine i.
• rt - routing matrix. It is a list of lists, i.e. a list containing the routing of each jobs across the machines, so instance.rt[j] indicates the routing of job j, i.e. a list of the machines to be visited by the job so instance.rt[j][i] indicates the machine to be visited by job j in the i-th order.

• Optional:

• w - weights. The weight of each job. If not specified, they are assumed to be 1.0
• r - release dates. The earliest starting time of each job. If not specified, they are assumed to be 0
• dd - due dates. The due date of each job. If not specified, they are assumed to be infinite

Instance

A typical instance is the following:

[JOBS=5]
[MACHINES=4]
[PT=31,19,23,13,33;41,55,42,22,5;25,3,27,14,57;30,34,6,13,19]
[RT=0,1,2,3;3,1,0,2;2,0,1,3;1,3,2,0;3,0,2,1]
[DD=300,0,0,0,0]
[R=0,0,0,0,0]

Solution encoding

There are several possibilities for encoding a solution in a Job Shop. Perhaps the easiest is to provide an extended sequence where the jobs iteratively are assigned to the corresponding machine in their routing. solution =[4, 4, 3, 1, 1, 3, 1, 4, 1, 3, 2, 0, 4, 2, 2, 2, 0, 0, 0, 3] indicates that first job 4 is assigned to its first machine in its routing matrix, then job 4 is assigned to its second machine, then job 3 is assigned to its first machine, etc.

From version 0.1.3 on, the method get_sequence(solution) returns the order in which the jobs are processed machine corresponding to the solution solution, i.e. the value of job_order in following code (where test_jobshop.txt is the instance above) is [3, 1, 2, 0, 4].

from scheptk.scheptk import JobShop
instance = JobShop('test_jobshop.txt')
solution = [3, 3, 3, 3, 1, 2, 2, 0, 2, 1, 0, 0, 0, 4, 4, 4, 4, 2, 1, 1]       
job_order = instance.get_sequence(solution)

Sample code

from scheptk.scheptk import JobShop

instance = JobShop('test_jobshop.txt')
sol = [4, 4, 3, 1, 1, 3, 1, 4, 1, 3, 2, 0, 4, 2, 2, 2, 0, 0, 0, 3]
print(sol)
print('Cmax={}'.format(instance.Cmax(sol)))
print('SumCj={}'.format(instance.SumCj(sol)))
instance.write_schedule(sol, 'jobshop.sch')
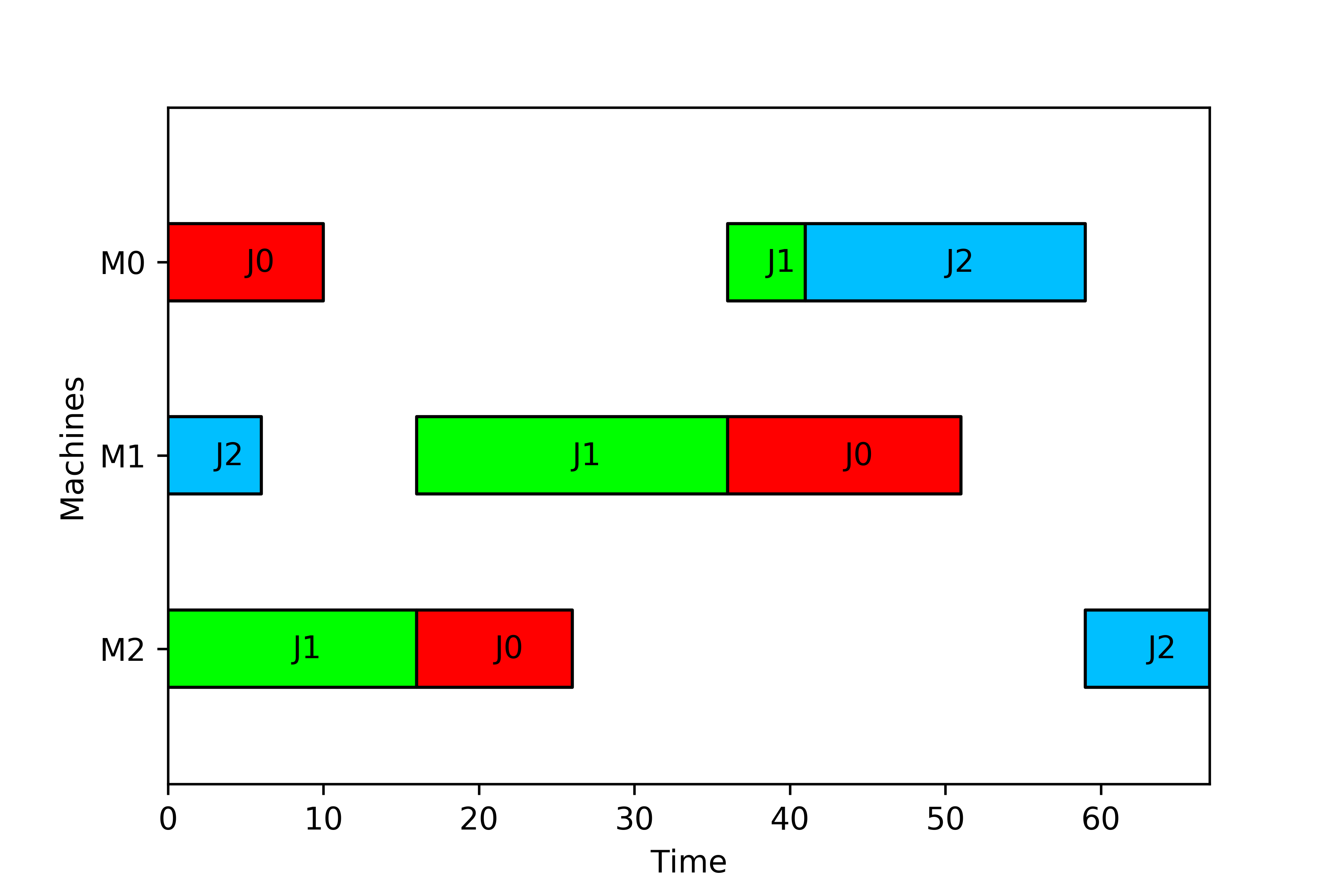
instance.print_schedule(sol, '..\\documentation\\images\\jobshop_sample.png')

Open Shop

The OpenShop class serves to model the open shop scheduling problem. Each job has to be processed in all machines in any order (no routing matrix). This is the Gantt chart produced with the instance in the sample and the solution in the solution encoding section.

Attributes

Some of the Attributes are mandatory and produce an error if not found when loading the instance file. Others are optional, but they may produce errors in some cases if missing (e.g. if due dates are ommitted, then due-date related criteria cannot be computed).

• Mandatory:

• jobs - number of jobs
• machines - number of machines
• pt - processing times of each job on each machine. It is a list of lists, i.e. a list containing the processing times of all jobs on the machine, so instance.pt[i][j] indicates the processing times of job j on machine i.

• Optional:

• w - weights. The weight of each job. If not specified, they are assumed to be 1.0
• r - release dates. The earliest starting time of each job. If not specified, they are assumed to be 0
• dd - due dates. The due date of each job. If not specified, they are assumed to be infinite

Instance

A typical instance is the following:

[JOBS=3]
[MACHINES=3]
[PT=10,5,18;15,20,6;10,16,8]

Solution encoding

Here it is used the so-called operations sequence solution encoding. Here it is an example of such encoding for a 3 job, 3 machine open shop instance:

Operation	0	1	2	3	4	5	6	7	8
Machine	0	0	0	1	1	1	2	2	2
Job	0	1	2	0	1	2	0	1	2

Therefore sol=[7,5,4,0,1,6,3,2,8] indicates that job 1 is first processed on machine 2, then job 2 is processed on machine 1, next job 1 is processed on machine 1, job 0 on machine 0 and so forth.

From version 0.1.3 on, several methods have been developed to ease handling the solutions:

• get_job(op): returns the job corresponding to the operation op, i.e. the value of job in following code (where test_openshop.txt is a 3-machine, 3-job instance) is 2.

  from scheptk.scheptk import OpenShop
  instance = OpenShop('test_openshop.txt')
  job = instance.get_job(5)

• get_machine(op): returns the machine corresponding to the operation op, i.e. the value of machine in following code (where test_openshop.txt is a 3-machine, 3-job instance) is 1.

  from scheptk.scheptk import OpenShop
  instance = OpenShop('test_openshop.txt')
  job = instance.get_machine(5)

• get_sequence(solution): returns the order in which the jobs are processed machine corresponding to the solution solution, i.e. the value of job_order in following code (where test_openshop.txt is a 3-machine, 3-job instance) is [1,2,0].

  from scheptk.scheptk import OpenShop
  instance = OpenShop('test_openshop.txt')
  solution = [7,5,4,0,1,6,3,2,8]       
  job_order = instance.get_sequence(solution)

Sample code

from scheptk.scheptk import OpenShop

instance = OpenShop('test_openshop.txt')
sol = [7,5,4,0,1,6,3,2,8]
print(sol)
print("Cmax={}".format(instance.Cmax(sol)))
instance.write_schedule(sol, 'openshop.sch')