-
Notifications
You must be signed in to change notification settings - Fork 1
Creating customised models
The models provided in scheptk are canonical models that do not include many constraints and objectives that may be found in real-life (such as setups, precedence constraints, or non-regular objectives). There are several functionalities in scheptk that allow you to create customised models with minimal effort, as well as solution procedures for these models.
In a nutshell, customised models are children of the Model class that carry out certain scheduling functions (e.g. which data to store and handle, how to compute the completion times, etc.) in an specific manner. So, in order to create a customised class, we should define the class as a children of the Model class and tell it how these specific funcions are carried out in this model.
Once these methods are described for the children class, all functions of scheptk should be available for the class. The following code summarises how a class Assembly_2_machines can be defined and used.
from scheptk.scheptk import Model
from scheptk.util import *
class Assembly_2_machines(Model):
# constructor of the class: define the data (temporary=attributes, persistent=tags in the file)
def __init__(self, filename):
self.jobs = read_tag(filename,'JOBS')
self.pt = read_tag(filename,'PT')
# computes the completion time of each job on each machine
def ct(self, solution):
# completion time of jobs on each machine (the two first machines are the first stage, the third is the assembly stage)
ct = [[0 for j in range(self.jobs)] for i in range(3)]
# earliest starting time on the machines (initially zero)
earliest_st_machine_1 = 0
earliest_st_machine_2 = 0
earliest_st_assembly = 0
for j,job in enumerate(solution):
# compute completion times of each job in the first stage
ct[0][j] = earliest_st_machine_1 + self.pt[0][job]
ct[1][j] = earliest_st_machine_2 + self.pt[1][job]
# compute completion time of each job in the assembly stage
ct[2][j] = max(earliest_st_assembly, max(ct[0][j], ct[1][j])) + self.pt[2][job]
# update earliest completion times of the machines in the stages
earliest_st_machine_1 = ct[0][j]
earliest_st_machine_2 = ct[1][j]
earliest_st_assembly = ct[2][j]
return ct, solutionOnce this code has been entered, all functions of a scheduling model in scheptk are available, i.e.:
instance = Assembly_2_machines('assembly_sample.txt')
solution = [1,0,2]
instance.Cmax(solution)
instance.SumCj(solution)
instance.print_schedule(solution)and the makespan, the sum of the completion times, or even the Gantt chart can be depicted. In the next sections, the details of this code are provided. We start by analyzing the Model class, discuss its different methods required to create the customised model, and provide one example. Then, we discuss issues related to solution encoding using another example.
Roughly speaking, a scheduling model is an abstraction of a real-life scheduling problem where the decision problem can be modelled using a set of data, constraints, and objectives (criteria). Data in a scheduling model can be stored in a persistent manner (i.e. a file or a database), or loaded in the computer memory while running the program (i.e. variables, or the attributes of a model class). Constraints in a scheduling model usually determine how the jobs are processed in the machines, therefore are implemented as methods of the model class. These constraints determine the value of certain magnitudes of interest (criteria), so the objectives are also methods of the class.
The Model class is the parent class of all scheduling models in scheptk. All scheduling models (e.g. SingleMachine, JobShop) are children classes of Model. Model already implements a lot of methods that are model-independent once we define which input data requires our model and how these data are going to be used to compute the completion times. Therefore, to create a customised scheduling model we only need to create a children class of Model (so all generic methods for Model are inherited and can be used in the customised model), and specify in this children class the two following methods:
-
__init__(filename). This is the constructor of the class, so each time an instance of the class is created, it executes this method. We will use this constructor to specify a filename with a set of corresponding tags that weill be stored into attributes of the class (for instance, the file may contain a tag namedJOBSthat will be loaded into an attribute namedjobs). The rules to write the constructor are described in detail here. -
ct(solution). In this method it is specified the manner in which the completion times for the jobs in a solution are computed on each machine. This is clearly model-dependent (it is not the same e.g. in a standard flowshop than in a no-idle flowshop), so it has to be specifically written for the customised model. The rules to writectare described in detail here.
As it has been mentioned above, __init__(filename) is the constructor where the data of the model are defined. Basically, in this function we will define what attributes would have the customised model, and what is the tag name that we will use to read them from a file. Typically, the __init(filename)__ will contain lines of code like the following one: self.attr= read_tag(filename,attr_tag) where attr is the name of the attribute (such as jobs, machines, setups, etc) and attr_tag is the corresponding tag in the file (such as 'JOBS', 'MACHINES', 'SETUPS', etc). In the example of the Assembly_2_machines class, the input file would read something like:
[JOBS=3]
[PT=40,4,8;21,14,25;16,5,12]
would require the following __init__(filename) method:
def __init__(self, filename):
self.jobs = read_tag(filename,'JOBS')
self.pt = read_tag(filename,'PT')Note that different tags could have been used for the model, for instance an input file like this:
[JOBS=3]
[PT_MACHINE_1=40,4,8]
[PT_MACHINE_2=21,14,25]
[PT_ASSEMBLY=16,5,12]
and the corresponding __init__(filename) method would be
def __init__(self, filename):
self.jobs = read_tag(filename,'JOBS')
self.pt = [read_tag(filename,'PT_MACHINE_1'), read_tag(filename,'PT_MACHINE_2'), read_tag(filename,'PT_ASSEMBLY')]which is certainly more visual although less simple. In any case, it is very important that the attribute processing times are stored in the standard way, i.e. self.pt[i][j] is a list containing, for each machine, the processing time of each job on this machine, or (in the case of a single machine) self.pt[j] is a list containing the processing time of each job. If this structure for the processing times is not followed, then it is likely that the functionalities related to the Gantt charts do not work properly. In this case, however, it is always possible to use the class Schedule to produce an ad-hoc chart as described here.
It is known from an earlier section that ct(solution) is a method that takes a solution (in a user-defined solution encoding) and returns the completion time of each job in the solution on each machine and the order in which the jobs are specified in ct. To lliustrate this, the code for the ct() method in the single machine case is included:
def ct(self,sequence):
completion_time = []
completion_time.append(self.r[sequence[0]] + self.pt[sequence[0]])
for i in range(1,len(sequence)):
completion_time.append(max(completion_time[i-1],self.r[sequence[i]]) + self.pt[sequence[i]])
return [completion_time], sequenceIt is important to remark that ct() returns a matrix (a list of lists) with as many rows as the number of machines, and as many columns as the number of jobs in the solution (not the total number of jobs). This difference is important for instance when one wants to deal with partial sequences (which represent partial solutions in many problems) and not with full sequences. This can be illustrated by the following example in the SingleMachine layout using the same 4-jobs instance that has been used to illustrate SingleMachine in another section of the wiki:
instance = SingleMachine('test_single.txt')
solution = [3,1]
completion_times, order_ct = instance.ct(solution)
print( 'Completion times: , completion_times )
print( 'Order of the jobs in the partial solution:', order_ct )The execution of this code provides the following output:
----- Reading SingleMachine instance data from file test_single.txt -------
[JOBS=4]
[PT=2,10,1,1]
[W=2.0,1,1,2]
[DD=11,13,13,14]
[R=0,0,0,0]
----- end of SingleMachine instance data from file test_single.txt -------
Completion times: [[1, 11]]
Order of the jobs in the partial solution: [3, 1]
As it can be seen, the completion_time list returned is composed of one element (one machine, a row), in turn composed of two elements (two jobs, the columns). It is not a one machine, four jobs matrix even if in the instance there are 4 jobs. Failing to return the completion times in this way might result in problems when calculating the indicators of partial measures.
A sensible question at this point is, Why the order of the jobs has to be returned by the function? Is not this information already known? This discussion is been addressed in detail here, and the answer is, in general, no, as there are encoding schemes (such as the codification used by JobShop or OpenShop) where the solution provided to ct() is not the sequence or order of the jobs. However, this is not the case if the solution encoding is simply the sequence of the jobs. However, since the methods related to Gantt charts are defined at the parent level (the Model class), then ct() has to be written always in the same way regardless the layout.
In the following we can see another example of the method ct() for the case of UnrelatedMachines:
# implementation of completion times for unrelated parallel machines (ECT rule)
# ties are broken with the lowest index
def ct(self, sequence):
# initializing completion times in the machines to zero
ct_machines = [0 for i in range(self.machines)]
ct = [[0 for j in range(len(sequence))] for i in range(self.machines)]
# assign all jobs
for j in range(len(sequence)):
# construct what completion times would be if the job is assigned to each machine
next_ct = [max(ct_machines[i],self.r[sequence[j]]) + self.pt[i][sequence[j]] for i in range(self.machines)]
# assign the job to the machine finishing first
index_machine = find_index_min(next_ct)
# increases the completion time of the corresponding machine (and sets the completion time of the job)
ct_machines[index_machine] = max(ct_machines[index_machine], self.r[sequence[j]]) + self.pt[index_machine][sequence[j]]
ct[index_machine][j] = ct_machines[index_machine]
return ct, sequenceAs it can be seen, the completion times returned include some zeros if the job is not processed in this machine. This is not a problem at all. Finally, please check the example of ct() for the JobShop() where it can be seen that the solution passed as argument is not the same thing that the list of the jobs:
def ct(self, solution):
# get the jobs involved in the solution in the order they are processed
jobs_involved = list(set(solution))
# completion times of jobs and machines
ct_jobs = [self.r[jobs_involved[j]] for j in range(len(jobs_involved))]
ct_machines = [0 for i in range(self.machines)]
# completion time of each job on each machine
ct = [[0 for j in range(len(jobs_involved))] for i in range(self.machines)]
# number of operations completed by each job (initially zero)
n_ops_jobs = [0 for j in range(len(jobs_involved))]
for job in solution:
# determine the corresponding machine
machine = self.rt[job][n_ops_jobs[jobs_involved.index(job)]]
# compute completion time
curr_completion_time = max(ct_jobs[jobs_involved.index(job)], ct_machines[machine]) + self.pt[machine][job]
# update completion times
ct_jobs[jobs_involved.index(job)] = curr_completion_time
ct_machines[machine] = curr_completion_time
ct[machine][jobs_involved.index(job)] = curr_completion_time
# update number of operations for the job
n_ops_jobs[jobs_involved.index(job)] += 1
return ct, jobs_involvedIn the previous model, the encoding of the solution was relatively straightforward (a sequence of jobs), so we could concentrate on building the method ct(). In the next example, we discuss how to model an unrelated parallel machine scheduling problem where we may want to use a different encoding: rather than a sequence of jobs plus the ECT rule employed in UnrelatedMachines, we would like to use a sequence of jobs per machine, i.e., for a 3-machine, 6-job instance, solution = [[0,2],[5,3,1],[4]] would indicate that jobs 0,2 are processed in the first machine (in this order), jobs 5,3,1 are processed in the second machine (in this order), and job 4 is processed in the third machine. To do so, we build the class UnrelatedMachineExtendedEncoding and develop the corresponding __init__() and ct() methods. The complete code is as follows:
from scheptk.scheptk import Model
from scheptk.util import read_tag
import sys
class UnrelatedExtendedEncoding(Model):
def __init__(self, file):
self.jobs = read_tag(file, 'JOBS')
self.machines = read_tag(file, 'MACHINES')
self.pt = read_tag(file, 'PT')
return
def check_encoding(self, solution):
if len(solution) != self.machines:
print('One sequence per machine must be given!')
sys.exit()
scheduled_jobs = []
for seq_machine in solution:
if len(seq_machine) == 0:
print('At least one machine does not have scheduled jobs!')
sys.exit()
else:
for job in seq_machine:
if job in scheduled_jobs:
print('At least one job is scheduled in more than one machine!')
sys.exit()
elif job < 0 or job > self.jobs-1:
print(f'Number of jobs in JOBS does not match the jobs indices: there is job index {job} whereas JOBS={self.jobs}!')
sys.exit()
else:
scheduled_jobs.append(job)
return True
def ct(self, solution):
self.check_encoding(solution)
job_order = [job for seq_machine in solution for job in seq_machine]
completion_times = [[0 for j in range(len(job_order))] for i in range(self.machines)]
for i, machine_seq in enumerate(solution):
for j, job in enumerate(machine_seq):
if j == 0:
completion_times[i][job_order.index(job)] = self.pt[i][job]
else:
completion_times[i][job_order.index(job)] = completion_times[i][job_order.index(machine_seq[j-1])] + self.pt[i][job]
return completion_times, job_order
As it can be seen in __init__(), in this case, we have not considered due dates, release dates, o weights in order to keep the code simple. Therefore, only tags JOBS, MACHINES and PT are considered (in PT, as usual, there are as many rows as machines, and as many columns as jobs, each position in the matrix containing the processing times of each job on each machine).
We have also coded an (optional) method check_encoding() to verify that the solution provided makes sense. Although this is not required, it is strongly recommended in order to avoid mistakes when testing the class. In our case, the function verifies that there is a list of jobs per machine, that the indices of the jobs are correct (no job with index less than zero or higher than the number of jobs minus one has been entered), that there is no machine without any job assigned (which, in general, does not make much sense), and that each job is assigned to only one machine.
Regarding the ct() method, after checking that the solution provided is correct, a job order is set by summing all jobs in the different sequences for the machines. Then, a completion time matrix is initialized to zero. Finally, in two nested loops, each job in each sequence of each machine is identified according to the job order previously obtained (if it is not the first job in the machine), and the completion times are updated accordingly by summing the completion time of the previous job processed in this machine if it is not the first job in the machine to the processing times of the job in the machine.
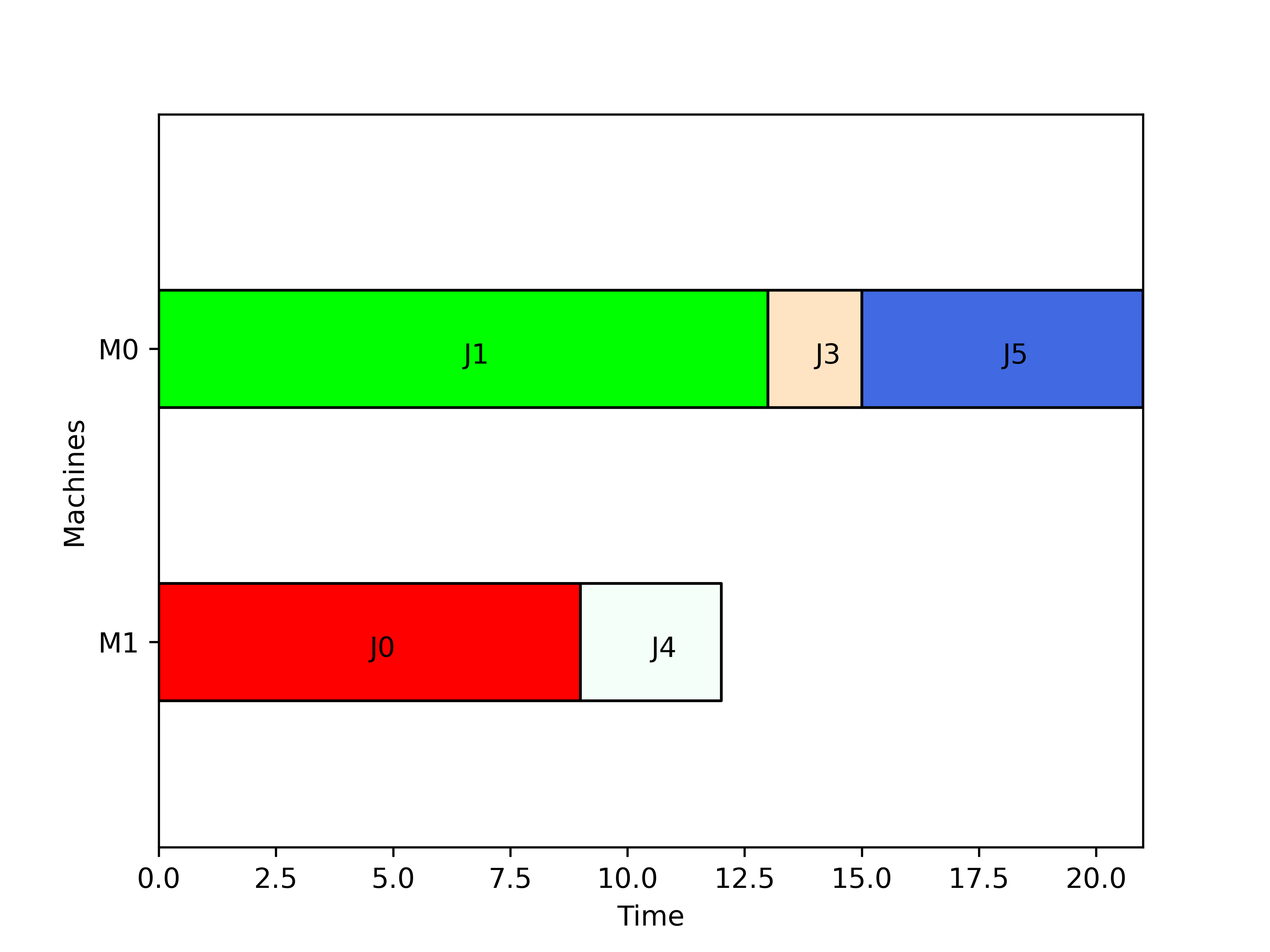
The usage of the customised model is presented in the following example (it is assumed that the definition of the class UnrelatedExtendedEncoding has been done somewhere else):
instance = UnrelatedExtendedEncoding('test_unrelated.txt')
solution = [[1,3,5],[0,4]]
print(instance.Cmax(solution))
instance.print_schedule(solution)and, for this file test_unrelated.txt:
[JOBS=6]
[MACHINES=2]
[PT=5,13,5,2,8,6;9,12,10,4,3,10]
yields a makespan of 21 and the following schedule: