Table Based Q Learning In Under 1KB

Introduction

Q-learning is an algorithm in which an agent interacts with its environment and collects rewards for taking desirable actions.

The simplest implementation of Q-learning is referred to as tabular or table-based Q-learning. There are tons of articles, tutorials, etc. already available on the web which describe Q-learning so I won't go into excruciating detail here. Instead, I want to show how efficiently table-base Q-learning can be done using tinymind. In this article, I will describe how tinymind implements Q-learning using C++ templates and fixed-point (Q-format) numbers as well as go thru the example in the repo.

The Maze Problem

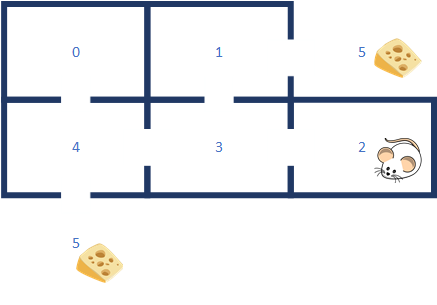
A common table-based Q-learning problem is to train a virtual mouse to find its way out of a maze to get the cheese (reward). Tinymind contains an example program which demonstrates how the Q-learning template library works.

In the example program, we define the maze:

/*
Q-Learning unit test. Learn the best path out of a simple maze.


5 == Outside the maze
________________________________________________
|                       |                       |
|                       |                       |
|           0           |          1             / 5
|                       |                       |
|____________/  ________|__/  __________________|_______________________
|                       |                       |                       |
|                       |                        /                      |
|           4           |          3            |           2           |
|                        /                      |                       |
|__/  __________________|_______________________|_______________________|
    5


The paths out of the maze:

0->4->5
0->4->3->1->5
1->5
1->3->4->5
2->3->1->5
2->3->4->5
3->1->5
3->4->5
4->5
4->3->1->5

We define all of our types in a common header so that we can separate the maze learner code from the training and file management code. I have done this so that we can measure the amount of code and data required for the Q-learner alone. The common header defines the maze as well as the type required to hold states and actions:

// 6 rooms and 6 actions
#define NUMBER_OF_STATES 6
#define NUMBER_OF_ACTIONS 6

typedef uint8_t state_t;
typedef uint8_t action_t;

We train the mouse by dropping it into a randomly-selected room (or on the outside of it where the cheese is). The mouse starts off by taking a random action from a list of available actions at each step. The mouse receives a reward only when he finds the cheese (e.g. makes it to position 5 outside the maze). If the mouse is dropped into position 5, he has to learn to stay there and not wander back into the maze.

Building The Example

Starting from cppnnml/examples/maze, I will create a directory to hold the executable file and build the example.

mkdir -p ~/maze
g++ -O3 -o ~/maze/maze maze.cpp mazelearner.cpp -I../../cpp

This builds the maze leaner example program and places the executable file at ~/maze. We can now cd into the directory where the executable file was generated and run the example program.

cd ~/maze
./maze

When the program finishes running, you'll see the last of the output messages, something like this:

take action 5
*** starting in state 3 ***
take action 4
take action 5
*** starting in state 2 ***
take action 3
take action 2
take action 3
take action 4
take action 5
*** starting in state 3 ***
take action 4
take action 5
*** starting in state 5 ***
take action 5

Your messages may be slightly different since we're starting our mouse in a random room on every iteration. During example program execution, we save all mouse activity to files (maze_training.txt and maze_test.txt). Within the training file, the mouse takes random actions for the first 400 episodes and then the randomness is decreased from 100% random to 0% random for another 100 episodes. To see the first few training iterations you can do this:

head maze_training.txt

You should see something like this:

1,3,4,0,4,5,
4,5,
2,3,1,3,4,3,1,5,
5,5,
4,5,
1,5,
3,2,3,4,3,4,5,
0,4,0,4,0,4,0,4,5,
1,3,1,5,
5,4,0,4,3,1,3,1,5,

Again, your messages will look slightly different. The first number is the start state and every comma-separated value after that is the random movement of the mouse from room to room. Example: In the first line above we started in room 1, then moved to 3, then 4, then 0, then back to 4, then to 5. Since 5 is our goal state, we stopped. The reason this looks so erratic is for the first 400 iterations of training we make a random decision from our possible actions. Once we get to state 5, we get our reward and stop.

Visualizing Training And Testing

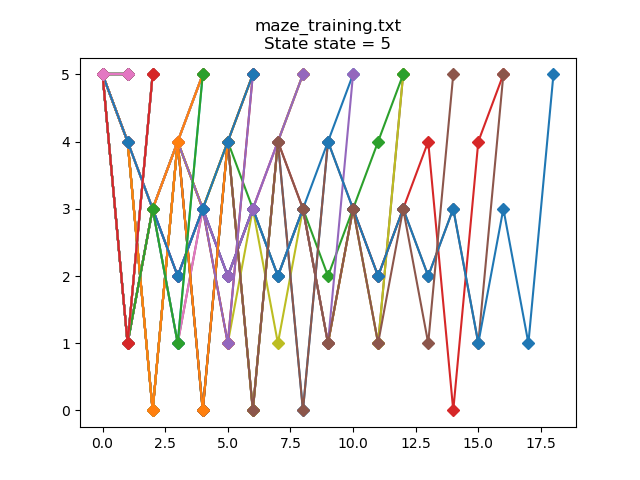
I have included a Python script to plot the training and test data. If we plot the training data for start state == 2 (i.e. the mouse is dropped into room 2 at the beginning):

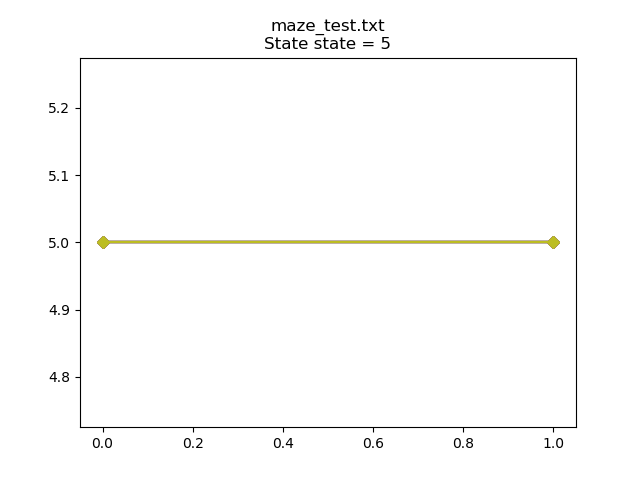
Each line on the graph represents an episode where we've randomly placed the mouse into room 2 at the start of the episode. You can see that in the worst case run, we took 32 random moves to find the goal state (state 5). This is because at each step, we're simply generating a random number to choose from the available actions (i.e. which room should be move to next). If we use the script to plot the testing data for start state == 2:

You can see that once trained, the Q-learner has learned, thru random experimentation, to follow an optimal path to the goal state: 2->3->4->5.

What happens when we drop the virtual mouse outside of the maze where the cheese is? If we plot the training data:

The mouse is making random decisions during training and so wanders back into the maze in most episodes. After training:

Our virtual mouse has learned to stay put and get the reward.

Determining The Size Of The Q-Learner

We can determine how much code and data are taken up by the Q-learner by compiling just the machine learner code and using the size:

g++ -c mazelearner.cpp -O3 -I../../cpp && mv mazelearner.o ~/maze/.
cd ~/maze
size mazelearner.o

The output you should see is:

   text    data     bss     dec     hex filename
    540       8     348     896     380 mazelearner.o

The total code + data footprint of the Q-learner is 896 bytes. This should allow a table-based Q-learning implementation to fit in any embedded system available today.

Conclusion

Table-based Q-learning can be done very efficiently using the capabilities provided within tinymind. We don't need floating point or fancy interpreted programming languages. One can instantiate a Q-learner using C++ templates and fixed point numbers. Clone the repo and try the example for yourself!