Quadcopter Exploration Project
This project serves 2 purposes. The first is to provide a PyDy template for creating quadcopter dynamics and outputing the relevant equations of motion.
The second purpose is to provide a simple working simulation of the quadcopter's dynamics and a simple controller that can handle position control and supports minimum snap (but also minimum velocity, acceleration and jerk) trajectory generation.
PyDy, short for Python Dynamics, is a tool kit made to enable the study of multibody dynamics. At it's core is the SymPy mechanics package, which provides an API for building models and generating the symbolic equations of motion for complex multibody systems.
In the PyDy Scripts folder, you will find multiple different scripts. Some express the drone's orientation in the NED frame, and some in the ENU frame.
NED frame : The world is oriented in such a way that the X direction is North, Y is East and Z is Down. The drone's orientation in this frame is front-right-down (frd). This is a conventional/classic frame used in aeronautics, and also the frame used for the PX4 multicopter controller.
ENU frame : The world is oriented in such a way that the X direction is East, Y is North and Z is Up. The drone's orientation in this frame is front-left-up (flu). This frame is widely used for its vizualizing simplicity (z is up), however it possesses a vizualizing complexity where "pitching up" actually results in a negative pitch angle.
The other difference in the provided scripts is that some use Euler angles phi (φ), theta (θ), psi (ψ) (roll, pitch, yaw) to describes the drone's orientation, while the other scripts uses a quaternion.
Euler angles : In the Euler angle scripts, the drone is first rotated about its Z axis by a certain yaw angle (heading), then about its new Y axis by a certain pitch angle (elevation) and then finaly about its new X axis by a certain roll angle (bank). The rotation order is thus a Body ZYX rotation. Using Euler angles, the resulting equations of motion possesses many sine and cosine functions, meaning that it requires more time to calculate. One must remember that these equations of motion are to be integrated in order to simulated the quadcopter's motion (using an ODE function for example). This means that the equations of motion are computed many time during a single timestep of the simulation.
Quaternion : The use of a quaternion to describe the drone's rotation significantly decreases computing time, because of the absence of sine and cosine functions in the equations of motion. The quaternion is formed with the angle value first, followed by the 3 axis values, like so : q = [q0, q1, q2, q3] = [qw, qx, qy, qz]. While it is sometimes complex to understand the rotation expressed by a quaternion, the quadcopter attitude control provided in this project uses quaternions (sets a desired quaternion, computes a quaternion error, ... ).
The quadcopter states are the following :
- Position (x, y, z)
- Rotation (φ, θ, ψ) or (q0, q1, q2, q3)
- Linear Velocity (x_dot, y_dot, z_dot)
- Angular Velocity (p, q, r) (The drone's angular velocity described in its own body frame, also known as Ω. This is not equivalent to phi_dot, theta_dot, psi_dot)
The PyDy scripts use the Kane Method to derive the system's equations and output a Mass Matrix (MM) and a right-hand-side vector (RHS). These outputs are used to obtain the state derivative vector s_dot in the equation MM*s_dot = RHS. To solve for s_dot, one must first calculate the inverse of the Mass Matrix, to be used in the equation s_dot = inv(MM)*RHS. Fortunately, for the quadcopter in this project, the Mass Matrix is a diagonal matrix and inverses quite easily. One can numerically solve for s_dot during the integration, but PyDy is able to analytically solve the state derivatives, which then can easily be copied into the ODE function.
Currently, I have seperated the PyDy scripts into 3 folders. The first is just a basic quadcopter. In the second, I have added gyroscopic precession of the rotors. And in the third, wind and aerodynamic drag was added.
NOTE: In my scripts, Motor 1 is the front left motor, and the rest are numbered clockwise. This is not really conventional, but is simple enough.
To be able to run the PyDy scripts of this project, you need to first install PyDy and its dependancies.
If you have the pip package manager installed you can simply type:
$ pip install pydy
Or if you have conda you can type:
$ conda install -c conda-forge pydy
First off, the world and body orientation can be switch between a NED or ENU frame in the config.py file. The other scripts then handle which equations to use, depending on the chosen orientation. It also has to be mentioned that both the PyDy scripts and the simulation aim to simulate the behaviour of a X configuration quadcopter (not a + configuration).
The only packages needed for the simulation part of this project are Numpy and Matplotlib.
In quad.py, I've defined a Quadcopter Class and its methods are relatively simple : initialize the quadcopter with various parameters and initial conditions, update the states, calculate the state derivatives, and calculate other useful information. The simulation uses a quaternion in the state vector to express the drone's rotation, and the state derivative vector is copied from the corresponding PyDy script. However, 8 other states were added to simulate each motors dynamics (2nd Order System) :
- Motor Angular Velocities (wM1, wM2, wM3, wM4)
- Motor Angular Acceleration (wdotM1, wdotM2, wdotM3, wdotM4)
The current parameters are set to roughly match the characteristics of a DJI F450 that I have in my lab, and the rotor thrust and torque coefficients have been measured.
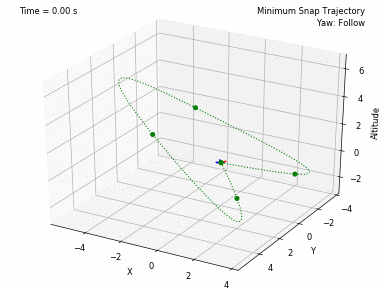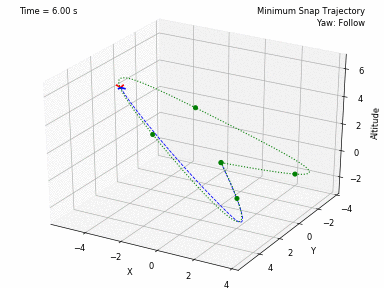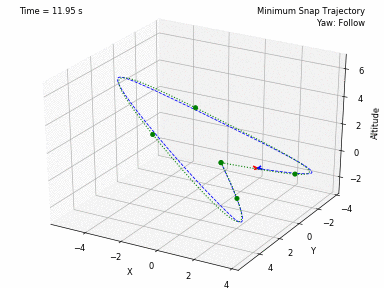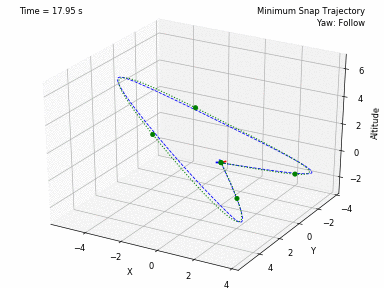
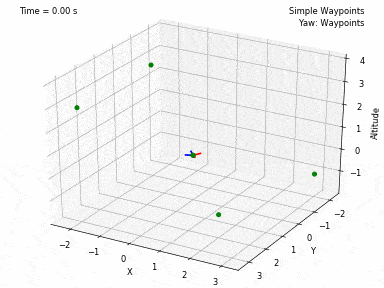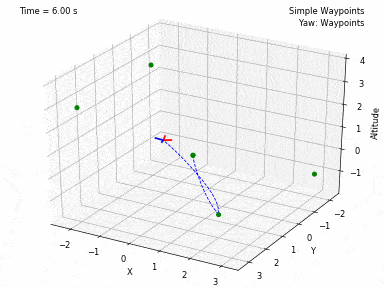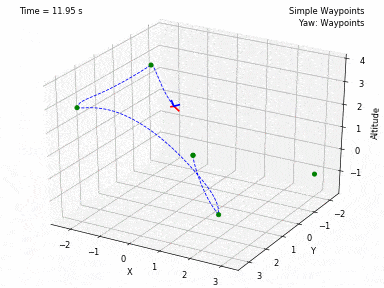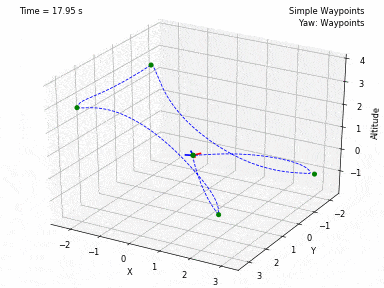
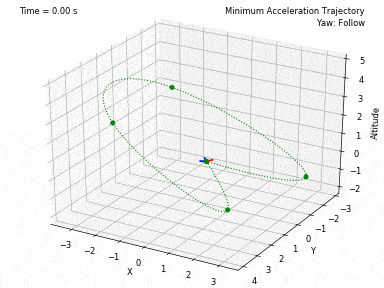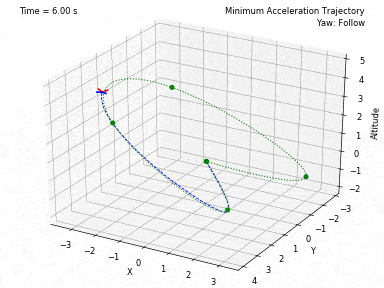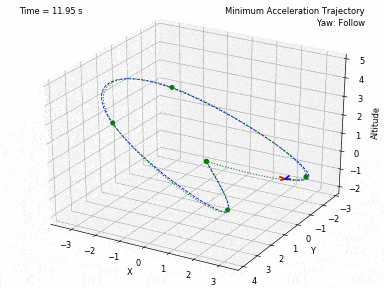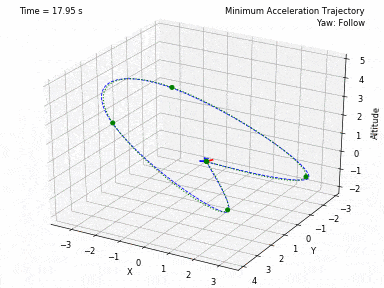
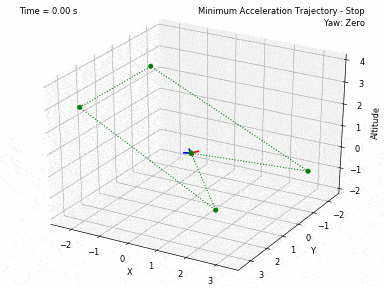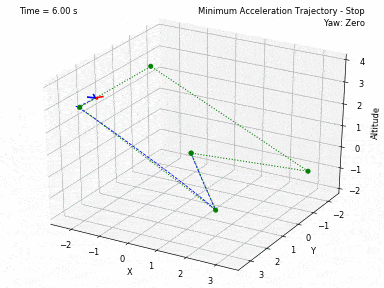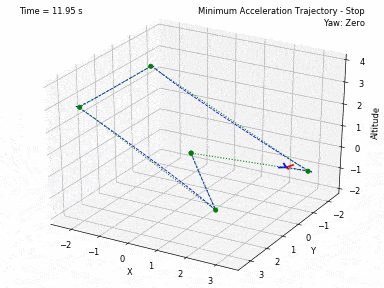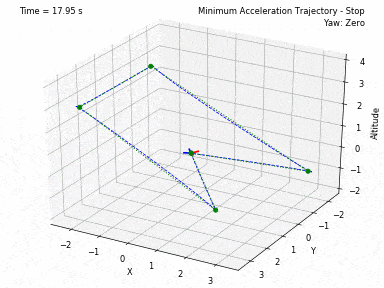
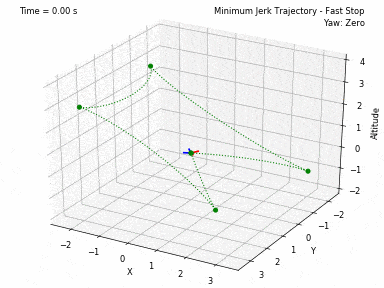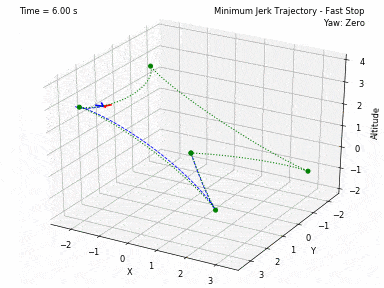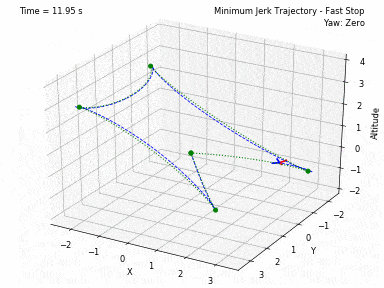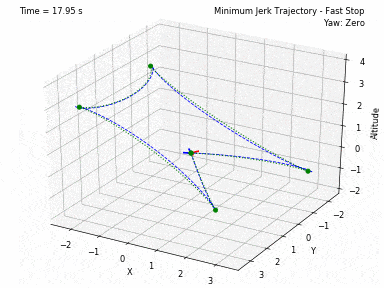
Different trajectories can be selected, for both position and heading. In waypoints.py, you can set the desired position and heading waypoints, and the time for each waypoint. You can select to use each waypoint as a step, or to interpolate between waypoints, or to generate a minimum velocity, acceleration, jerk or snap trajectory. Code from Peter Huang was modified to allow for these 4 types of trajectories and to allow for segments between waypoints of different durations. There is also the possibility to have the desired heading follow the direction of the desired velocity.
There are currently 3 controllers coded in this project. One to control XYZ positions, one to control XY velocities and Z position, and one to control XYZ velocities. In all 3 current controllers, it is also possible to set a Yaw angle (heading) setpoint. There are plans to add more ways of controlling the quadcopter.
The control algorithm is strongly inspired by the PX4 multicopter control algorithm. It is a cascade controller, where the position error (difference between the desired position and the current position) generates a velocity setpoint, the velocity error then creates a desired thrust magnitude and orientation, which is then interpreted as a desired rotation (expressed as a quaternion). The quaternion error then generates angular rate setpoints, which then creates desired moments. The states are controlled using a PID control. Position and Attitude control uses a simple Proportional (P) gain, while Velocity and Rate uses Proportional and Derivative (D) gains. Velocity also has an optional Integral (I) gain if wind is activated in the simulation.
There are multiple wind models implemented. One were the wind velocity, heading and elevation remain constant, one where they vary using a sine function, and one where they vary using a sine function with a random average value.
The mixer (not based from PX4) allows to find the exact RPM of each motor given the desired thrust magnitude and desired moments.
- PX4 "Position and Velocity Control" Source Code
- PX4 "Desired Thrust to Desired Attitude" Source Code
- PX4 "Attitude Control" Source Code --- Article
- PX4 "Rate Control" Source Code
- Minimum Snap Trajectory --- Article
- Add Perlin noise wind model
- Develop method to find gains for best response
- Add the possibility for more controllers (Attitude/Stabilize and Rate/Acro)
- Add scheduler to simulate and display animation in realtime simultaneously
- Simulate sensors and sensor noise, calculate states from sensor data (Maybe somehow running simultaneously? I'll have to figure out how.)